По первому закону Кирхгофа, Следовательно,

Свободные составляющие тока и напряжения определим как ] носги между полными й принужденными величинами:

вс №) = с (04 - с , (0.> - 60 - 75 = .25 В; 1. ад-1.(О.)- ..,(0ч.)=2-1,5=О.6 А;

4 (0.) -1, (0J -1 ,(0.) = 1 - О -1 А; f .(0.)-HOt)- ,№) = l -1.5=-0,5 А.

Так как свободный ток через емкость i=C~, то duc ]M ~

В рассматриваемом примере

(й Сс/Л)=с = (2Л0+)/С= 1/(100- Ю-в)=. 10* В/с.

Решение второй части задачи.

Характериспгческое уравнагаедяя п слекоммутащюнной схемы pRJiaC + Нз~ имеет одни корень

= -400 СК

КАЖДЫЙ ток равен сумме принуяг дшной составляющей и свободаой сост ляющей j4eP, где А ртно значению с

j ii/g-jf; бодной составляющей при tO (pCJ

8.19):

i (, = 1,5+0.5е- А; fg = e- А;

1з = 1,5 - 0,5е -w Л; с - 75 - гбе-мЙ

Рис. S.I9

Пример 82. В схеме рис. 8.20 до замыкания ключа был

вившийся режим: i?i= 2 Ом; coL = 3 Ом; в(/)= 127sm((of - 50°) I = 314 <г\

ТреЬуется: 1) найти i0+); 2) определить закон изменения в цепн после коммутации.

решение первей части аадачн. КоыадекскаА лмпятуда

тока в цепи до коммутации

-**-=25,4-аб°50 А

4+3/

Мгновенное значение тока до ксммутации

t = 25,4sin( -8650) А. в момент коммутации (при й1/ = 0)

i{OJf = 25.4sm(-в650) = -25,35 А. Принужденный ток после коммутации

2+3;

- = 35,2е->05°20-А,

Мгновенное значение принужденного тока

i p-35.2sm(ft)f-106W) А;

? p(0+) = 35,2sin(~10620)=-33,8 /Г.

По первому закону коммутации,

£(0 ) = i(0.) = -25,35 А.

Но /(0)-г р(0,)1;,(0Д Следовательно.

св(0.) = i (О,)- i p(0+) =-25,35 + 33,8 = 8,45 А,

Решение второй части задачи. Характзистическое уравнение pL-R ~0 имеет корень

По данным первой часта задачи, ток в цепв до коммутации (кривая / рис. 8.21 до ffi(=0)

i=2S,4sin(Mf-86°6C) А.

Мгновенное значение принужденного тока после коммутации (кривая 2 рис, 8.21)

.., = 35,2siii(<Bi-106°20) А; i (0J-M5 А.

Следователыю,

-4+( =35,2sin(( l- 106°20)-Ь8,45е- и А.

Кривая 3 рис. 8.21 определяет характер изменения-свободвого Юка, кривая полного тока посте коммутации (ординаты кривой 4 При и/55:0 равны сумме ординат кривых 2 и 3).

Пример 83. В схеме рис, 8.22 ключ замыкается в -гоетьей ветви. До этого был установпвгякйся режим; e{tt=El20 В Требуется ата; 1) (...(OJ; (Л ./<1(>.о.; UcM (ЙИс../<!0<= .; 2) i>(() и cJO.

Решение п рвой части задачи. До замыкания ключа

i(O-) = i,(0 ) = E/( ,+ J 120/(60+10) = 2 А.

Принужденный ток после коммутации i ,=i, ,=2 А. Поаотви ГОК через емкость ие проходит, поэтому is ,=0 ояинш

следаш , ИР *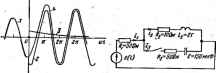

Рис. е.21

Рис. 8.22

Принужденное напряжение на емкости равно падению напряжения] на сопротивлении от тока i: пспр=2-10=20 В. По первому! закону коммутации,

2(0-) = ;,№)=2 А. Но i.(0,) = <..p(OJ + i .(0,), откуда

(04=<аО J - (00 = 2 - 2=0; i(0J-.-.(0J+b(OJ,

или

i,(0.) = 2+1.(04.

Составим уравнение по второму закону Кирхгофа дня замкнутого контура, образованного первой и третьей ветвями;

г (О.) fti + (04 ( з + с (04 = £. Так как Пс(04 = 0 и i,(04 = 2+i,(0J, то

50+50

Свободная составляющая

i. (04 = i. (Oi) -1,., (04 = 0,2 - О - 0.2 А. Чтобы определить Utci.(04. составим урйвненое для ( иставляющих по контуру, образованному первоА и второй

=0,2 А.

откуда

i (04 =

ш (04 R.+i (04 R.+ (04=0.

(04 Ri - h (04 s =. -0,2 50- 0=-10 в.

Но Uic-U-ff-. Слвюватешю,

(dlJdtli.e=Bi (0,Vi.= -10/2 = -5 A/c.

Свободное напряжение на емкости при i=0+ подсчитаем по вто-~ рому закону коммутации;

и<:(04 = и<:(04;

вс(О4=<:г,(04+вс (04: o=20+uc (04; - .

отсюда uccb(04 = -20 В.

Определим скррость изменения свободной составляющей напряжения на емкости при i=0. С этой целью воспользуемся тем, что

1з.а=С* . Следовательно,

fac ,Jdl)t.c, = (04/С=OAdSO 10 ) = 1333 В/с.

Решение второй части задачи. Характеристическое ура .

иение

p=i.C(R,+ ,)+p[C(R R.+R.R.+W+4+?.+R.=0 имеет два комплетсно-сатряженных корня:

42,1 + 15,2 С- н Pi=-42.-/15,2 (гЧ Поэтому еБободная составляющая должна быть взята в виде e-sm(fi(of+v),

где 6 = 42,1; <,= 15,2; А в v определяют по значению свободной со-ставлтощей и ее перной производной при t = 0+. По данным первой части задачи,

(а р=2А; 1-2св(0+) = 0; i (0+) = -5 А/с; сч> = 20 В; ИссЛО+) = -20 В; йЬв (0.)= ВЗЗ В/с

Прн t = 0 e-*sin(tuo( + V) = sinv. Производная функций e-fisinKf+vi

- Лбе Psin ( й/ -(- V)+Ле-блю cos < /+v)i

Значение этой производной при /==0 равно

- 6А sinv + (йцЛ cos V.

Найдем значения Л н v для свободной составляющей тока ij. Для этого составим два уравнения:

за№+) = 0, или Л sinv = 0; Ёсв(0)=-5. или !-бЛsinv+ 0(cosv = -5, Совместное решение их дает v = 0 и Л =-0,328 А. Следсшателыю, я = Hp+ face = 2- 0,328е- . sin 15,2f А.

Кривая / рис. 8.23 выражает собой график t=f{f}. НаДдем А \ для своб<1циой сюставляковеБ напряженпи uci

С1н(0+) = -20, или >lsinv = -20;

Со,(0,)=1333, рли -6smv + cojcosv=I333.

Отсюда .4-S?,9 и v=-SIS?,!* КИМ образов,

ic- c.p+icu = 20-l-+ 37,9e-<- .isin(15,2i-31°52)B. Кривая 2 ис. 16.23 изобража

Пример 84. В схеме рис. 8.22 е([)л = I27sm(3I4(+40=)B. Параметры cmJ мы те же, что и в примере 83. До вкло чения ключа в схеме был установивший ся режим; Ц(;{0) = 0. Требуется найта; I) i, (Ot); (<fW<10. i).; uc (04 и (duc f<I(),.i ) У) и с(<)-Решение первой части задачи. До коммутации

ш = i .=-j=0,202е- > Д; 0,202 sin И - 4430);

i. (0->=ij (0)=ода sin (- 44°30) - - 0,1415 А.

Определим принужденные токн в напряжения ва емкости 1 оммутацив. Входное сопрошвление цепи

Рнс. 8.23

104.8е-< ИОм;

i =* /2 =. 127e V104,8e-/ - = l,213e A. Мгновенное значение принужденного тока после коммутации i P= 1,213 sin(a(-l-49°60); fut (О.) = 1,213 sin 49 50= 0,923 А. реЙ ег Р ! т параллельно соединенных второй я]

= 58,3е-/ э5 Q

Кошлсксное напряжение на параллельгом участке

0-1и.= 1 ЛЗеЛ -а>-.56,Зе- а5-68 2е< -и- В;

отсюда

/г = f= 68,2еВ-1 7(!0 + (628) = 0,1085е-<5 ; /г - OZ, 68,2ет- 7(60 - ,-21.3) = l,253e№- -. ]НгнОБенные значения принужденных токов ig и ig после коммутации: = 0,1085 sin (ю( - 58°45); = 1,253 sin (ш( -(- 6420); !npW=e.lM5sin(-58°4S)=-0,0928 А; 4 (0J = 1,253 sin 64 20= 1,016 А. Принулухенное напряжение на емкосга Oc,pm-/sm(-/,тС)=1,263е1 -и-.21,Зе-ло-=26,7е-№- В.

Мгновенное значение принужденного напряжения на емкости после воямутации

Ста = 26,7 sin (ш1-35°40); с , №)=26,7 sin (- 35Ч0-)=-15,57 В. По первому закону коммутации,

> > (0=(0J=- 0,1416 = (DJ + i (OJ; 4.,(0 ) = -0.0928 А; 0,1415+ 0,0928 - 0,0487 А. Свсдное напряжение на емкости Иссв(0+) найдем по второму вакону коммутации;

ис(0-)=ис.,№)+ с (0,); . .

а. (О.) =uc (04 - с, (0.)=О - (-15,57) = 15,57 В.

Для определения /эс.(0+) составим уравнегте по контуру, образованному первой и третьей ветвями:

\с (0.) . с (О J - 0. Заменим в нем ich(0.) на [-0,0487--1;кв(0ч)] н, учтя, что исо(0+)=а 15,57 В, получим:

...(0.)-i±i5i= 0,1314A:

i, (0.) = i . (0.) + (OJ -0,18 А.

Чтобы опр*У1елитъ Uit {04=L(dtgJdt)i=o, составим- уравнение для контура, офазованного первой и второй ветвями:

i..(0.)R. + .(OJR,+ i (0.)=0.

откуда

Kto(0J = 9,487 В; (*V,7<!0i -о, = 1 (0+)/t=9,487/2=4,74 А/с; (< c /<I0r-B,-fe.(Od/C =.-0,1314/(150. МН)=-87в В/с.