Ток через L не может изменяться скачком, но на нндуктивносга, равное L*-, скачкой измениться может. Это

противоречит второму зако: 10фкгофа.

Доказательство того, напряжение на емкости может изменяться скачю проводится аналогично. Обратимся к S) цепи с емкостью (рис. I

Составим для нее ураш . 8.3 по второму закону Кир]

где Е-э. д. с. источника, конечная величина; Нс.~напряжен1(( на емкости.

Так как jC-J-, то

Перед тем как приступить к изучению методов расчета переходных 1фОцесазЕ, необходимо условиться о некоторых дополнительных определениях.

§ 8.7. Начальные значения величии. Под начальными значениями величин (в литературе их называют еще начальными условиями) понимают значения токов и напряжений в схеме при ( = 0.

Как уже говорилось, токи через индуктивности и напряжения иа емкостях непосредственко после коммутации равны их значениям непосредственно до коммутации. Остальные величины: напряжения на индуктивностях, напряжения на активных сопротивлениях, токи через емкости, токи через активные сопротивления - могут изменяться скачком, и потому их значения после коммутации чаще всего оказываются не равными их значениям до коммутации.

Поэтому следует различать докоммутапионные и послекоммутацион-ные начальные значашя.

Дотммутаццонными начальными значениями называют значения токов и напряжений непосредственно до коммутации (при = 0-); послекоямутационными начальными значениями - значения токов и напояжений непосредстБенно после коммутации (при *0Д

Если допустип что напряжение с может измениться t то -* Со и левая часть (8.4) ие будет равна правой части!

Отсюда следует, что допущение о возможности скачкообразного нзм.-нения напряжения на емкости противсетагг второму закону Кнряп

Однако ток через емкость, равный С ~-, может изменяться с это не противоречит второму закону Кирхгофа.

Из указанных двух основных положений следуют два закон ] (правила) коммутации.

§ 8.5. Первый закон (правило) коммутации. Ток через индуктив-J ность непосредственно до коммутации it(0 ) равен току через ту ж-Г ицауктавиость непосредовенно после коммутации h (Oj:

Время (Ol представляет собой время непосредственно до j . мутации, ( - 0+ -после коммутации (рис. 8,3, 6). Равенство (8.5) i выражает собой первый закон коммутации.

§ 8.Р. Второй закон (правило) коммутации. Обозначим Hanpi ние на емкости наюсредсшенно до коммутации с (О-), а напряжа на ней непосредственно после коммутации с (О,).

В соответствии с невозможностыо скачка напряжения на (

(1с(0 ) = йс(04-Равенство (8.6) выражает собой второй закон коммутации.

§ 8.8. Независимые и зависимые (послековицтационные) начальные значения. Для любой схемы после ксяамутации в ней можно записать уравнения по законам Кирхгофа; нз этих уравнений определить значения токов во всех ветвях и напряжений на любых участках схемы в тюслекоммутационном режиме (при ( = 0+).

С этой целью значения токов в ветвях, содержшцих индуктивности, и значет1я напряжений на емкостях берут равными тем значениям, которые онн имели до коммутации при ( = 0-, а остальные токи и напряжения после ксвшутации при t = G+ находят из уравнений Кирхгофа, поскольку часть слагаемых в инх известна.

Значения токов чфез индуктивности и напряжений на екжостях, известные из докоммутащкяшого режима, условимся называть независимыми напольными значениями.

Значения остальных токов и напряжений при ( = 0+ в послеком-мутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, будем называть зависимыми нтальными значениями.

§ 8.9. Нулевые и ненулевые начальные условия. Если к началу переходного процесса HcnoqcraeHHO перед коммутацией все токи и все напряжения иа пассивных элшвдтах схемы равны нулю, то в схеме имеют место нулевые начальные условия. Если же к началу переходаого процесса хотя бы часть токов и напряжений в схше ч равны нулю, то в схше имеют место ненулевые начальные условия.

При нулевых начальных условиях токи в шцкгавностях и напряжения на емкостях начнут изменяться с нулевых значений, прн

нм!улевых условиях-с кк значений, KOToi je онн имели h I*s, сгвенно до кетшутации.

§ 8.10i Составление уравнений для свободных токов и янй. Для послсжоммутавдюнной схемы составляют урамения но нам Кирхгофа для полных токов н напряжений, так же как-делалось и раньше: скачала обозначают токи в веганх и произвол выбирают для них положительные направления, затем составл уравнения по первому второму законам Кирх<> Так, для схемы рис. 8, после выбега положил ных направлений для тс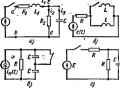

В этих уравнениях fa и ig - полные токи. К

р д . ДЫЙ из них состоит ИЗС1

бодного и пртгужденя токов. Для тою чтобы этой системы уравнений перейти к уравнениям для своОодегых ток. освободим систшу от вынуадающих э. д. с. (в нашем случае а. д. с. Е) н вместо ij запишем вместо - ig и т, д. Пол;

Заметим, что для тобого контура любой электрической цепи су падений напряжений от свободных составляющих токов равна ну,

} 8.11( Алгебраизация системы ]

i для свободных 1

в § 8.3 говорилось о том, что свободный ток прежтУБляет с £ ренкиие однородного дифференциального уравнения (уравнения ( правой части).

Как известно из курса математики, решение однородного дв ференцнального уравнения записывается в виде показательных фу.1 ций АеК Таким образом, уравнение для каждого свободного г..

можно представить в виде

1 =Ле

Постоянная интегрирования А для каждого свободного тока см Показатели же зат}хания р одинаковы для свободных токов г -Физически это объясняется тем, что вся цепь охвачена еданым ( переходным процессом.

Соаавнм 1фсязводную от свободного тсжа:

Оедовательно, щхнвврдную от свободного тока можно заменить иа р св. свободное напряжение на индуктивности L ~- - на Lpi Найдем ннтефал от свободного тока:

S di= S AtP = АЧр = Up.

Постоянная интегрирования взята здесь равной нулю, так как свободаые составляюшле не. содержат не завнсяищх от времени слагаемых.

Следовательно, интеграл от свободного тока можно заменить на UJp, а свсЛодное напряжение на емкости ~icdt - m 1 ЦСр).

В систему дифференциальных уравнений для свободных токов подставим Lpl вместо Ь- и вместо iadt. Получим:

(LiP -Ь Ri) tie. + tecBa = 0; (8.8)

Уравнения (8.8) представляют собой систему алгебраических уравнений относительно ам. зс в отличие от исходной системы не содержат прсжзводных и интегралов.

Переход от системы Л1шейных дифференциальных уравнений к системе алгеаических уравнений нг&ывакпалгебраиэацией системы диф ференциальных уравнений для свободных токов. Можно сказать, что система (8.8) есть результат алгебраизации системы дифференциальных >равнений (8.7).

§ 8.12. Составление характеристического уравнения снегам. Число алгебравческих уравнений равно числу неизвестных свободных токов. Положим, что р известно (в действительности оно пока ие найдено и будет определаю в дальнейшем) и решим систему (8.8) относительно и з(.в. Получим:

*Vb=VA; . Да/Д; е. =Да/А. где Д-определитель системы. В рассмотреннсш примере -I -1 LiP-Ri О

Сределнтель Д, получим из выражения для

путем замены первого столбца правой частью уравнений (8.8): О -I -1

определитель получим из выражения для А путем замены mopt столбца правой частью системы (8.8), н т. д.

Так как в правой части системы (8.8) находятся нули, то в каж определителе &i, и один из столбцов будет состоять из nyj

Известно, что если в определителе один из столбцов с .14 из нулей, то этот определшель равен нулю. Слещжатедьно, A, = i Д2 = 0; Дг-0.

Из физических соображений ясно, что каждый из свсЛодн j токов ие может быть равен нулю, ибо в этом случае не- буд выполнены законы коммутации. Однако нз предыдущего следует, ч 1 = 0/Д; iVb = 0/A; (з = 0/Д.

-Свободные токи могут быть ие равны нулю в-том случае, ил Офеделнтель системы

Д-0. (8.

При этом каждай из токов представляет собой неопределенн icB = Ai/A~0/0; ia,e = Дя/ДО/О; ... , раскрыв которую можно поЛ чить действительное значение каждого свободного тока.

Раскрытием неопределенностей заниматься не будем, а воспол зуемся тем существенным для дальнейшего выводом, что определитиш алгебраизированной системы )фавнений должен равняться нулю.

Уравнение Д = 0 называнхт характеристическим уравнением. Еди1 ственным неизвестным в нем является р.

Пример 75. Используя уравнение (8,8), составить характери. и ческое уравнение для схемы рис. 8.4, а и найтн его корни.

Решение.

lRitiC+p (flifeC+fc )+.+fia /ч рС -

Если дробь равна нулю, то равен нулю ее числитель. Следаш тельно,

p i?,LiC + p(RiR,C + Z.,)+i?i+i?, = 0. (8.1

Корни квадратного уравнения

В начале § 8.П говорилось о том, что решение для свободно! тока берегся в виде АеР. Если характеристическое уравнение И ---не один корень, а несколько, например п, то для каждого свобо. ного т(жа нужно взять

Пример 76. Найтн корни характеристического уравнения cx- d рис. 8.4, а -при трех значениях С: I) С=1 мкФ, 2) С = 10 мк 3) С = 100 мкФ, Ry = Rm Ом; LI Г.

Решение. При С=1 мкФ

адС +Li= 100-100-10- -4-1 = 1,01; 4(i?i-b2)2i-iC = 4-2G0-100-10 = 0,08: = 2 -100 -10- = 2 - Ю-*: 1.01 ±11.01-0.08. р 250с-ь р, = -9850 с- .

Pi.a = -

ПриС: При С

2.10-*

-10 мкФ pi = -230 с-*; Ра = -870 сЛ

= 100 мкФ р,-100+100/; Р2 = -100-100/.

§ 8.13. Составление тт

а уравнения путем исполь-

зования выражения для входного сопротивления цени на пкмен-иом токе. Характеристическое уравнение для огфеяелошя р часто составляют более простым способом, чем обсуждавшийся в предыдущем параграфе. С этой целью составляют выражение входного сопротивления двухполюсника на шремешюм токе [обозначим его Z(/(o)J, заменяют в нем /со на р [получают Z{p)\ и приравнивают Zip) нулю.

Уравнение Z(p) = 0 совпадает с характеристическим. Такой способ составления характеристического уравнения предполагает, что в схеме отсутствукя ыагнитносвязанные ветви. Если же магнитная свям. между ветвями имеется, то предварительно следует осуществить развязывание магнитносвязанных ветвей.

в 5 8.41 показано, что число р можно представки, в виде /Q, где fi-комплексная угловая частота; Z(p) есть сопротивление цепн на комплексной частоте. Сопротивление цепн для синусоидального тока частотой и, т. е. Z Ою). есге частный случай Z(p). когда fi=co.

Входное сифотавление на комплексной частоте по опкяыыпоо к некоторойй

I Zjb(p)=A(p)Mft(p), где Д (р)-определитель системы уравнений, с ных по методу контурных токов; (р)-алгебраическое дополнение.

Корни равнения Zt(p)=0 совпадают с корнями уравнении Д(р)=0. Следует иметь в виду, что во избежание погфн корни (корней) нельзя сокращать Д (р) и Дй(р) на общий множитель, если он имеется,

И последнее замечание: при составлении следует учитывать внутреннее

сопротивление источника питания.

Характеристическое уравнение можно составлять также, приняв за основу прн его сосгавленнн не метод контурных токов, а метод узлшых потен1№алов.

В этом случае следует приравнять нулю определитель матрицы узловых проаоди-мостей, полагая при составлении матрицы один из узлов схемы заземленным. Пример 77. Для Схемы рис. 8.4. а входное сопротивление относительно зажн-i пЬ при п

мов аЬ при переменном т

Заменим в нем /м на р и приравняем его нулю;