значение функции f{t) в соответствин с формулой (7,11) l/l + (mV2).

ilpHMqi 74. Разложить на составляющие функцию /(/) = 20(1-1-0,6sin 100sin

Решение,

<й-£2 = 99-103; o + fi= 101 10 ; тЛе/2 = е.

Следовательно,

/ (О = 20 sin lGt+ 6 cos (99 ЛЩ-В cos (101 1Щ.

Амплитуды колебаний боковых частот при АМ-колебании

ст глубины модуляции т, но не зависят от частоты модуляции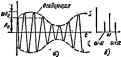

Ширина полосы частот, занимаемой АМ-колебаннем, не зависит от m н равна (o-ffi) -(ю -Й} = 2Й.

Рассмотрим спектры частотно-модулированных (ЧМ) в фазомодулирова (ФН) колебаний. Форма колебаний качественно покачана иа рис. 7.14, в.

Аргумент синусоидально изменяющейся функции / (() обозначим а (f), тогда

l{f)=Asmlaif)]. iaj

а <0 можно интерпретировать как угол, на который повернется вращающийся вектор иа комплексной плоскости за время L Угловая частота поворота этого вектора a=:da{t}[dt. В том случае, когаэ <в=сйв=с<я1$1,

Пря частотной модуляции частота а изменяется и равна При этом

Прн ф<0=амС/

Гаким образом.

йа{тйаС0=2 Ij W(v)йа(2п-Ь1)Ш;

cos а sin Ql)=Jo (Т)+2 S -и (Y) cos 2nQl.

Tut /ь(т)-бесселеза функция й-порядка от де*ствитеи.иого аргумента -р *.

Графики трех бесселевых функций пря *=0, 1. 2 изображены иа рнс, 7Д5. После преобразований

, (О/Л=Л (V) sin by,t+ Д <-l)V* (V) йа( ,-*Й)+(Г) йа 1. [в>

Теоретически полоса сги. Однако, если учесть, что с ростом k в равенстве (в) отбросить слагаемые рядов, амплитуды которых меньше 0,01, что имеет место при ky. 10 ЧМ-копебанне практи* чески занимает полосу частот

(ша -[- ftQ) - (шв-AQ) =2Ш 2yfi = =2<й<о/С).Й=2Д ).

Ширина ее зависит от глубины мадуля-цни Дм и ке зависит от частоты модуляции Й. Амплитуды боковых частот зависят ог До) и Q.

При фазовой модуляции угловая частота щ неизменна и меняется только фаза (О-Следовательно. а(0=Ш1+Ф(0. Приняв ])0=fmcosfi/. получим

/ (О =Л ЯП (иoг-ф COSU0-

занимаемых ЧМ-колебанием, равна бесконечйо-jfc (v) быстро уйеныиаегся, и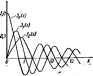

Амплитуда фазы ф от частоты модуляции Q ке а Опустии выкладки, найдем, что амплитуды боковых частот зависят от ф , а ширина полосы частот 2К1я=гф Й-от ф и Q.

§ 7.16. Расчет линейных цепей прн воздействии модулированных колебаний. Расчет токов н напряжений в лйнейных электрических цепях при ВОЗДЕЙСТВИИ на них модулированных колебаний производят либо для мгновенных значетий величин, либо для мгновенного значения огнйющея. В первом случае расчет проводят путем разложения модулированных колебаний на составляющие, расчета токов и напряжений от кандой нз них в отдельности и послед1чощего суммирования соответствующих токов н напряжений на основании принципа наложения. При этом ограничиваются теми составляющими, которые играют существенную роль в формировании выходной величины.

При воздействии амплитудно-модулированного колебания на какую-либо систему точный расчет огнбаюшрй выходной величины Может быть осуществлен по формуле интеграла Дюамеля для огн-

е для бесселевых функций приведено в § 15.14.

rtw t?!!!! P ? используют модулированные колебания н т* .i;?f..?*Ll . * ? . резонансные системы, разработай

е ветоды получения огибающей отклика :кскмТтт иных колебаний-<см.. например, ро]).

j. Изложите основные положения, нэ которых основывается методика расчета при периодических несннусондальных токах. 2. Охарактеризуйте;

физический смысл действующего отдельные слагаемые в формуле

4. Чем можно обуясннть, что ира

протекания тохов третьих гармоник неооднм нулевой провод? S. Охарактёпи-зуйте виды модулированных колебакий и занимаемые ими полосы частот 6 Решил, задачи 9.9; 9.12; бЛЗ; 9.15; 9.16; 9,19; 9,21; Э.25. 6.Р шч

шусондального тока. 3. Могут ли dBHoK мощности быть отрицательными? -нoй нагрузке трехфазной систе)

1га>ЕЮДНЫЕ процессы в линейных Э1№ри С1СИХ цепях

§ 8,1. Определение переходных процессов. Под переходными процессами понимают процессы перехода от одного режима работы электрической цепи (обычно перюдического) к другому (обычно также периодическому), чш-либо отличающемуся от предыдущего, наприлгер величиной амплитуды, фазы, формсй или частотой действующей Б схеме э. д. с, значениями параметров схемы, а также вследствие изма1ення конфигурации цели.

Периода1чесними режимами являн>тся режимы синусоидального и постоянного тока, а также режим отсутствия тока в ветвях цепй.

Переходные процессы вызываются коммутацией в цепи. Коммута-

-это процесс зачыкзния (рнс. 8.1, а) или размыкания (рис. 8.1, б] выключателей.

Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего докоммута-ционному режиму, к- энергетическому

.-------- состоянию, соответствующему после-

и) коммутационному режиму.

Рис. 8.1 Переходные процессы обычно яв-

ляются быстро протекающими; длительность их составляют десятые, шгые, а ино1да даже миллиардные доли секунды; сравнительно редко Длительность переходаых процессов достигает секунд и десятков секунд. Тем не менее изучение переходных процессов весьма важно, так как оно дает возможность установить, как деформируются по форме н амплитуде сигналы при прохождений их через усилители, фильтры и другае устройства, позволяет выявить превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока устаиовившшкя периодпчежся лршесса, а также олрепелвть продолжительность переходамо процесса.

§ 8.2. Приведение задачи о переходном процессе к решению линейного дифффенцналького уравнения с постоянными коэффициентами*. Запишем уравнение по второму закону Кирхгофа для схемы рис. 8.2 при замкнутом ключе. Сумма падений напряжения на индукпшности L и сопротивлении R равна э, д. с. Е: ut + RiE,

Lf+W=E. (ai)

Как известно из курса математики, уравнение, содержащее иеизвест-н)Ю функцию (в нашем случае i) и ее производные (в нашем случае

L)j называют диффсренциамным уравнением.

Таким образом, определение тока как ф>нкцни времени по сути дела есть решение дифференциального уравнения.

11звестно, что реикние диф(х;ренциального уравнения - это отыскание фупкщш, удовлетворяющей дифференциальному уравнен1ао. Под-стажжка этой функции и ее производных превра-щаег дифференциальное уравнение в тождество.

Решение линейных дафференинальных уравнений будем проводить в основном тремя методами: классическим, операторным и методом интеграла Дюамеля.

Перед тем как изучать эти методы, несходимо Рис. 8.2 рассмотреть общие свм*1ства линейных цепей прн переходных процессах, а также обшле законы, которым подчиняются п{(>ходные процессы в линейных электрических цепях. § 8.3 - 8.25 посвящены вопросам, имеющим отношение ко всем перечисленным методам расчета переходных процессов; однако часть этих параграфа (§ 8.3, 8.8, 8.10 н 8.12) следует рассматривать так же, как eeedenite к классическому методу расчета переходных процессов-

§ 8.3. Принужденные и свободные cocrai

: токов и напря-

жений. Ижесгао, что обшлй интеграл линейного дифференциального уравнения равен сумме частного решения неоднородного уравнения плюс общее решение однородного уравнения. Частное решение урав-ншия (8.1) равно E/R (£ -постоянная э. д. с).

Однородное уравнение получаем из исходного, если в нем возьмем правую часть равной нулю. В нашем случае

I.+W = 0. (8.2)

решением однородного уравнения является показательная функция вида ЛеР.

Для всех переходных процессов условимся, что момент г = 0 соответствует момеигу коммутации.

* Имеются в виду цепа с н

Постоянные А к р ке зависят от времени. Без вывода . их эначения для расематрнваемого примера: A=~~E/Rn p - RfM Следрватеяьвц решение уравнения (8.1) записывают так

(8.;

в нем слагаемое есть частное решение неодн01Х)дного

нения (8.1), а слагаемое--g -общее решение однородного уравН нения (8.2J. Подстановка (6.3) в (8.1) дает тождество

г, ~i

Следсеателыю, (8.3) денствтслыю является решетнем 5равне- ния (8.1).

Частное репюнве неоднсфодного дифференцналы10го уравненнй. будем называть принужденной составляюн1еЙ тока (напряжения),: а полное решение однороднее уравнения-гв(;б()5но составляющей.

Тик, нрименятсльно к рассмотренному примеру принужденная

составляющая тока равна E/R, а свободная составляющая-е

Полный ток = i p-bi(i-Кроме индексов пр (принужденный) я св> (свободный) токн и напряжения могут иметь и дсяюляигельные индексы, соответствующие номерам ветвей на схеме.

Т1рннужденная составляющая тока (напряжения) физически пред-ставлиет собой составляющую, изменяющуюся с той же частотой, что м дейстеующая в схеме принуждающая э. д. с. Так, если в схеме действует принуждающая синусоидальная э. д. с частоты ю, то принужденная составляющая любого тока и любого напряжения в схеме является соответственно синуссщдалышм током (а1нусондаль-. вым напряжением) частоты ы.

С1релел5вотся принужденные составляюнще в цепи синусоидального тока с помощью символического метода (см. гл. 3). Если в схеме действует источник постоаыной э. д. с. (как, например, в схеме рис. 8.2), то принужденный ток её* постоянный ток и находят его с помощью методов, рассмотренных в гл. 1.

Гкхтоянпый ток через емкость не проходит, поэашу пртшужден-пая составляющая тока через емкость в цепях с испяниками постоянной э. д. с. равна нулю. Кроме того, напаиним, что падение вапряжен}1я на пндуктианостн ог наеиеииого во временя тока равно; нулю.

в линшных электрических цепях свободные составляющие токов I, напряжений затухают во времени по показательному закону еС,

Так, в рассмотренясм примере =--e .

С увеличением времени t множитель е быстро уменьшается. Название свободная объясняется тем, что эта составляющая есть решен!1С уравнения. св(дного от вынуждающей силы (одноро;у1ого уравнсЕШЯ без правой части).

Из трех токов (полного, принужденного и свободного) и трех напряжений (полного, принужденного н свободного) основное значение имеют,полный ток и полное напряжение.

Полный ток является тем током, который в действительности гротекает по тон или иной ветви цепи при переходаом процессе. Его ыожпо изм(фить и записать на осциллограмме. Аналоп1чно, полное напряжение -это напряжение, которое в действительности имеется мелау некоторыми точками электрической цепи при переходном промессе. Его также можно измерить и записать на осциллограмме.

Принужденные и свободные составляющке токов н напряжений во время переходного процесса играют вспомогательнто роль; они ЯВ.-1НЮТСЯ теми расчетными кошюнентами, сумма которых дает действительные величины.

При любых п)еходных и установившихся процессах соблюдают два основных положения: ток через ивдуктивность н напряжение на емкости ие могут изменяться скачком *.

§ 8.4. Обоснование невозможности скачка тока через индуктивность n скачка напряжения на емкости. Доказательство того, что так через индуктивность не может изменяться скачком, проведем на примере схемы рис. 8.2. По второму закону Кирхгофа,

Ток I н э. д. с. Е могут принимать перечные (не бесконечно большие) значения.

Допустим, что ток I может нзмен1п-ься скачкш. Осачок тсжа означает, что за бесконечно малый интервал времени Ai-.-0 ток изменится на конечную величину Д/. При этом Д(/Д-.-со, Если вместо в уравнение (8.1) подставить со, то его левая часть не будет равна правой части я не будет выполнен второй закон Кирхгофа.

Следовательно, допущение о возможности скачкообразного измене-1Шй тока чдэез нндуктивносгь противоречит второму закону Кирхгофа,

Иногда эти положения формулируются так: потокосцепяетне ивдктивноЯ мтушкн и заряд конденсатора ммут изменяться только плавно, без скачков. Дальнейшее обо&ценне законов коммутации даио в § 8.28.