§ 7.13. Особенности работы трехфазных систем.

, 1фатными трем *. Электродвижущие силы каждой фцШ

трехфазного трансформатори или трехфазного генератора часто ока зываются несинусоидальными. Каждая э. д. с. (ед. £t) noBTojiMri no форме остальные со сдвигам на одну треть периода (T/Z) н мэж -г быть разложена иа гармоники. Постоянная составляющая оОычни отсутствует.

Пусть А-гармоннка э. д. с. фазы А

Так как э. д. с. фазы В отстает от э. д. с фазы А на Т/ЗН а э. д. с. фазы С опережает д. с. фазы А на Т/3, то ft-rapMOHiiKHJ э. д, с. в фазе Вив е С соответсТБсвно:

е : = Еш sin [Aw +1) + iJ*] = sin (ftorf + I20ft +Ч> );

Если ft = 1, 4, 7. 10. то А-гармоника э. д. с. фазы В отстает иа 120 от гармоники э.д. с. фазы Л. Следовательно, I, 4, 7, 10-я гармоники сйразуют систему пря- мой последовательности фаз (что понимают под прямой последовательностью фаз. см, в § 6.20).

Если ft = 2, 5. 8, П, то *-гарм01ижа э. д. с. фазы В опережает ft-гармонику фазы Л на 120 Следовательно. 2, 5, 8-я и т. д. гармоники образуют системы обратной по-следовательносп!.

Гармоники, кратные трем (fe = 3, 6. 9. образуют

систему нулевой последовательности, т. е. третьи гармо-7 7 НИКИ э. л. с. во всех трех фа-

зах совпадают по фазе (3-120= =360° :

ад=еав -вас = fsm sin {5<at +1,). Шестые гармоники э. д. с. также совпадают по фазе и т. д.

Совпадение по физе третьих гмоник э. д. с. во всех трех фазах прсяишюстрируем трафнчески.

.-Ji-iJ особенно теобяоднм студентам э.1ект1юэ11ергетнческнх я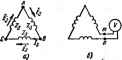

На рнс. 7.7 э. д. с. ел. <в. с представляют соЙой три ( э. Д. С- трехфаз1Юго генератора. Они имеют прямоугольную форму сдв У опюшенню друг к другу на одну треть периода основной частоты.

На том же рисунке показаны первая и третья гармоники казкдрА Э.Д.С. Из рисунка видно, что треты! гармоники э. д. с. действительно находятся s фазе.

Рассмотрим особенности работы трехфазных систем, вызываемые гармониками, кратными трем. 1. При соединении обмоток трехфазного генера- Ркс 7.8 тора (-фехфазного траис-

фсрматора) в треугольник (рис. 7.8.0) по ним протекают токи гар-ьюник. кратных трем, даже при отсутствии внешней нагрузки.

Алгебраическая сумма третьих гармоник э. д. с. в тртольникб равна 3£. Обозначим сопротивление обмотки каждой физы для третьей гармоники тогда ток третьей гарытши в треугольнике

аналопгчпо, ток шестой гармоники

UEjz

где /Те -дйствующее зиачение шестой гаркюники физноВ э.д. с; 2с -сопротивление фазы для шестой гармоники.

Действующее значе!ше тока. проккаюЩего по замкнутому треугольнику в схеме рис. 7.8. а.

генератора (трехфазного

2. Если соединить о&жлки трея, .....

трансфтматхфа) в открытый треугольник (рис. 7.8, б), то при наличии в фазных э. д. с. гармоник, кратных трем, на зажимах тип будет напряжение, равное сумме э. д. с. гармоник, кратных трем:

= ЗЕат sin{3coi-i-*,) -!-ЗЯ< sin (6cot -Ьтрв)

Показание вонвшетра в схеме рнс. 7.8, б

{/ = ЗКЯ+£+....

3. В линейнша напряжении независимо от того, в звезду или треугольник соединены обмотки генератора (трансформатора), Kpaj-. ные трем гармоники отсутствуют, если нагрузка равномерна.

Алгебраическан сумма первых гармоник э. д. с. и всех гармоник Э. Д. С, е кратных трем, равна нулю, поэтому от перечисленных гармоник при отсутствии нагрузки по замкнутому треугольнику ток протекать ме будет.

Рассмотрим сначала схему соединения -фехфамгого источника э. д. в треугольник (рис. 7.8, а) при отсутствии вншшен нагрузки, Обоэ начив Флз--потенциал точки А и фдз -потенциал точки В по трет-в гармонике, пачучим

Но Ea/gZa; следовательно, 41,3 = фвя. Прн наличии равномер ной нагрузки, соеданенной в треугольник, каждая фаза течерапзрЁ (трансформатора) и параллельно ей прно* единенная нагрузка могут быть заменены эквивалентной вегеью с некоторой э. д. с, £3 и сопротивлением Za. На полученную схш/ можно распространить вывод, сделанный дчя случая отсутствия внешней нафузки.

При соедЕшении в звезду трехфизного ис-

Р .,. точника э. д. с. (рис. 7.9) линейное напряже-

ние третьей гармоники равно разности соот-

ветствующих фазовых напряжений. Так как третьи гармоники в фазовых напряжениях совпадают по фазе, то при составлении этой разности они вычитанйся.

В фазовом нанряженнн могут присутствовать все гармоники (постоянная составляющая обычно отсутствует). Следовательно, дейсгеую-Щее значение физового напряжения

В линейном напряжении схемы рис. 7.9 отсутствуют гармоники, кратные трем; поэтому

и, -Уз vui+uffUi+::..

Отношение UjU<Yb, если есть гармоиико, кратные трем.

4. При соединении генератора н равномерной нагрузки в звезду и отсутствии нулевого провода токи третьих и других гармоник нулевой последовательности не могут протекать по линейным проводам. Поэтому между нулевыми точками приемника О н генератора-%) (рис, 7.10 при = оо) действует напряжение

Uo-o = Es sin (3(oi: + ij;a) + (wf-hae) + -..,

действующее значение которого

5. Если E схеме звезда -звезда при равномерной нагрузке физ сопротивление нагрузки для третьей гармоники обозначить Zhs, а сопрогавление нулевого провода для третьей гармоники - (рис. 7.10), 10 по нулевому проводу будет протекать ток третьей

гармоники

По каждому нз лннных проводов будет протекать ток третьей гармо* /ез/З.

AHajrarH4Ho нaxoдяt токи и других гармоник, кратных трем.

Пример 71* Мгновенное значение напряжения физы Л трехфазного генератфи

Ua = 127 sin (tot -1-100 + 30 sin (3(of -1-20*) -1- 20 sin 15 В.

Определить мгновенное значение линейного напряжения uab при соединении генератора в звезду.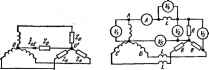

Решение. В линейном напряжении третья гармоника отсутствует.

Первые гармоники фаз Л и В по фазе сдвинуты на 120 . Поэтому линейное наприжение Uab первой гармоники в Уз раз больше фазо-вет-о напряжения первой гармоники Ол и на 30 опережает его по фазе.

Одиннадцатая гармоника (обратная последовательность фаз) линейного напряжения отстает по фазе от одиннадцатой гармоники напряжения фазы Л на 30° и раз больше ее:

Uab = 127УЪ sin (toi-h40 )201/3 sin (I Ш- 15 ) В.

Пример 72. Э.д. с, фазы Л в схеме рис, 7. И ед= 170 sin /-]> -Ь80собЗш/-1-34со89<оШ; R = 9 Ом; a>L = 2 Ом.

Опрелить показания всех приборов. Приборы электродинамической системы.

Решение. Действующие значения э.д.с

£j=I70/y2=l2IB: £з-55,5В: £в = 24,2В. По линейным проводам течет периая гармоника тока /1 = Ei/V+ W = 121/9,2 = 13,2 А.

* Эта формула получена путем составления уравнения по второму закону Кирхгофа для контура, оааованБого какой-либо фазой и нулевым проводом.

Рнс. 7.12

Показание вольтметра Vi равно УЩ+Ж+ЩШ В. Показание вольтметра равно 13,2-9= 118,5 В.

Показание вольшегра Vs равно /3-П8,5 = 20о В.

Показание вольтметра УГРк /L=26.4B. , ,

7f I J-\-7- Показание вольтметра равнч

Пр м 73. Э. д. с. каждой фа зы генератса (рис. 7.12) изменяетск по трапецеидальному закону: а = 220 В; а Т/36; нагрузка рав номерная; Ом; toL = 0,5 Ом-J

1/€)С=12 Ом.

Записать мгновжное значениеН тока по нулевому проводу, пре-1 небрегая гмониками тжа вышел седьмой. Г

Решение. С помощью табл. 7.1 записываем разложение трапб-i цвддальной э. д. с:

ел = (sin 10 sin (Of+ sin 30 sin 3wf + 18

+ i sin 50 sin 5ft>(-f 4sin 70 sin 7 (). Следовательно,

сд=274 sin ®f+89.3 sin Zat + 49,5 sin 5wf + 30,9 sin 7ю(. По нулевому проводу протекает только третья гармоника тока

где =89,3/12=63,3 В; Z = I,5j; Z s=6-4j;

2,3=2-/1,33; ;os=63,3/(1.5/+2-;l,33) = 31.8e- A. Мгновенное значение тока 1ад = 44,85(о{3 (~440) А.

§ 7.14 Биения. Колебательный процесс, получающийся в результате сложения двух синусоидальных колебаний с равными амплитудами А и близкими; но не равными частотами eii и (о, дает колебание, которое называют биением. Пусть f{t) = A sin 0j-iA sin Ogt.

Воспользуемся известным тригонометрическим преобразованием

sina+sinp = 2cossinifi. Следовательно, /(О можно представить следующим образом; /(0 = 2Л cos fi/sinraf.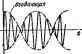

fi = (©i-<o,)/2. ю = (Ю1+ы,)/2 (fi<w).

График результирующего колебания изображен на рис. 7.ia Амплитуда колебания изменяегся по закону 2Лсо8£гл Огибающая колебаний нанесена пунктиром.

Возникновение биений при сложении двух синусоидальных колебаний с рав-кини амплитудамя и бчизкиый (но не раиыми) часготмш wcno-ibsyercH на практике в различных целях. - ------------ - ----- - -

ваемые колебания имеют И(

§ 7.15. Модулированные колебания. Прн передаче информации широко применяют модулированные колебания. Модулированным колебанием / (() = Л sin(cD/+) называкл-колебание, в котором амплитуда Л, частота ю, фаза If или и те и другие вместе изменяются во времени.

Колебание, в котором изменяется только амплитуда Л, а угловая частота ю и фаза ф неизменны, называют колебанием, модулированным по амплитуде.

Колебание с изменяющейся угловой частотой . но неизменными амплиту-

дой А н физой ф называют колебокпел,

модулированным по частоте.

Колебание, в котором изменяется только фаза if, а амплитуда А и угловая частота © неизменны, называют колебанием, модулированным по фазе.

Простейшим амплитудио-модулнрованным (AM) является колей-ние, в котором амплитуда модулирована по закону синуса: fit) = А (I +т Bin Qt) sin ( Г+ф).

где т -глубина модуляции (как праншю, т<1); fi -частота модуляции (fi<<o).

График AM колебания показан на рис, 7.14, а (огибающая дана пунктиром).

Если воспользоваться известным из тригонометрии тождеством

sinasinp = cos (а - р) i cos fa +р),

то колйЗзние Лo(+msinfi)sin(<l)+ф) можно представить в виде суммы трех колебаний:

/(0 = A,sin( .(+t)+cosf(<o-fi)f+t]

-cos[(<o+fi)i+ip].

Частоту й называют несущей, а частоты (o> - ii) и ((o + fi) -ftjKO-шми. Спектр АМ-колебання изображен на рис, 7.14,6. Действующее