§ l.II- Энгетвч

i баланс в электрических цепях. При про-

теканни токов по сопрогивлемгям в последшх выделяется тепло. На основании закона сохранения энергии количество теплоты, выделяк>- щееся в единицу времени в сопротивлениях схемы, должно радняться * энергап, доставляемой за то же время источниками питания.

Пслн направление тока /, протекающего через источник э. д. с. £. совпадает с направлением э. д. с, то источник э. д. с. доставляет в цепь энергию в единицу времени (мощность), равную EI, и произведение il входш с положительным знаком в уравнение энергетического баланса.

Если же направление тока / встречно направлению э. д. с. £, то источник э. д. с. ие поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и про-у-4ф д X взведение EI войдег в уравнение ~Л 5/eT~s я энергетического баланса с отрицательным знаком.

Уравнение энергетического баланса при питании только от источников э. д. с. имеет вид

Когдя схеме питается ие только от источников э. д, с, но н от источников тока, т. е, к отдельным узлам схемы подтекают и от них утекают токи источников тока, при оостав.1ения уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к узлу о схемы подтекает ток / от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UtU. Напряжение н токи вветвях схемы должны быть подсчитаны с учетом тока, подтекающего от источника Т1жа. Последнее проще всего еделать по методу узловых потенциале (см. § 1.22), Общий вид Уравнения энергетического баланса

Для практических расчетов электрических цепей разработаны методы, более зконшвчаые в смысле затраты времен и труда, чем метод расчета цепей по законам Кирхгофа. Рассмотрим этн методы.

§ I.I2. Метод пропорциональных величин. Согласно методу пропорциональных величин, в самой удаленной от источника э. д. с. ветви схемы (исходной ветви) провзвольно задаемся некоторым током, например током в 1 А. Далее, продвигаясь к входным зажимам тп. находим токи в ветвях и напряжения на различных участках схемы. В результате расчета получим значение напряжигая и щ схемы и токов в ветвях, если бы в исходной ветви протекал ток в I А.

Так как найденное значение напряжения в общем случае не бдег равно э, д. с. источника, то следует во всех ветвях изменил.

Ряс. 1.11

ТОКИ, умножив их иа коэффициент, равный отношению э. д. с. нсточ-иика к иаидешюму значению напряжения в начале схемы.

Метод пропорциональных величин, если рассматривать его обособленно от других методов, применим для расчета цепей, состоящих только из последовательно н параллельно соед(тенных сопротовлений и при наличии в схеме одного источника.

Однако этот метод можно использовать и совместно с другими методами (преобразование треугольника в звезду, метод наложения и т. вЛ, которые рассмотрены далее.

Пряиер 4. Найти токи в ветвях схемы рис. 1,П методом пропорциональных величин. Сопротивления схемы даиы в омах.

Решение. Задаемся током в ветви с ссщрсггивленпем 4 Ом, равным I А, и подсч1ггываем токи в остальных ветвях (числовые значения токов обведены на рисунке кружками). Напряжение ыещду точками тип равно I-44-3-3-f4-3 = 25B. Так как э, д. с. £ - ЮО Б, все токи следует умножить на коэффициент ft =100/25 = 4.

§ IAS. Методч£ОНтурных токов. При расчете методом контурных токов полагают, что в каждом незавмимсм контура схемы течет свой контурный ток. Уравнения сосгаяют относительно контурных токов, после чего определяют токи ветвей чр1)сз контурные токи.

Таким образом, метод контурных токов можно ОЕтределить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнении, которые необходимо было бы составить для схемы по второму закону Кирхгофа.

Слешэвателыю, метод контурных токов более экономен прн вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньшее число уравнений).

Вывод основных расчетных уравнений проведем применительно к - схеме рус. 1.12, в которой два

не;1ависимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток /и, а в правом (также по часовой стрелке) - контурный ток I- Для каждого из контуров составим уравнения по второму закову Кирхгофа. При этом учтем, что по смеж11ой ветви (с сопротивлением R) течет сверху вниз ток /ц/. Направления обхода ксжтзров примем также по часовой стрелке.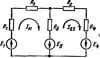

Для первого контура

(J?i+RJ/,i+R.(/u-/!!)=£i+E.

(а) (6)

(Я,+Я,+ВД / +(- .) / = £.+£.. Для второго контура

- Ип - + ( э + J = - Е, - Б. НЛИ г

(- *J Л.+(Ra+R.+ад - £. - Б,.

в уравнении (б) множитель при токе являющийся суммой сопротивлений первого контура, обозначим через множитель при токе (сопротивление смежион ветви, взятое со знаком минус) - через Ris.

Перепишем эти уравнения следующим образом: Зйесь .

где -полное или собственное сопрогавление nqieoro контура;

- сопротивление смежной ветви между педаым и вторым контурами, взятое со знаком минус; контурная э.дс. первого контура, равная алгебраической сумме э.д,с. этого контура (в нее со знаком плюс входет те э.д,с., направления котбрых совпадают с направлением обхода контура); Я - тлиж или собственное соЕфОпшление второго контура; -смтротивление смежной ветви между первым и вторым контурами, взятое со знаком минус; £22-контурная э.д.с. второго контура.

в й5щем случае можно сказать, что сопротивление смежной аетая между * и т контурами (fffcm) входит в уравнение со знаком минус, если направления контурных токов /йв и вдоль этой ветви вс1р*яны. н со знаком плюс, если направления втих токов согласны.

Ест в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:

или в матричной форме (см. § Б.З):

(1.4-)

Рекомищуется для единообразия в знаках сопротивлений с раз-вида индаяамв все контурные тот направлять в одну и ту же сторону, например все по часовой стрелке.

Если в результате решения системы уравнений какой-либо контурный ток окажется отрицательным, то это означает, что в действительности направление контурного тока офатно принято- му за положительное.

В ветвях, ие являющихся етежнымн между соседними контурами (например, в ветви с сопротивлениями Ri, схемы рис. 1.12), найденный контурный ток является истинным током. В смежных ветвях через контурные токи определяют истанные. Например, в ветаио сопрсггивлшиш Rb протекающий сверху внизЮк равен разности /ц -

Если в электритеаюй цепи имеется п независимых контуров, то число ураш1ший тоже равно п.

Общее решение системы п уравнений относительно тока таково:

UE+E +E :i-...+E,.. {1.6)

11 Ria Rla

Ri Rfi Ra Rw A= R - R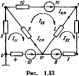

Rnl Rnt Rns Ran

(1.6)

-определитель системы.

Алгебраическое дополнение Л получаю из определителя А путем вычеркивания fc-ro столбца и т-й строки и умножения полученного определителя на (- 1)** *.

Если из левого верхнего угла определителя провести диагональ в его правый нижний угол (главная диагональ) и учесть, что R = = Rmk. то можно убедиться в том, что опредьтитель делится на две части, являющиеся зеркальным отображением одна другой. Это свойство определителя называют симметрией отноаапелыю главноИ диагонали. В силу симметрии определителя относительно главной диагонали Aft = A ft.

Пример 5. Найти токи в схеме рис. 1.13 с помощью метода контурных токот. Числовые значения сопротивлений и э.д.с. указаны на рисунке .

решение. Выбираем направления всех контурных токов /ц. и /ja по чховой стрелке.

Определяем: Ri = 5+5-\-4=H Ом; Ra2 = 5--104-2= 17 Ом; R2+2+l5 Ом; J? =J?si = -5 Ом; Rj2 = R==Q; n =R=. = -2 Ом; £ =-10 В; £=10 В; £ = -8.

Запишваем систему уравнений:

14/ -5/и -10; 6/ +17/г,-2/ -10;

-2/в + 5/ = -8.

Опрыелигель системы

14 -6 О -6 17 -2

0-2 6

= 100SL

Подсчитаем контурные токи:

10 -6 о 10 17 -2 8 2 6 -640 . ,.

-д--TooT-O-M*

/ =.0,224 А; / =-1.51 А.

Ток в ветви ш

=.=и-2!=-0.634 - 0,224=-0,86 А. Ток в вегеи от

..= >в-! =0,224+1,61 = 1,734 А.

Формула (1.5) в раде параграфов используется в качестве исход-вой при рассмотрении таких важных вопросов теории линейных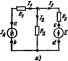

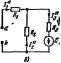электрических цепей, как определение входных и взаимных проводн-мостен вегеей, принцип взаимности, метод наложения и линейные соотношашя в электрических цепях.

Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками э,д.с. и сопротивлениимн, н что эти токи известны и равны токам соответствующих источников тока. Уравнения составляют лишь для контуров с неизвестными контурными токами. Если для схемы рис, 1.14, а принять, что контурный ток /,! = /* течет ссгласно направлению часовой стрелки

по первой и второй ветвям, а контурный ток /м=/з также по часовой стрелке по второй и третьей ветвям, то ссгласно методу кштурных токов получим только одно уравнение снеизвестным током

Отсюда /ва--:* и ток второй ветви h = Iu - f№

§ 1.14. Принцип наложения и метод наложения. Чтобы составить общее выражение для тока в -ветви сложной схемы, составим уравнения по методу контурных токов, вьгбрав контуры так, чтобы к-ветвь входила только в один fe-контур (это всегда возможно).

Тогда ток в й-ветви будет равен контурному току hk по уравнению (1.5). Киждое слагаемое правой часгя (1.5) представляет собой ток, вызванный в й-ветвн соответствующей контурной э.д.с, Наприм), Jii есть составляющая тока ft-ветвн, вызванная контурной э.д.с, £,1. Каждую из контурных эл.с. можно выразить через э.д.с. ветвей £i, £j, £3. ff. £ , сгруппнршатъ коэффициенты прн этих эс. и получить выражение следующего вида:

/fc = £igfti--£kfti+zg*s+..-. +Ebgkk+ ... -f-£ g*,. (1.7)

Если контуры выбраны таким образом, что какая-либо из э.д.с., например £ , входит только в один /п-контур и в другие контуры

не входит, то gtm - kJ.

уравнение (1.7) выражает собой принцип наложения.

Принцип наложения формулируется следующим образом: ток в k-еетви равен алгебрттской сумме токов, еызыеаемых каждой из 9.дх. схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей.

Принцип наложения используется в методе расчета, получившем название метода наложения.

При расчете црпей по методу наложения поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из Э.Д.С., мысленно удаляя остальные из схемы, во оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов. Заметим, что методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей как-чуммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока {P = RP).

Так, если через некоторое сопротивление R протекают согласно направпашые частичные токи /1 и /д, то выделяемая в нем мощность PRUi + lt) и не равна сумме мощностей от частичных токов: PфRI\ + m.

П{н1мер 6. Для схемы рис. 1,14, а с помощью метода наложения найти токи в ветвих, определить мощности, доставляемые в схему источником тока и источником э.д.с полагая ;?,=2 Oar, i?,=4 Or, J?3 = 6 Ом; h = 5 A; £ = 20 a