при расчете слодет учитывать, шо индуктивное сотротивленне X растет прямо пропорционачьно частоте. Поэтому для А-гармоники Xt в k раз больше, чем для первой гармсяшки Xi.

Xit = kaL = кХц1

Емкостное сопротивление уменьшается с ростом частоты, поэтому для -гармоники Xcft в йраз меньше, чем для первой гармоники Х:

Ха=1/(соС). /

Для каждой гармоники можно построить векторную диаграмму. Однако откладывать на векторной диаграмме токи и падения напряжения различных частот и тем более векторно складывать токи н падения напряжения различных частот иеддаустимо, поскольку угловые скорости вранюния векторов разных частот неодинаковы.

Активные сопротивления, если частоты не очень велики, полагают: от частоты не зависящими *.

При расчете каждую (армонику выряжают комплексным числом. Суммирование одаюименши гармоник производят путем сложения комплжсных чисел или векторэв на комплексной шюскосга, т. е. так же, как это делалось в гл. 3.

Пример 65. В левой ветви схемы рис. 7.4, а имеется источник тока iji(0=/*r,cos2<d/, в средней (второй) -источник э. д. с. е(0 = = En+E smb>t Индуктивность L магнитно связана с индуктивностью Lt. Взаимная ицоуктавность между ними М. Опрепелнп. нгшваиюе значение тсжа и напряжения на зажимах Дат: / = 5А; (0=1000 рад/с: £о=ЗВ; £ = 6 В; J?, = 30m; 1з = дгаГ; М = 1 мГ.

Решение. Положительные направления для токов выберем в соответсгвин с рис. 7.4. а. По второму закону Кирхгофа,

ио 40; поэтому Ut = -Mdialdt.

Воспользуемся принципом наложения и найдем составляющие тока (а ог кануюго источника в отдельности.

Схема ркс. 7.4, б служит для расчета токов ог действия постоянной составляющей э. д. с. Левая ветвь схемы разомкнута, так как в ней включен источник тока с бесконечным сопротивлением. Правая ветвь короткозамкнута, так как ищктивность для постоякного тока имеет нулевое ссч1рап1влеш(е. Прн этом ij = ER = I А.

Строго говоря, активное сопрогнвленне зависит от частоты вследствие явле-штя поверхностного эффекта. Явление поверяносиюго эффекта (см. ч. Ш учеб-тка) здесь не учитывается,

Первую гармонику тока i? находим, используя схему рис. 7.4. в: /S;.=6/(3-i-3/)=I.4le- .]

Вторую гармонику тока ii? находим в соответствии со схемой

рве.

7.4. г:

3+76 =

Мгновенное значение тока fg равно сумме мгновенных значений: 1ш + = 1 + 1,41 sin (©(-45)+23sin(2<i>f+2540 А. Напряжение

= М dydt = 1,41 cos ( I - 45 - 4,46 cos (2 i+2540) В.

§ 7.7* Резонансные явления пря несвнусоидальннх токах. Как известно из гл. 3, резонансным режимом работы электрическси! цепи.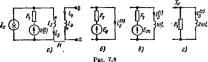

содержащей одну или несколько цндуктинностей н одну или несколько емкостей, называют такой режим ее работы, при котором так на входе этой цепи совпадает по фве с действующей на входе э. д. С.

Если действующая э. д. с. несннусашальна, то в элжтртческсй цепи могут возникать резонансные режимы (реэонансы тжов нЛй напряжений) не только на первой гармонике, но и на высших гар< мониках.

Услсшмся под резонансом на А-гармонике понимать такой режим работы, при котором тсж fc-гармоникн на входе цепи по фазе с(жпа-даег с й-гармоннкой, действующей на входе э, д. с. (но прн этом токи остальных гармоник не совпадают по фазе с вызвавшими их в. д. е.).

Если учитывать активные сопротивления индуктивных катушек, то условие возникновения резонанса для какой-либо гармоники заключается Б том. что реактппная состаоляющая входного сопротивления для этой, гармоники должна быть равна нулю.

Исследованке рсзонзнсн1>1х явленнй при иесинусоидальных токах часто производят, полагая активные сопротивления индуктивных катушек равными пулю. В этом случае входное сопротивление прн резонансе токов равно бесконечности, а входное сопротивление при резонансе напряжений равно нулю.

Ги возникновении резонансного и близкого к нему режима какой-либо высшей гармонике токи н (или) напряжения этой гармоники могут оказаться бблыиими, чем токи н Напряжения первой гармоники на этих участках цела, несмотря на то что амплитуда соответствующей высшей гармоники э. д. с. на входе схемы ножет быть в несколько раз меиыне амплитуды первой гармоники э. д. с, Пример 66. В схеме рис. 7.5 задана ин

дуктивность L. Полагая активное сопротив-Рвс. 7Л ленне индуктивной катушки равным нулю,

найти, при каких значениях емкостей Q и С> входное сопрспиБоенне схемы для первой гцмоники равняется нулю, а для девятой - бвзювечности.

Решение. Запишен выражоак д.тя входного сопропюлсиня схемы для первой гармоники и приравняем его нулю:

Приравняем бесконечности входное сопролтление для девятой га]я>юннкн:

Совместное решение дает

§ 7.8. Действующее значение весинусоидального тока н веси-иусондального напряжения. По определению (см. § 3.2), квадрат действующего значения тока / выражается через мгновенное згшчение тока i сле19чо1Цим образом:

Если ток

= +i~siii( !+il>,)+; sin(2ffli+*,)+ ... .

=5+2 1итЧШ+)+

5 Bm(pfflr+Ttv)sin(?(o(+Tl),)<i;=0. /-/8+4 + -%- + -%!-+... .

или .

Так как амплшуда А-гармбники тока в V2 раз больше деЙ-стшето знаяоиш irapMomiKH /ь то

Поэтому

2 V2 V2

(7. И)

Следовательно, действующее значение несинусондального тхжа равно корню нвадрапюму нз суммы квадратов постоянной составляющей т(жа и действуюищх значений отдельных гармоник. От углов CiiBHra фаз действующее значение тока не зависит.

Аналогично, действующее зиачение несинусмщального напряжения и разно корню квадраттюму из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник;

U = VUfW+VlTUff-. (7.II)

Пример 67. На входе двухполюсника и = 100 +80 sin (со/+ 30 ) + -f60sin(3iirf+20)+50sin(5a/-f-45)B; / = 33,3+17,87sin( (-18 )+ + 5,59 sin (5ш/ +120 ) А. Найти их действующие значения.

Решение.

t lOO+i + TTgl2r.l В: /=/33,3>+i

$ 7.fl. Средне п* модулю зваченне неамусмяадыяй фумщии. Под средним по яоЗ{/.1ю знакниеж функции понимают среднее значение модзля srolt функцав аа период

Jj-/(OiOI< -

В отличие от действующего эначення оно вавнсит о

(7.12)

значений

примера. Дана функций, не содержащая постоянной составляющей л чел яых гармоник и не изменяющая знака в течение каждого полупериода. Опредб лить ее среднее по модулю значение.

Решение. Разложим заданную функцию в ряд Фурье:

i=/x sm sin 8-ш(5©/+*б)+ ...

После интегрировании получим

§ 7.10 Величины, иа которые реагиитот ампч)метры и вольт метры при несинусоидальных токах* Несинусоидальные токи и иа пряжения измеряют приборами различных систем. Принципы действия этих приборов рассматривают в курсе электрических измерений. Поэтому здесь упомянем лишь, на какие величины реагируют вольтметры и амперметры различных систем.

Y f О

а) ё) 6) г) д) е) т 3)

Приборы элйстромагнитной, электродинамической н тепловой систем реагируют на действующее значение, магнитоэлектрические приборы с Быпримнтелем -на среднее по модулю значение величины, магнитоэлектрические без выпрямителя -на постоянную составляющую, амплитудные электротвые вольтметры -на максимальное значение функции.

Напомним, что

условный значок, свидетельствующий о том,к иакой системе относится данный прибор. На рнс. 7.6 приведены аексшчые нз низ: а-магнитоэлектрическая с подвижной рамкой.б-мапштоэлектрнческаясподанжныммагнятсп в-электро. магнитная, г-электродинамическая, б-ферродинамнческая, -тепловаа влектростЕтическая, з-магнитоэлектрическая с выпрямителем,

§ 7,11. Активная н полная мощности несинусоидального тока.

Под активной тяцностью Р несинусоидального тока понимают среднее значение мгновенной мо1даостн за период Нфв(* гармоники:

\ uidl.

Если представить напряжение и и ток i рядами Фурье: u = l/ +t/ sin(co(+$,)+t/ sin(2i.!+ + l/, sin(3m(+f,)+.,:l =о +ю sin И + *1 - q>i) +sin (2m(+Sf, - ,ГJ + + / sin(3ffl +t,-ir,)+ ...,

подставить эта ряды под знак интеграла и прсвштегрировать, учтя (дагиошения р. 10), то получим

Р = 1Л + адСО5ср,+адС051Й + ВДСО5Ч.,+ ... (7.14)

Таким образом, активная мощность Hecutit/coudaatHtKO тока роет сцмме акт11вных мощностей отдельных гармоник.

Полная мащашь S равна произвевепню действующего значения несииусоидапьного напряжения на действующее значение нееинусои-дальнего тока:

1де

пример 69* Найти jP н S, если

и=25,9 S m Ы -11°40) + 6 sin +ЪЬ%0) В; t=3sinH-40>-J-0,9V2siH(3o)i-i-I25°) А. Решение,

Ui = 2b,9{VJШ,г В; из-б/Уг =4,25 В; /;=2.13А; /а = 0,9А: ПЧО-(-40) = 2820; ч>з =-71П0; Р = 18,3 2,13cos 2820-i-4,25 0.9 cos (- 71Ч(У) = 35,5 Вт; U = VUl+Ul =V 18,3-1-4,26* =18.55 В; /-1/2,13-1-0,9=2,31 А; 5 = 1 - 18,55-2,31=42,8 ВА,

§ 7,12 Замена несинусоцдальвых токов н напряжений зквява-лентнымн синусоидальными. При изучении некоторых простейших свойств нелинетвлх электрических щ:пей (см. гл. 15) несннусоидаль-ные токи и напряжения, не содержащие постоянных составляющих, заменяют эквявалипнымя сннусоидальншш. Дейсгвукидее значение синусоидального кжа принимают равным действуюида1у значению заменяемого несикусшдального тока, а действующее аначение синусоидального напряжения -равным действующему значению несину-соцдального напряжшия.

Угол сдвига фаз между эквивалентными синусоидами напряжения и тока берут таким, чтобы актианая мощность эквивалентного синусоидального тока была равна активной мощности несннуооидаль-ного т(жа, т, е,

С05ф, = />/1 . (7.16)

Примф 70. Замтеить несивусоидальные ток и на1фяженне примера 69 жЕивалогтньшн синусщдапьными и найти угол сдвига фаз (ре между ними.

Решение. Действующее аначение синусоидального напряжения = 18,55 В; действующее значение шаусоцдадьного тока / = 2,31 А; cos = 35,5Д 18,55 2,31) = 0,828; ф, = 34