§ 7J2. ИзоСражение несинусовдал!

е юмощью рядов Фурье. Из курса математики известно, что л. периодическую функцию f{x) с периодом 2п, удовлегворнющую ус.Ц вням Дирихле *, можно разложить в рад Фурье.

Переменная величина х связана со временем t соотношением x = L}t = 2nt/T, где 7 - период функции во времени.

- Таким образом, период функции по х равен 2п. а период той 4нкцни по времени равен Т. Ряд Фурье записывают так:

fix)A + A[smx + AtSw2X{-AsSm3x-\-AlsiD4x-\-

+ AlcosX{-Aco52X{-AxCos3x-\-Alcos4x+ ... ,

где А - постоянная составляющая; Л; - амплитуда синусной няняцейся по закону синуса) составляющей первой гармоники; i амплитуда косинуснсй составляющей пе1жой гармоники; А - а. туда синусной составляющей второй гармоники и т. д. Здесь

A\ = -f(x)sidxdx: Л; = -1 j /(*) cosx d;

пУ <** sinkxdx; * = I f (л) cos kx dx. Так как

Л; sin fa:+Л* cos ftj; = Ил s in (ж + if),

A,V{W+iW и tg,==MfA TO рад Фурье (7.1) можно записать в пругой форме:

f(x)A + AySw(x + -,)+AsSmi2x-\rit-+ ,.. =

-A+i;sin{jtc+ifft),

(7.41

1де Ль - амплитуда Л-гармоннки рада Фурье,

Гармоники, для которых * -нечетное число, называют /четнышцЛ для которых k - четное число. - четными.

* Все периодические фуницня с которыми имеют дело в электротехи

унГд?£ Г?р я. Р° =Л Р -рку на выполи.

. § 7.3. Некоторые свойства псрнощческих кривых, обладающих симметрией. На рис, 7.1 и 7.2 изображены три кривые, обладакщие некоторыми специфичеащми свойствами.

Кривая рис. 7.1,0 удовлегеорнет условию я) =/(*).

Кривые, для которых Ьыполнимэ это условие, называют симмет-пичиыми относительно оси абсцисс. Если кривую рис. 7.1, о сместить по оси x на полпериодэ и зеркально отразить относительно оси х, та полученная кривая совпадет с кривой f{x).

При разложении таких кривых в рад Фурье отсутствуют постоянная составляющая и четные гармоники, т. е. равны нулю коэффициенты Ло = Ла = Лй=Л; = ЛГ= ... =0.

Пгатому кривые типа кривой рнс. 7.1. с раскладываются в рад

(д:) = Л;sinx--ЛГcosx--Л;sinЗд:--Л;cosЗд:- ...

Каждое слагаемое этого рвда удовлетворяет условию ~/{x+n) = = /(х). Так, например, - sin(j;-l-n) = sinjc.

Кривая, подобная кривой рис. 7.1,6, обладает симметрией отно ситедьно оси ординат и удовлетворяет условию fi-x) = fix).

Если кривую, лежащую левее оси ординат, зеркально отразить опюсителыю оси ординат, то получогная кривая совпадет с криюй, лежащей правее оси ординат. I рн разложениитаких кривых в ряд Фурье отсутствуют синусные (А\=А = Аз= ... =0)и присутстуют лишь косинусные составляншще и постоянная составляющая.

Таким образом, кривые типа кривой рнс 7.1,6 можно разложить в ряд

f (х) = Ло 4- Л; cos jt -Ь Л5 cos 2хА1соЪх+ ...

Кривые типа кривой рис. 7,2 удовлетворяют условию -f{~x) = fix); их называют кривыми, симметричными атоагтельно начала координат. Разложение их в рад Фурье имеет такой вцд:

/(л) = Л;sinл:+Лisin2л:+Л8SinЗл:-- ...

Рис, 7.2 .

§ 7.4. О разложении в ряд Фурье кривых геометрически пр*

внльной и неправильной форм. Встр(*чающиеся в аиектрогехнни периодические кривые можно подразделять на две группы:

I) кривые геометрически правилыюй формы, например трапедеч! дальней, треугольной, прямоугольной н т. п.; разложение их в р-( Фурье дано в табл. 7.1, где вместо х записано cof; 2) 1фивые прои 1 вольной (геометрически неправильной) формы; чаще всего они задаш в виде графика; разложение нх в ряд Фурье производят графичеси (графо-аналитически).

§ 7.5. Графический (графо-аналитический) метод определенн гармоник ряда Фурье, Графический метод определения гармоник рчг Фурье основан на замене опредеяенното интеграла суммой конечно числа слагаемых. С этой целью период фу1шции / (х), равный 2п разбивают на п равных частей Дх = 2п/п и интегралы э суммами.

По определению, постоянная составляющая

где р-текущий индекс, прит

1 до п; fpi)

... . . , . н значения ст . . -

аначение функщш f{x) при jc = (p -0,5)Дд;, т.е. в середше р-\ шпедвала.

Ашлитуда синусной составляющей й-гармсашки ряда >l*=f/(x)sinftj:d-2 M)sin,**.

амплитуда костпусвой сосгавляняч Д-гармонвкн

(7.-

Здесь smpkx и cos.fec -соответстаенно значения функций sin ft i и cosfer при x = {p - 6,b)tix, т. е, в середине р-го интервала.

При расчетах но формулам (7.5) -(7,7) обычно достаточно рааде-лить период на л ==24 или 18 частей, а в некоторых случаях н Н1 меньшее число частей.

/( 0=( in< +y sin M+ i sin5 (+ysln7B>/+...)

/ (to/) = sin о ЯП A. Bin Эх йп -Ь

/ W- (sin ol-i sin 3o(+ sin 5 (--isin7<.l+...)

f M=(sin-fi cos 01+1 Bin cos 3(.(+ + --.inc 6 ,+ ...)

/ M -~ + f COS и/+-г1з-COS 2 (--c ,to(+-jL. cos &.(-...)

+ -уП9--)

Перед тей Как производить графическое разложение в ряд, н < ходиыо выяснить, ие обладает ли раскладываемая функция снимет рией относительно осей координат (см, § 7.3). Наличие того или квота вида симметрии позволяет до проведения разложения предсказать, какие гармоники следует ожидать. Так, если кривая/(х) симмегрична относительно оси абсцисс, то постоянная составляющая и все четные гармоники отсутствуют, а вычисляя Л* н Л* при нечетных ft, следует учесть, что £/р(л:)Б1прЪ: за первый полуп р1Юд равна сумме 2fp{x)smpkx за втсдзон полупериод.

Знак углов ifft в формуле (7.4) зависит от знаков А% и Л*. При, построении гармоник иа общем графике необходимо учитывать, что масштаб по оси абсцисс для А-гармоннки должен быть взят в ft раз большим, чем для первой гармоники.

Так, например, если некоторый отрезок по оси абсцисс для пф-вой гармоники выражает собой угол п/3, то тот же отрезок для третьей гармоники выражает собой угол, в 3 раза больший, т. , 3 (л/3) = я.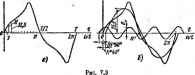

Пример 64. Найти первую и третью гармоники функции /(jt), изображенной на рис. 7.3, о. Значения ордннат функции fp{x) за первый полупериод при разбивке пер1юда на n = 24 части следуюшле: р ... I 2 3 4 5 6 7 8 9 10 II 12 fp(x) ...7 11 13.5 15,4 17,4 20,5 25.4 32.5 27,7 19,2 10 5

Решение. Так как 1фивая симметрична относительно оси абсцисс, то Ло = О и ряд будег состоять только из нечетных гармоник, Амплитуда синусной составляющей первой гармоники

л; - (7 sin 7=30 + 11 sin 22°30 + 13 sin 37°30 + 15,4 sin 52°30 + +17.4 sin 670- + 20,6sin8r30+26,4sin97°30+32.6sinll2°304-+ 27,7 sin J27°30 + 19.2 sin 142=30 +10sin I57°30 + +5sin 172°30) 25Д

Амплитуда ноошусной состааляюиъей пш щрноншш

;=4 2 f,Mcos,;t .-5,23. Ампли-Ода синусной составляющей третьей гармоники

Амплитуда косинусной составляющей третьей гармоники

0=1

Амплит1да первой гармоники Ai = y {A,f + {A,f =25,9. Тангено угла на который начало nejffiOH гармоники смещено по отношению к началу кривой f{x),

tg = ЛГ/Л; - 5,23;25,3 = 0,206; %=- 1140. Амплитуда третьей гармоники

Л,-У(ЛЭ +(Л;)> =6; 1е% = Л;/Л=1,47. 1}з = 5550. С1едовательно, если ограничиться третьей гармоникой, то /( О = 25,9sin ( £- 11-40) +6 sin (3©i-l-55°50).

На рис. 7.3,6 изображены пвая и третья гармоники полученного ряда, а также результирующая (суммарная) кривая. Ее можно сопоставить с кривой рис. 7.3, о.

§ 7.6. Расчет токов н i

ЙПрИ HCCRI

ииках питания. До проведения расчета вынуждающие силы (пж источника тока или э. д. с. источника э. д. с.) должны быть представлены рядами Фурье,

Согласно принципу наложения, мгновенное значение тока любой ветви схемы равно сумме мгновенных значений токов отдельных гармоник. Аналогично, мгновенное значение напряжения на любом участке схшы равно сумме мгновенных значений напряжений отдельны?; гармоник иа этом участке. Расчет производят для каждой нз гармоник в отдельности с помощью уже известных приемов.

Сначала рассчитывают токи и напряжения, возникающие от действия постояивой составляюЩЕй э. д. с. или исгочинка тока, после этого -токи и напряжения от действия пеЖой гармоники, затем от второй, третьей н т. д.

При расчете токов н напряжений, возникаюишх сгг действия постоянной составляющей э. д. с, необходимо иметь в виду, что падение напряжения на индуктивностн L при постоянном токе равно нулю, а также что постоянный ток чез емкость С не прохсщит.