тора на поворачивает его на угол 240° против часовой стрелка или, что то же самое, поворачивает его по часовой стрелке на 1]

С помощьй оператора а можно выразить э. д. с £ в и £с рнчной трехфазной системы через э, д. с. EaL

Ёв=аЁу. fc = E. (6..

§ 6.11. Соединение звезда - звезда без нулевого провода, рис. 6.8 представлена схема с двумя узлами (точки О и О).

расчета токов в ней целесообразно пользоваться методом двух узлс -(см. § 1.21). Напряжение между двумя узлами

--К.+Ув+Ус = Ул-Ув+Ус

Если нагрузка равномерна {YJ = Yв = Уc), то [см. соотношение

... ЁУС++дЧ

CoC--=0

и напряжение на каждой фазе нагрузки равно соответствующей э. д. с: Оао-Ёл Сво=Ёв, Осс - Ёс. Если нагрузка неравномерна, то Uo-oфО и

Г/ло = £ д -f/oo; Obo = Eb - Uoq; (Jco = Ec~Oo-o. Токи в фазах нагрузки:

Ia = Oao-!ZjC, h = OBo-IZB\ lc = Oco-lZc. Если в двух фазах нагрузка одинакова, например Zв = ZcфZA. то формула (6.7) после преобразований имеет следующий вил:

i преобразований имеет следующий вид:

(6.6)

§ 6.12. Трехфазные цепн при налнчии взанмоиндтации. Расчет трехфазных цепеи, содержащих шгнишосвязаяиые катушки пооиз-водится так же, как и расчет магавгаосвязанвых цепей ода<ЛаЬ,оп) сииуащдальнопэ тока.

Пример 63. Определить показания амперметра и вольтметра в схеме ил 6 16 Построить топографическую диаграмму, совместив ее с век-горной диаграммой токов. Дано: £4= 127 В; bL=1/ioC = 4 Ом; г М=2 0м.

Решение. Выберем положительные направления токов в соответствии с рис. 6.16, По первому закону Кирхгофа, />,-1-/в-1-/с = 0.

Примем э. д. с. Еа направлеиной по оси -j-1. Составим уравнение по второму закону Кирхтофа длй контура ОАОВО.

lj,i< L+hl4M - ОфЬ -Ь Л/шМ) = Ода. После подстановки числовых значений получим 2;(/>,-/а)-220еЯ0-.

llOe- А,

Для контура оауВО

-4 д-2/Л-4 я = 220/. Совместное решение трех уравнений дает:

?аИО; /в=110е/ -; /с= HOVeWiso* д.

Топографическая диаграмма, совмещенная с векторасй диаграммой токов, изображена на рис, 6.17. Амперметр показывает ПО А, вольтметр-приблизительно 640 В. Последний результат получен после подсчета фо- чо форм>ле

§ 6.13. Актнаная, реактивиая и полная мощности трехфазной системы. Под

активной моиюстью трехфаяюй сястшы понимают сумму активных мощностей фаз нагрузки и активной мощности в сопротивлении, включенном в нулшой провод:

Р = Ра + РвЛ-Рс+Ро- (6.9) Реоктивная мощность трехфазной системы представляет собой сумму реактивных мощностей фаз нагрузки и реактивной мощности в соврогивле-иьи, включенном в нулевой провод:

QQa+Qb-Qc+Qo- (6.10)

Полная мощность

s-Vp. . (6.11)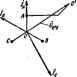

Ряс. 6.1Г

Если нагрузка равномерная, то

где фф-угол между напряжением на фазе нагрузки н током /, фазы нагрузки.

При рввиоыерной нагрузке фаз

е-ЗИффйП! ; {6,1

При равлоиерной нагрузке независимо иг способа се в треугольник

&озтГу вмо ф;7ьГ1бл S -b7j~iV=

нагрузке: /д-линейный ток нагрузка.

§6.14. Измерение активной мощности в трехфазной

Активная мощность системл равна сумме иоказаннй трех ветгаетров.

:.Для измерения!

нагрузка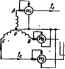

теутет, то нзмеренне мощности гроизвовят двумя I* Р - б-Э-показаний двух ваттметр<ГТвд оп?

деляет аяпгвную мощность всей системы иезавнсвмЬ от того/в звезду или т?

иТ.кГлГтзГз)* -

показание первого вагшетра равно R.Ojj BTopoTo-Re(?,1. Но

в ре55 тГт ° достаточно измерять мощность вдной из фаз-

§ 6.15. Круговые н линейные диаграммы в трехфазных цепях

Если меЕ1яется модуль сопротиплагая одной нз фаз трехфазной цепи, к, геоме1рическим местом концов вектсов напряжения (тока) любой из фаз чкп является окружность или прямая линия.

Для примера рассмотрим круговую диаграмму напряжений по схеме рис. 6.20, если Zb = Zc=/ = const и изменяется только модуль сопропшлёния фазы А (Zj,).

кгпользуем формулу заменив в ней индексы я н Ь на (У

к О. В режиме хачосгого кода ток по фазе А равен нулю, а наиря-ження на двух сопротивлениях g=Zc=-r равны £/вс/2-Точка О* в режиме х. х. находится посередине вектора Сцс (на рис, 6.21, о -точка /), при этом С/оОих = =-0,5£д. При коротком замыкании сопротнвленяя Za потенциал

комой окружное является разность .векторов (рис. 6.21, б) Uo0k.*-OOx., = Ea-(-0.5Ea) = = 1,5£ д. Для опредвлення входного сопротавлани? Z по отношению к точкам Л и О служит схема рис, 6,22, а (источники э. д. с. закорочены). Два сопротивления г включены параллельно, поэтому Z x=* = г/2 н р. = а

Рассмотрим три случая, отли>гающихся хгфактером сопротивлении Za.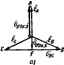

Рнс. 6.21

1. Когда Z - изменяющееся емкостное сопротивление, то => -i/u>C. ч> = -90 н 4)-v ~v -:-90. Круговая диаграмма напряжения I/q-o построена на рис, 6.22, б, где линия Хс проведена по отношению к хорде под углом - = 90°. Масштаб для Хс соответствует масштабу, в котором отрезок fd выражает входное сопротнв- ление Zbj = г/2. Геометрическим местом точки С является полуокружность fpA. Для определения величтшы и фазы Uo-o при некотором произвольном значении Хс его следует отложить на линии md и провести луч /т. Точка пересечения луча fm с полуокружностью fpA обозначена р. Напряжение Оо-о, соответствющее взятому значению Хс, изобразится вектором, проведенным нэ точки О в точку р.

2. Когда - изменяющееся ицдуктивное сопротивле11не,-го S? = и геометрическим местом концов вектора Uo-o является пояуокру, ность fgA (изображена пунктиром иа рис. 6.22, 6). Линия ного парамефа в этом случае будет справа от точки d.

3, Когда -чисто активное сопротнвляте, то ф==Фн -41 = и гюметрнческпм местом концов вектора С/о-о.является прямая А

§ 6.16. Указатель последовательности чередования фаз. Опредг ление порядка или поспеджательносги чередования фаз в трехйзн-И симметричной системе э. д. с. (напряжений) производят с помощ .Н указателя последжатеяьности чередования фаз. В простейшем испо нении он состоит из двух одиегзк Ч вых ламп накаливания и конленсо] тора (рнс. 6.23).

Емкость С берут такой величцЩ ны, чтобы емкостное сопротпвлашЩ 1/иС равнялось сопрогивлеиию к дон лампы. ,

Если три конца указателя по№ ключить к трем концам симметрач ной трехфазной системы э. я с-то потенциал нулевой точки cxei-a на рас. 6.23 будег определятьс положением точки О на векто]яюИ диаграмме рис. 6.22, 6 (соспветсТ вует точке р).

1!з диаграммы рнс. 6.22, б е . но, что напряжение на лампахЯ накаливания будет различно. Н* Г лампе, включенной в фазу Д, (шаЛ определяется вектором во-; над лампе, включ(!Ннойвфззу С, -век-И тором Осо: Так как £/воГ>1со, то лампа в фазе В будет ropeti-B более ярко, чем лампа в фазе С. Следовательно, ест фазу трехфаэ- ной системы э. д. с, к которой подключен конденсатор, принять заЩ фазу А. то фаза, к которой окажется подключенной ярко горящаяЪ дампа, есть фаза В. а фаза с тускло горящей лампой -фаза С. 1

Одним нз важнейших свойств многофазных и, в частности, трех-И фажых токов является их способность создавать круговое вращаюН песя магнитное поле.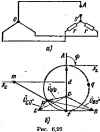

§ 6.17. Магнитное поле катушки с i

* током. Маг-

нитное поле одной катушки, по которой протекает синусоидальный ток. представляет собой пульсирующее (ие вращающееся) магнитное ноле. На рис. 6.24 изображена катушка, по которой проходит сину-соццальный ток i = / sinfi>(. Магнитное поле характеризуется вектх)-

* Под , которого яэь

1УЮЩ.ш полем понимают поле, вектор магнатной индукции я (пульсирует) вдоль оси сгадающей его катушки с током.

пм магшггаой индукции В. Направление В определяется направлением намотки катушки и направлением тока в ней в данный момент воемени Пусть буква Я означает начало, а К-конец атушки. Если ток входит в зажим Я и выходит из зажима К (это направление тока будем считать положительным: ему соответствует интервал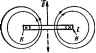

времени от О до л), то вектор магнитной индукции направлен вверх по осевой линии натушки. В следующий полуперпод, когда ток отри-идтелен, вектор В направлен вниз (пунктир на рис. 6.24), Таким образом, геометрическим местом концов вектора В является ось катушки.

§ 6.18, Получение кругового

цегося магнитного поля.

Круговое вращакще&я магнитное поле представляет собой магнитное поле, вектор результирующей магнитной индукции которого по величине неизменен и вращается с постоянной угловой скоростью а.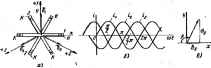

Рис, 6.25

Расположим три одинаковые катушки так, чтобы их оси были смещены на 120° по отношению друг к другу (рис. 6.25, а). Присоединим катушки к симметричной тре}4взной системе э. д. с. Пусть токи входят в начала катушек Я и изменяются следующим образом: i,-/ sinfi>(; 2=/ sin(<o(- 120°); (a = / sin(W-b 20).

Графики токов изображены на рис. 6.25, 6. Каждый из тсжов создает пульсирующее поле, направленное вдоль оси своей катушки.