тра Z. В ft-фильтрах существенно изменяется в зависимости о* частоты ш, находящейся в полосе прозрачности. Это обстоятелыпъо вызывает потребность изменять сопропшленне нагрузки в функции ci< частоты (особенно при приближения к границе полосы прозрачности) что нежелательно. В т-фильтрах при опредеяашых значениях коэффициента т, сопротивление мало изменяется от частоты (в пределах полосы прозрачности) и потому нагрузка практически ыожет быть одна и та же по величине для различных значении to. находящихся в этих пределах.

Качество филыгра тем выше, чем более резко выражены его фильтрующие Свойсгеа, т. е, чем более резко возрастает затухание в полосе затухания.

Фильтрующие Свойства четырехполюсников физически обусловлены возникновением в них резонансных режимов-резонансов токов или резонансов напряжений.

§ 5.2, Основы теории J-фильтров. Из § 4.10 известно, что если нагрузка Z (югласована с характеристическим сопрогнвлением Z четырехполюсника, то напряжение и ток в нагрузке Д гаяза с напряжением (j и током 1 на входе чет1фехполюсиика следующими соотнсяиеииями:

s=t7ie- h=h* где £=1п(Л-Ц=а-Ь/Ь.

Множитель е- определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения frona) на вхрде фильтра.

Если й=0. го e-°=ff=l н фильтр пропускает колебания затухания. Таким образом, в полосе прозрачности с = 0.

В полосе затухания о>0. Множитель е-, по модулю равный I, свидетельствдет о том, что напряжение и ток /я отстают соответственно от 1 и на угол Ь.

Фильтрующие свойства четырехполюсника рассмотрим путем сравнения выражения для коэффициента А четырехполюсника с равнк ему выражением пт)балического косинуса от аргумента a+jb: Л=Й1(а+/Ь).

Гиперболический косинус от суммы дп>К аргументов (с учетом того, что ch/b = cosb и sb/b=/sinu) можно представить следующим

ch(a-l-;fc)=chocosb-l-/shasin Ь. Для любого фильтра, собранного по Т-схеме (см. § 4.5), Л = 1 f + (Z,fZ,).

Для фильтра, собранного го П-схеме (см. § 4.5). A = i-i-(ZjZti. Из каких бы реактивных сопротивлений ни был собран фильтр, отношение Zi/Zj в Т-схеме и опюпкиие Z/Zj в П-схн всегда будл

действиташным (не мнимым и не компдассным) числом-отношение двух мнимых чисел всегда есть число действительное.

Следовательно, всегда будет действительным и коэффициент Д. Но если коэффициент Л действите.тен, то действительным должно быть и выражение равного ему сЬ(а-ь/Ь):

ch (о+/Ь) = ch о cos Ьу sh а sin Ь=Л,

Это выражение дейсшительно, еслн

shasinb=0, (5.1)

ТТри этом

chocosfc=Л. ib.2i

Уравнения (5.1) и (5.2) Используют для определения границ полосы .чозрачности и характера изменения угла b в зоне прозрачносги, а также характера изменения изэффициеита затухания а в полосе (полосах) затухания.

Равенство (5.1) для полосы прозрачности (d=0) удовлетворяется, так как sha = shO = 0. В силу того что chO=l, уравнение (5.2) для HOJKicu прозрачносги переход в слсзоющее:

со5Ь=Л. (5.3)

Круговой косинус (cos Ь) может изменяться в нредЕлак от +1 до - 1. Поэтому крайние значения коэффициента Л [являющегося функцией частоты - Л (to)] в полосе прозрачности равны ± 1, Полоса прозрачносги в общем случае лежит в диапазоне частот от до а-Значения ю, и to для фильтров НЧ и ВЧ (подробнее см, § 5.3) определяют путем решения уравнений

Л(и)==Ы. (5.4)

Д1Я псшосшых и заграждающих фильтров (см. § 5.3) н находят как корни уравнения Л(ео)=-1. Для них уравнение А (oj) - 1 дает возможность определить так называемую резонансную частоту Ид, находящуюся в интервале частот между и to.

Частоту, являющуюся граничной между полосой прозрачности и полосой затухания, называют частотой среза.

Характер изменения угла b в функции от для зоны прозрач-Hocni определяют в соогеетсгвип с уравнением (5.3) следующим оазом:

Ь = агссо8Л(со). (5.5)

Определим о и Ь для полосы затухания. В полосе затухания О >0. Уравнение (5.1) удовлетворяется при условии

т. е. при

и (или) при

sin = 0, Ь=0 , Ь = ±я,

(5.6)

(5.7)

(5.8) 131

Согласно уравнению (5.2), яри Ь=0 сЬа = Л(ш),

I при Ь±п

Aa = - A(fa).

Уравнения (5.9) и (5.10) позволяют по значениям А как функц Я €0 найти сЬо в полосе затухания, а по chc найти а и, таким образоц, построить кривую о-/(ы). Из уравнений (5.7) и (5.8) следует, в полосе затухания напряжение на выходе фильтра находите, либо в фазе (при Ь = 0), либо в противофазе (при Ь=-±п) с напря-i Жением Оу на входе фильтра.

В заключение необходимо отметить два важных положения.

1. С изменением частоты о меняются коэффициенты Б н С четы-i рехполюсника, поэтому изменяется и характеристическое ошротивле-ние Zc = y Б/С. Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная здесь теория фильтров), при изменении частоты нужно менять и сопротивление нагрузки.

2, В полосе прозрачности характеристическое сопротивлаше филь тра всегда активное, а в полосе затухания - чисто реактивное (ицдук-1 тивное или емкостное).

Если нагрузка фильтра ве чисто активная или ве согласшана с харвктеристк. ческим сопротивлением фялыра или если требуется учесть влияние вктивног сопротивления икпуктввных катушек на рабту фяльтра (что сушествснно juii , низких частот), то для построения зависимости t/i/(/j=/(<d) и зависимости угла (двига фаз между Ui и 0 в функции частоты можно воспользоваться, например, методом пропорциональных величин (см. § 1.12). Характеристическое сопротивление фильтра берут равным внутреннему сопрогналенню источника (генератора). При этом в генератор н фильтр работают в режиме

§ 5.3. К-фильтры НЧ и ВЧ, полосовые и загражлающие к-филъ-тры. Фильтрами ИЧ (ФИЧ) называют фильтры, пропускающие в нагрузку лишь низкие частоты: с (i)i=0 до щ. Полоса их затухания нахощпся в интервале от щ до со.

Схемы двух ФПЧ приведены на рис. 5.1, о, б. Характер изменения коэффициента затухания а и коэффициента фазы b качественно; иллюстрируют кривые рис. 5.1, е.

Под фильтрами ВЧ (ФВЧ) понимают фильтры, пропускаюшие в нагрузку лишь высокие частоты: с i до оо. Полоса затухания их находится в интервале от О до tOj.

Схемы двух ФВЧ приведены на рис. 5.2, а, 6. Характер изменения коэффициентов с и fc для них иллюстрируется кривыми рис. 5.2, в.

PaccMorpitM вопрос об изменении величины характеристического сопротивления в полосе прозрачности для Т-фнльтра НЧ (см.; рис. 5.1, а) и для Т-фильтра ВЧ (рис. 5 2, о), а также для Ш)Нль-Д тров. С этой целью в выражение Zc = VB/C подставим значения В и С в соответствии с формулами (4.18) и проанализируем получен-1 ные выражения.

Для Т-фильтра НЧ (см. рис 5.1, й)

Прн co=(j>j=0 Zc=T2t/C. С увеличением частоты уменьшайся, сначала мало отличаясь от значения УЖ/С. Прн достижении значения ю=Шг-)ЖС Z,=0.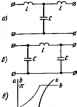

Рю. 5.1,

Для П-фильтра НЧ (см. ряс. 5.1, 6> Лля Т-фильтра ВЧ (рис. 6.2, а)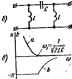

Р с. 5.2

ватом случае характер имевамя Z. отличен от характера изменения Z, для т-фильтра НЧ, а именно:

Z, 0 при a, B,= l 2tC. С увеличением ) (отрогавлоше Z. увеличивается и при о(-*-оо Z - VZUC.

Для П4ильтра ВЧ (рис. 52, 6)

Если фильтр предназначен для работы на частотах, находящихся BHSH г,осы1.роачности данного Ф-П JSZZiTr отстоящих от значения с, при котором г,-О, то сопршявлаяе наг-

рузки 2n на выходе фильтров НЧ выбирают равным шюроё соответствует ь> = щ = 0. Для Т-фильтра НЧ (см, рнс, 5.1, а) = V2L/C.

Для фильтров ВЧ обычно нагрузку соглаажывают со эиаченнем при ы->-оо. Для Т-фильтра ВЧ (рис. 5.2, а) ZYLJC. В но-

лосе (полосах) затухания Z оказывается чисто реактивным для Bcej

типов Ач})ИЛЬТрОВ.

Для того чтобы выяснить, индуктивный НЛН емкостный характд)

имеет Zc в полосе затухания, следует определить характер входного

сопротивления этого фильтра

(фильтр всегда работает в режше

согласованной нагрузки) для предельного режима, а именно: для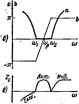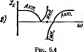

фильтров НЧ (рис. 5.1, й, б) при очень высокой частоте, а для фильтров ВЧ (laic. 5.2, о, б) при очень низкой частоте (теоретически при w-0), считая выходные зажимы сим закороченными. Тот же результат будет получен, если считать х разомкнутыми. В результате определим, что в зоне затухания Z имеет индуктивный характер для Т-фильтра НЧ (см. рис. 5.1, а) и П-фильтра ВЧ Шс Ь2, Б] К емкостный характер для П-фильтра НЧ (см. рнс. 5.1. 6} и Т-фильтра ВЧ- (рис, 5.2, а).

Полосоше фильтры представляют собой фильтры, пропуасающие в нагрузку лишь узкую полосу частот от Wi до лх. Слева от %

и справа от сл, находятся полосы затухания. Схема простейшего полосового ft-фильтра изображена на рис. 5.3, о. Параметры схемы должны удовлетворять условию LjCjLaCa.

Характ изменения а и Ь для полосового фильтра иллюстрируют к{давые рис. 5.3, б.

Без вывода дадим формулы дли определения параметров полосового фильтра ряс. 5.3, а по заданным частотам /i и и сопротивле-йию нагрузки фильтра при резонансной частоте /p = (i)p/2n: i; и-УЫ.: % 23) А = ; 4) 5) L,

Под загршкаклщиш фильтрами (рис. 5.4, понимают фильтры, в которых полоса прозрачности как бы разрезана на две части полосой затухания (рис. 5.4, б). Слева от ю, и справа от находятся две части полосы прозрачности.

В схеме простейшего заграждающая фильтра на рис, 5.4, а

Обозначим Vi=\lVl-yCi я kLi]! и эапЕшеи формулы для определения их 2 и фильтров рис. 5.3, а я 5.4, а. Для рис. 5.3. а

вля рис. 5.4, а

Для фильтра рис. 5.3. о в областа частот от О до Z имеет емкостаый

Для 4жльтра рис. 5.4, а

Рис. 5.5

характер, а в облает частот от до со-индук

в областн. частот от их Ло Юр Zc имеет индуктивный характер, а в области от Мр до Ша-емкостный.

Характер изменения 2, иллюстрируется крявымв рнс- 5.3, е и 5.4, е.

Пример 57.Всхеме рис. 5.1,а L = 10 мГ; С = 10 мкФ. Определить границы полосы прозрачности, закон изменения коэффициента Ь в полосе прозрачности, а также закон изменения коэффициента а в полосе затухания, построить векторэую диаграмму при © = = 2000 рад/с и 4=0,2 А.

Решение. Для Т<хемы

А = 1 -J-Zj/Za = 1 + }v>lj4>C = I - €o LC.

При A = \ u)i = 0. ПриЛ = -1 имеем -1 = 1-ttLC; отсюда b> = V2lLC=Ulb рад/с.

В полосе прозрачиосгн *=arccos >l=arccos(I-to Z,Q,

При частоте со = 2000 рад/с, находящЕяся в полосе прозрачности, ZcY{2L/C) - ft)L*=40 Ом. При нагрузке фильтра на характеристическое сопротивление напряжение на выходе 6j=-7a2t = 0;2.40=8 В,