Регулярное соединение тех же чещрехполюсииков оокаэаю w4 рнс, 4.6, б-перекрещены обе пч)ы концов второго четьх1юлкк> ника (при перекрещивании обеих пар концов все элементы любс матрицы остаются неизменными).

§ 4.9. Характеристические сопротивления четырехполюсников.

В случае несимметричного чешрехполюсшша (A=D) говорят о двух характеристических сопротивлениях Z, н 2, где Z-входное соп-

ротивление со стороны зажимов тп, когда нагрузка подключена к зажимам рд и равна 2 (рис. 4.7, о);

(4.24)

2(3 -входное сопрсгшвленне со стороны зажимов Р9, когда нагрузка Z псдалючена к зажимам пи (рнс. 4.7, б); при эгом коэффициенты А. и D шншлся местами:

2 DtiiBi DZrf+B

(4.25)

Совместно решая (4.24) н (4.25), найдем:

ZVAB/CD: Z,=VDB/CA. (4.26)

Учитывая, что А/С= Zt B/D -= Z. В/А = Z, D/C = Z. получим 2 = ад;; ZVZ. (4.27)

Если четырехполюсник симметричен (Л = £)), то 2=2,3=2, = V В/С, где Zc равно входному сопротивлению чешрехполюснина, когда он нагружен на 2 фис. 4.7, в),

§ 4.10. Постоянная передачи и единицы измерения затухашя.

Для симметричного четырехполюсника, нагруженного на Zt,

(7. = Л(;. + В/,£7,(Л+ВС); /,= /ЛЛ+1/ВС). Ксмиексиое число Л-Ц/Ж полагают равньм е*, где = 0 + p>=\n{A-\rY -постоянная передачи. Из формулы

0 = 0 и ti=i/je

следует, что модуль О, в е= раз больше модуля О, а модуль /, в е раз бо1ьше модуля По фазе С/ опережает О, на угол Ь, ток /ж Мерекает /j также на угол Ь.

Величина а хиктеризует затухание четырехполюсника. Единицами измерения затухания являются неперы (Нп) и беды (Б). Неперы определены на оаюве натуральных логари(1мов, а белы -на основе десятичных. Затухание в неперах

Если UifUg~e, то затухание равно 1 Нп. Затухание в белах ОБ - Ig I Si/S, 1 = Ig I t/,/t/, 1* - 2 Ig 1 t/,/t/, 1. a в децибелах

Если Ul бачьше в 10 раз, то затухание равно 20 дБ, если U/Um, то fl = 40 дБ.

Выразим непе через белы. Если Si/S,j= 10, то f/i/(/a = V16. При этом аип =-2 In 10= 1.15; ob=felO=l. Таким образом, 1 Б = = 1,15 Нп, а 1 Нп = 0,868 В = В,68 дБ.

§ 4.11. Уравнення четырехполюсника, записанные через гиперболические функции. Для симметричного четырехполюсника Л-форму уравнений (4.1) и (4.2) записывает иногда через гиперболические функции от аргумента g. полагая ADcbg, BZshg, С = -shg/Z. При этом AD-BCchgshg=l и

/, = .+сМГ1 Убедимся в справедпивостн замены Л на cbg:

еА+УВС. е- = ; chgi(e+e-) = A

Форма [записи через* гиперболические фикции используется, например, в теории фильтров (см. гл. 5).

S4.I2. Конвертор шротивлеями. Есла у невэанмного четырехполюсника S-С=0 и он иигружен на аажннах рд на сопрошатение Zh, то входное сопро-

о стороны зажимов п

где *1=0/Л, т. е. четырехполюсник преобразует (конвертирует) сопротивление - шротнвленяе ZJkt. Коэффициент ki называют коэффициептом конвертирования. Если Л я D HiKEfr одинаковые знаки, то Zj, имеег тот же знак, что и Z

(конвертор полоиштельного сопрогименип). если разные, то знак Zr протавопо-ложен знаку Z (конвертор отрицательного сопротивления).

Если укоЕвазтора 1=1, та t,=D. /i=fti/ . В этой случае кон-

вертор называют идеадьшлм ктаергтрои с преобразованием тока (14Щ 1кизм1енн<ш иапряжеятО.

о ki=l/A. Oi=0lki. U=h- Так.

Если у конвертора D= .

ывают tideoAbHUM конвертором с преобразованием напряжения. У конвертора есть Н- и С-ыатрицы. но отсутствуют Z- и У-ыатрицы.

§ 4.13. Инвертор сопротивлении. Если у невзаимного четырехполюсника А = = D=0. то ZB=(B/C)i\/Z и четырехполюсник в этом случае называют jweq

ного ссячхлнвлення). если знаки у В и С разные, то Zbi- Щв (инвертор i р8ца1ельного ашрогивленин),

У идеального инвертора входное сопротивление не зависит от того, к как шмам (рд или тп) подкяочена нагрузка.

У инвертора есть Y- в г-ыатрицы. но отсутствуют Н- и С-матрицы.

§ 4.14. Гнратор. Гиратором называют инвертор отрицательного сшротивле* и, шсюищй слЕточощую У-ыатрицу:

е е-про имость гнратора. Для идеального гиратора С-веществйшое числ Для гнратора /i=Gt/a,/а=~ G6/,.

Гиратор не- поглощает знергию. Он преобразует напряжение в

Еслн на выходе гнратора вкл1

сопротивление Zh. то его входное сопротивление ~ \I(&Z.

Представим гиратор как тре; люсник на рис. 4.8, а (зажим 3 схеме общий для входной и выходной I цепей). Его У-матрмца остается

меняой. если, оставив гиратор вепс ; авжным, в направлении стрелки пор нумерацию его зажимов. Гиратор является вевзгиыныи (необратимым) четырехполюсником, так как дли иегоУигУи- Практически осуществить гиратор можно, например, по схеме рис. 4.8. б, в-которой использоза-ны два управляемых напряжением источника тока: Gd и СО.

понимать линейный j

В четырехполюсник. Под а

содержащий транзисторов и sj

вающие связь между его входными и выходными величинами, щения.

содержащий пстЬшнкн энергии, но не JX ламп Рассмотрим

Рнс. 4J9

Положим, что в первой ветви тп актинного четырехполюсника рис. 4,9, есть источник а. д. с. во второй ветви pq-нагрузка Zu, а в остальных ветвях (3-р), находящихся авутрн четырехполюсника, имеются или могут иметься источники 9. д. с. индекс к может лрннимать значения ся 3 до р). Тогда,

= рнив по теореме котйпснеашш сопротивление Zg im:. 4.9, б), запишец выражения для токов /, н Ig.

,. д. с. t.

Осуществим короткое замы этом по вервой ветви протекает

(4.30)

[а зажинах тп к pq. При , а во второй-ток igkb =*

В (4.29) вместо J] EtVik подставим tkb а в (4.30) f вместо Oltb-Кроме того, заменнм*! на (/т.н 4 ва (7g. В результате получим:

г уравненнй (а) и (б) только тем, гно li-htik и la-kbk вместо tj и /а. , получающиеся ва (а) в (б) в результате

Уравнеияя (4.31) и (4.32) отличаются с что в их левых частях находятся соответственно /, Отсюда следует, что все уравнения, получают их преобразований, справедливы в для активного четырехполюсника, только в них /i следует заменить на li-lnk. а /g-на/*-/аи- .

Так. Л-Форме уравнений для пассивясжч) четырехполюсника iUt=AUz+Bls, it=CUs+Dls) соответствует Л-форма уравнений для активного четырехполюс-

[f?j= Аб+В (/е-/ям);

Ксвффншенты А. В. С, D активного четырехполюсника удовлетворяют условию AD-BC=l в определяются так же, как и для пассивного.

На рнс. 4.10 изображена одна из возможных Т-схем замещения активного

четырехполюсника. Сопротивлении Z. Za и 2s €Я1репеляют . А, В, С, D так же, как в для пассивного четырехполюсника, а э. д. заход;1тпо зненинм тоов Ukb /йк и сопротивлениим из уравненнй, ленных для режима €иновременного короткого замыкания входа и выхода (показано пунктиром на рве. 4.10):

bb(Zi+z3)-W,=£a; -/*ftZs+/aftft(Zi+z3)=£4.

Исследование работы электрических цепей часто проводят графическими методами путем поироения круговых в линейных диаграмм. Перед тем как приступить к изучению круговых диаграмм, рассмотрим вопрос о построении дуги окружности по хорде и вписанному углу.

§ 4.16. Построение дуги окружности по хорде и вписанному углу,

курса геометрии известно, что вписанным углом называется угол, вершина которого находится на окружности, а стороны являются хордами.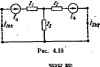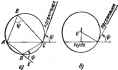

Рис. 4.11

Вписанный угол измеряется половиной дуги, на которую он опи-раегся. Так, Z АВС = (рис. 4.11, а) измеряется ADCf2, а Z ADG дугой АВС/2. Сумма Z ЛВС+/; ЛОС=я.

Угол EDC является дополнительным до я к ADC, поэтому LEDC-ii>.

Какое бы положение ни занимала точка D в интервале от А до С, угол между продолжением хорды AD (т. е. линией DE) и хордой DC остается неизменным и равным Ц\

Угол между продолжением хорды АС и касательной (полукасательной) к окружности в точке С также равняется углу

Центр окружности О на-ходатся на пересечении перпендикуляра к середине хорды и перпечд к1.чяра к касательной (рнс. 4.11, б). Из изложенного сл-ег, что если заданы хорда и вписанный угол ф, то для нахождения центра окружности необходимо: 1) восставить перпендикуляр к середине хорды; 2) под углом ф к продолжению хорды провести прямую, когарая будет являться касательной и окружносгн; 3) восставить перпевдикулкр к касательной; пересечение перпендикуляра к хорде и перпендикуляра к касателыюй даст центр окружности.

§ 4.17, Уравнение дуги окружности В векторной форме записи. Пос1роения. аналогичные оороенням рис. 4.11, о, р . .g

иогут быть выпшшшы и на шмплекс-

ной плоскости. В этом случае все хорды, например СА, DA, CD являются векторами.

На комплексной плоскости рис. 4.12 совместим хорду СЛ=Т с осью -I- 1. Если угол я1)>0, то от продолжения хорды его откладывают против часовой стрелки; если ijj<0, угол откладывают по часовой сфелке

Обозначим DA=G к С5=Й. Тогда

G+H=F. [ (4.31)

Вектор И опережает вектор б на угол % Пусть модуль вектора Я будет в ft раз больше модуля, вектора б. Тогда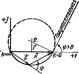

Если А=0. то и При fi=co E=F и С*=0. Под-

ставив (4.3П в (4.3IJ, получим

G(l+fte)=f.

1--Аб*

(4.31 -)

Уравнение (4.31 ) называют уравнением дуга окружности е векторной форме затгси.

При изменешш коэффициента ft от О до со меняются оба вектора G и Й. но так, что угол ifмежду ними остается неизменным, а сумма векторов равна вектору F, Конец вкюрад сжользит по дуге окружности, хордой которой является вектор F. Поэтому можно сказать, что дуга окружности является геометрическ[£М месгсал концов вектора С.

Рабочей частью Окружности, или рабочей дугой, является та часть окружности, которая по отношению к хорде лежит по обратную сторону от пмукасательной (рабочая дуга на рис. 4.12 вычерчена сплош-нсж линией, нерабочая - пунктиром).

Рабочая дуга меньше половины окружности при i]j<90° н ба1ьше половины окружности при if I > 90,

§ 4.18. Круговые диаграммы. Из § 3.4 известно, что синусоидально изменяющиеся функции времени (токи, напряжения) могут быть изображены векторами на комплексной плоскостн. Еслн процесс в электрической цепи описывается уравнением, по форме тождественным уравнению (4.3Г ). то геометрическим местш* концов вектора тока (напряжения), выполняющего в уравнении электрической цепи ту же роль, что и ви{Т0р с в уравн 1ин (4.3Г ), является окружность.

Под круговой диаграммой тока или напряжения понишют дугу окружности, являющуюсй геометрическим местсал конц(ш вектора тока (напряжении) при изменении по модулю какого-либо сопротивления электрической цепи и сохранении неизменными остальных сопротивлеинй, частоты и э. д. с. источников энергии.

С помощью круговых диаграмм производят графический анализ работы электрических цепей.

S 4.19. Круговая диатрамма тока для двух последовательно соединенных сопротнвлеяий. Пусть к источнику э. д. с. подключены последсватсльно ZiZje и Z==re/* (рнс. 4.13). Сопротавленне Z, неизменно, а Z может меняться лишь по модулю, так что угол остается постоянным. Ток в цепи

(4.32*)

где E/Z-=i~TOK в цепи прн короташ замьиаяии сопропшлення Z.