Комплексные входные -сопротивления нахрдят опытным путем с помощью ваттметра, амперметра и вольтметра по схеме, подобной схеме рис. 3.24, а, с тем отличием, что вместо двухполюсника за жимами тп или рц (в зависимости от определяемого входного сопротивления) подключают испытуемый четтлрехполюсник.

Определим комплексное входное сопротивление четырехполюсника при трех различных режимах его работы.

I. При питании со стороны зажимов тп и разомкнутой ветви pq (х. X. ветви pq. 1 = 0, ивдекс нуль)

2. При питании со стороны зажимов тп и коротком замыкании ветви pq (к. з., (/, = 0, ивдекс ft)

Zv. = Uiffik = Zifteift = B/D.

3. При питании со стороны зажимов pq и коротком замыкании зажимов тп ((/д=0)

Z = 2 = B/A.

Таким образом, для опредвленпя четырех неизвестных коэффн-циентов Л, Б, С, D располагаем четтрьмя уравнениями:

AD-BCl, Z=A/C. Z = B/D, Z, = B/A.

Составим разность

Имеем Умножим, (м) на (а): Отсюда

Zt/Zk-D/A.

ад =т -

(м) (н)

(4.15)

.Формула (4.15) позволяет через Z , Z п Zj* определить кОэ*- фициент А: после этого коэффициент С находят из (и>, В-нз (л> н С -нз /к).

Коэффициенты А к D имеют нулевую размерность, коэффициент В имеет размерность Ом. коэффициент С-См.

.Р - 1и было uafweHo. что Z, =7.815e-4°12- Ом; Z,. = .

= 12.5е Ом; Z,i=3.33e °33- Определять иаффшщекга А. В. С. D че- .

. Нахолкм

По формуле (4.1 подсчитаем:

/7.815e-/°M2.i?,.

C=>?/Z,o=1.28e*3S° 77.815e-/ °=0.166efS CM;

Пример 50. К зажимам рд (см. соЕДнкена нагрузка Zj=6-b/6 Ом; и /,. если /s= I А.

Решенве. По фориуда (4.1),

[В-ИСГОЧ1ШК э. д. с. Найтн i

. рис. 4.1) четырехполюгникя примера 49тая-Ui=AU+BU=U{AZ,+B)=

= 1 .(1.28е?39°40-.б1Л2е +4.26еП=14.85е 3** В. По формуле (4.2),

;i=C(/E+D/s=/a(CZ,+D) = 1.165e !3 д.

§ 4.5. Т- и П-схйяы замещения пассивного четы

1нка. Функции пассивного взаишсях) чепехпсыпосника как передаточного звена между источником питания и нагрузкой могут выполнять Т-схема (схема звезды рнс. 4.4, й) или MtBHBaJWHTHafl ей П-схема (схема треугольника рис. 4.4, б).

X-щ л0-*-1-09

Предполагается, что частота м фиксирована, Три сопрогивлн!ия Т- или П-схемн подсчитывают с учетом того, что схема замещения должна обладать теми же ктаффнцнентамн А, В, С, Л, что и заменяемый ею четырехполюсник.

Задача эта однозначна, так как схема замещения содержит три элеммпа и четырехполюсник характеризуется тоже тремя параметрами (одаа связь между А, В, С, D задана уравнением AD - ВС= 1)*.

Выразим напряжение 0 и ток 1у Т-схемы (рис. 4.4, а) чд>ез на.1ряжение (\ и ток I-

j), = J?, + ;A+/A = !/,(l+) + /,(z, + Z,+f). (4.17)

У невзанмного чешреит-осника йаИ. поэтому для него схема з щения образопаня ие тремя, а четырьмя элеметтами (см., например, схему з Щения транзистора в § 15.35).

Сопоставим (4.16) с (41) и (417) с (42). При conocTaRKunfl

пайлем:

Л 1+(ад): В=2,+2,+2А/2й C=tlZ D=1+ZJZ (4.11 СкдоватБльно,

г,- 1/С:

2, = (И-1уС; (4.11

A = (D-1)/C.

Формулы (4.1В) и (4.19) позволяют найти сопропшлення Z,. п 2э (рнс, 4.4, а) по коэффшшеитам четырехполюсника Л, С, Л. Ана

логичные выкладки для П-схемы (ркс. 4,4, б) дают:

2,=В;

Z5=B/(D-i):

2.=В/(Л-!).

(4,20), (4,21) (422) (4.23),

Есл ! четырсгаюлюсннк симметричный, то A=D п в Т-схеме мешения Zi = 2e, а в П-схеме Z6=Ze.

§ 4.6. Определение коэффициентов Y-, Z-, G-, В-форм записц уравнший четырехполюсника. Коинлека1ые коэффициенты Уц,

= В уравнениях (4.3) и (4.4) можно нанп! следующим

офазом:

*и = № при f/, = 0; У1, = /1/(УаИриг7, = 0;Уи-=/а/г7вПри(/. = 0.

Коэфищнешъ1 Zu, Z, - Zji, в уравнениях (4.5) и (4.6) определим так:

Zn = Oi}h при /j-O; Zi = Vjii при / = 0; Zs, = Oji npi /, = 0.

Аналогичным образом найдш коэффициенты и других форм записи, например Я-формы:

tivi. = Ojh при £/ = 0; И = }и при /i-O; Hs = ti при t/,=0. Обратим внимание на то. что У,2=Уи. Z,o = 22i, но Wj2=-Я, Gia = -Gai, а Вц, не равно Д даже по модулю.

Пример 51. Вывесга формулы Z-параыетрое для Тсхемы замещения четырехполюсника (рис, 4.4. di. Решение.

§ 4.7. Оиределе н коэффициентов одном формы уравиеянй через коэффициенты другой формы. На практике возникает потребность в переходе от одной формы записи уравнений к дфугой.

. ттдя TOit) чтобы коэффициенты одной формы записи каити через <ЛЬяцяеши другой формы, необходимо выразить какие-либо две ..шяковые ве-тнчины в этих двух формах и солоставнть нх, учтя Направления тхжов h и для этих форм. Так, для Люрмы ,

для Z-формы

(О) (п)

(> = .г +.г, (р)

(/,=/,z +;,z. (с)

Сопоставляя правые части (о) и (р) и учитывая, что тсж в вы-pajHCHiHi (р) равен току - в выражении (о), наточим;

Из (п) и (с)

Z =l/C, Z=DlC. При переходе от коэффиииентов Л-фсиы к коэффициентам других форм получаем:

К -0/В. К =у = -/В, У = Л/В;

Bji = A Bia = 6. Вя,=С. ВгаЛ.

Пример 5г. Определить У-параметры четареяпалюеника через Решение. Решим уравнения (4. и (4.6) относительно 7 получешше уравнения с уравяеняями (4.3) н (4.4). Получим:

Для Техемы (рис. 4.4. а)

.i=.(Z,+2/u,. y =(Zi+Z/u,. y =-ZU

В табл. 4.1 лани <

для перехода от одной формы уравиенвй четырехполюсников).

К любой другой (Л-ф*ч)ма-для

§ 4.В. Применение различных записи уравнений чегьфехполос-ника. Соединения чеггырехпопюсников. Условия регулярное . Ту

или иную форму записи уравнений примеияня, исходя из соображении удобства. Так, в теории синтеза цепей (см. § 10.510.8) используют обычно У--или Z-форму записи. Параметры транзисторов для малых перемшиых составляющих (см. § 15.35) дают в У-, Я- или 2-форм так как в этих формах нх удобнее определить практически.

При нахождении связи между входными и выходными велнчинамп различным образом соедгаенных четырехполюсников (при овредёле-

коэффициентов эквивалептаого четырекполюетика) иаюльзуюг 2-, G и Л-формы.

При последсшательном соединении четьфехполюспиков а а о (рис. 4.5, о) применяют Z-форму, при параллельном соеднпенян (рис. 4.5, б)-К-форму, при последоьательно-параллельном (рнс. 4.5, в)-Я-<1юрму, при параллельно-последовательном (рис. 4.5,г)- С-форму, при каскадном {рис. 4.5, aj -Л-форму.

Форму записи уравнений выбирают исходя нз -удобства получнЯ матрицы ахггшното четырехполюсника. Так Z-матрипа псслеповательио-; соединенных четырехполюсников равна сумме Z-матриц этих четыре- <, полюсников, так как напряжение на входе (выходе) з*свнвалекшогО( четырехполюсника равно сумме напряжений на входе (выходе) составляющих его четьфсхполюсишздв. У-ыатр1ща параллельно соедайенных четырехполюсников равна сумме их V-матриц. Аналогично и в отно-

шении Я-матрнцы при последовательно-параллельном н С-матрицы нрк параллельно-последсжательнсм соединениях тьфехполюснитов. При каскадном соединении трк и напряжение на выходе первого четырехполюсника равны входным току и напряжению второго четы-

рехполюскика, поэтому Л-матрипа двух каскадно соединенных четырехполюсников а и Ь равна произведению Л-матр1Щ этих четырехполюсников:

ВЛ\А В,

СаАь+Djo ад+ад

при параллельном, гос;адовагельном, параллельно-последовагель-ном п последовательно-параллельном ооедшениях необходамо соблюдать условие регулярности соединения четырехполюснирюв-чер оба пертнчных зажима каищого чепфехполюсиика должны течь равные по величине и противоположные по направлению токи; то же и по отношению к вторичным зажимам каждого четырехполюсника.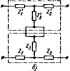

При рлпрном соеднншии йитрица каждого четырехполккяика должна оставаться такой же, .какот[ она была до соединения четырехполюснике .

\/Г1ример нарушения условия регулярности при госледователыюм одкнении показан на рис. 4.6, а Так соединять четырехполюсники 1 п 2 нельзя, поскольку сотротивления п Z второго четырехполюсника оказываются соединенными параллельно, что приводит к изменению 2-матрнцы второго четырехполюсника по сравнению с Z- атрнией уЕ;1(ипенпого второго четырехпсиюснпка.