где ft-нешгорое пропотолыюе число, Оы\ то

=+77+ f>= H+Tic(3-66)

С учетам равенства (3.66) перепишем уравнение (3.62) следующим образом;

Фа(? + М + 7) = А/ - (3.67)

Из сопоставления уравнений (3,63) и (3.67) следует, что, если ток /в источника тока в схеме рис. 3.44, б изменяется с той же угловой частотой, что и э. д. с. £ в схеме рис. 3.44. а и численно равен а параметры обеих схем согласованы в соответствии с уравнением (3.№), то при ft = 1 Ом закон изменения во времени гютенцнала фо в схеме рис. 3.44, б совпадает с законом изменения во времени тока / в схеме рис. 3.44, я.

Если свойства какой-либо из схем изучены, то они полностью шгут быть перенесены на дуальную ей схему.

Между входным сопровлением Z c, исходного двухполюсника и входной проводимостью Уду,л дуального ему двухполюсника существует соотношение Z = feyj,sj,.

Из формулы (3.66) получаем соотношение между частотной характеристикой чисто реактив1юго исходного даухполюсника Х (ы) и частгаоб характеристикой дуального ему тоже чисто реактивного двухполюсника Ьад., (ь>). Действительно, так как =(ы), а Уд - ~itsy,Af). то Х ,(ш)= -fti),j, (e.), т.е. частотная характеристика дуального двухполюсника получается из частотной характеристики исходного путем опрокидывания ее относительно оси ы и деления на масштабный множитель ft.

Каждому элйленту исходной схемы (схемы с источниками э. д. с. Е и параметрами R, L, С) отвечает свой элемент эквивалентной дуальной схемы (схемы с источниками тока /, н параметрами g С, L).

§ 3.44. Преобразование исходной схемы в дуальную. Каждому незавпсэяаому контуру исходной схемы, а также области, являющейся вненшей по отношению к схеме, соответствует свой узел дуальной схемы-

Если в какой-либо ветаи исходной схемы, являющейся смежной между двумя контурами, имеется п последоеатепьно включенных элементов, то этой ветаи соответствует п параллельных ветвей, соединяю-щнх узлы дуальной схемы, которые отвечают этим контурам.

Так, источнику э.д.с. Е исходаой схемы рис. 3.4а отвечает в дуальной схеме источник тока I, (pic. 3.46, 6). а источнику тока /в - источник э. д. с. Е; активному сопротивлению R - проводимость g,; индуктивности емкость С,; емкости С -индуктавносгь Для ореобразовання исходной схемы в дуальную поступают следукяцнм образом. Внутри каждою независимого контура (и во внешней области) ставят точки и называют их. Эта точки являются узлами эквивалентной дуальной схемы.

В схеме рис. 3.46, а три независимых контура, поэтому внутри них ставим точки /, 2, 3 (точка / соответствует первол кштуру, ,ечка 2-второму, точка 3 -третьему).

Во внешней по отношению к схеме области ставим точку 4. Между полученными четырьмя узлами проводим пунктирные линии-ветви дуальной схемы. Sfra линии проводим через элементы неходки схемы {R, L, С, £ ) и в дуальной схеме рис. 3.46, б включаем в них соответствующие эквиваленты.

Узел 1 на схеме рис. 3.46, а соединен с узлом 4 одной пунктирной линией, так как в ветви, являющейся смежной между первым контуром и внийней областью, включено лишь одно сопрогавленпе (активное сопрогивлиш Ях). На схеме рис. 3.46, б между узлом / и узлш 4 включен активная пр(шодимость gRiIh.

Узлы J и 2 на схеме рис. 3.46, соединены двумя пунктирными линиями (одна из них пюходат через источник э. д. с Еь, другая-через индуктивность 1Д поскольку в ветви. Рис. 3.45 являющейся смежной между

ко!пурамн 1 W 2, последовательно соединены два апемеша схемы (Eg и Lg). Узлы / н 2 на схеме рис. 3.46,.б соединены двумя ветвями. В одну из них включе!! источник тока Дв, в другую -емкость CpsLs/ft (элементы, дуальные Ёь и -а).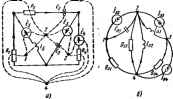

Рис. 3.46

Положительные направления токов нсточгвков тока в д1уалы1Ык сяеме должны бшь согласованы с положителыялмв направленняда э. д. с. источников э. д. с. в нсходной схеме. Еслн прт обходе жжтура по часадой cipejote какан-то э. д. с этого контра совпадает с напра-

вяеняем обхода контура, то ток знивалентного ей источника тока должен быть направлен к ft-уму. Если ток по некоторой ветви исходной схемы совпадает по ваправлеиию с папраалением обхода ft-контура тон дуальной схеме стрелку на соогаетслующей ветви направля1от ДУ ь в ВВДУ при составлении vi нзанмко дуальных схем (см. § Б 3)

Исхвдную н дуальную ей схемы называют ешимт обратными.

j,m, >Ttjrr характеризуем сяяусотоально язменяющаяс

ГГ , . ук1зьш.юп1ей положительное нтравленае для

=теяТе,ж -,Г.,г; =-я bssr кгг -=.:.т г %;г.еГ =.г=~

Sri . РЩгаРочь f. О. S. 8. Записать уЕлте pesoiLt

.SSSrr Т ; Г ?, Р м е ряс. 3.26.. npi з неяин Л я неиаяевиих £. R. (., и. Чю Поиямакп под дойротиостио 1щду]Ш1вноб катуошн конденсатора и резонансного контура Q? 9. Как по ввду часютией характеристики X (ш) реактивного двухполюсника можно оппепр

ZlSSJ!;f T K Т 5 е резонансные при гамененни <а? lO. Какой должна быть взята нагрулка, пвисоединяемая к яктик онХГ - ь аксиальная 2цнос? 11. дГ

опредежнне согласующего и щдеалыето трансформатора 12 Как в пясчете v ttj катмн? Гка:

стадяют развязывание, магнитносвязанных цепей? 14. ОЬосмулиповатъ leobwiv о балансе активных и реактивных мощностей. 15. К.к ЭДГровэть дуГл изисходкой? I . Решите задачи 5.1. 5.5; б.? LttllfS, 55;

чепкхполюсник и круговые диаграммы

§4.1. Определение четырехполюсиюса. Четырехполюспи-

Иоы называют электрическую схему, имеющую два входных и два выходных зажима. Трансформатор, линию передачи энергии, мостовую схему и т. п. можно рассматривать как четырехполюсники.

Принято изображать четырехпсшюсник в пид прям(гольника с выходяшдми из него концами (полюсами) тп и pq (рис. 4.1, с). Если четырехполюсник содержит источники электр1 ской энергии, то в iTpflMoyit ibHHKC ставят букву А (активный); если буква А отсутствует, то это значит, то четьфехполюсник пассивный.

Входной ток обозначают входаое 11апряжеш1е Uu токннапр жение на выходе /, и f/,.

Чешрехполюсник является передаточным звеном между источником питания и нагрузкой. К входным зажимам тп, как правило, присоединяют источник питания, к выходным зажимам рд-нагрузку.

Предполагается, что нагрузка чегаремюлюсника п напряжение па входе пра работе четырехполюсника в качестве связующего звена

nrvT изменяться, но схема внутренних соединений четырехполюсника и значения сопрогпфлепий в ней остаются неизменными.

6 4 2 Шесть форм ваписи уравнений четырехполюсника. Четы-гхполюсник характеризуется двумя напряжениями Ui и ч Двумя 5ками /, п /а- Любые две величины ш четырех можно опредеппь

/? р т h

через остальные. Так как число сочетаний нз 4 по 2 равно 6, то возАюжны следующие 6 форм записи уравнений пассивного четырехполюсника;

Лф>рма: Lli = AO,+Bl (4.1)

;. = /,+D/,: (4.2)

У-форма: li=TulJi+Y,jyi (4.3)

. = Уа(/,-ЬУ,Л; - (4.4)

24орма: U-ZJ,+Zj (4.В)

U,-ZJ,+ZJ,: (4.6)

.форма: IJ, = HJ,+HM . (4.7)

0-форма: А = Рц(/,-Ье /,; . (4Л

В-ш: и,В и,+В 1,; (4.II)

,-B (>,-fB ;,. (4.1?)

Обратим внимание на попарную инверсию Y- и Z-орм, А- п В-форм, Я- и С-форм.

Исторически сложилось тан, что для vl-формы (ее будем считать основной) положителы!ые направления для токов и напряжений соответствуют рнс. 4.1, а; дляУ., 2-, С-форм -pic 4.1, б, В-форые- рис. 4.1. е.

Обралш внимание на то, что ток на рис. 4.1, блаправлен противоположно направлению тока на рис. 4.1, о.

На рис. 4.1, в ТОЮ! /, и /j изменили направление по сравненшо с токами /i и иа рнс. 4.1, а.

Рассмотроше уравнений начнем с Л-формы.

§ 4.3. Вывод уравнений к Д-форме. Комплексные коэффициенты А, В. С. D в уравнениях (4.1) и (4.2) зависят от схемы внутренних

соедннепнй четцрехполюсн1Тка, знашнЁ сопротивлеинй qceMbi и частоты. Для каадого четырехполюсника лх можно определить расчетным али, опытным путем. Для четырехпояюсшщов, удовлетворяющих условию взаимности, коэффициенты связаны соотношением

AD~BC=l. (4.т

уравнения-(4.1) и4.. С этой целью к важнмам ии

подключим источник э. д. с. Ё грузку Z, (рис. 4.2, а).

i, а к зажимам pq - кй-

ir>- я *- V

OJ 6)

Рис. 4.2

Напряжение на нагрузке UJZOpj. Согласно теореме ком- цёнсадви (см. § 1.17). замшим нагрузку Zj 1кггочником э. д. с. с э. д. с. Et=U и направленной встречно току /а (рис. 4.2,6). Запишем вы- рэжения для токов 7, и /я. выразна их через э. д. с. ti, Ё и входные II взаимные проводимости ветвей у, у;

/i-iyii-sffu; (а)

Л-£1!/.1-.г. (б)

Если токи li и /g рассматривать как кштурные токн, то э. д. с. контуров, совпадающие с направлением контурных токов, войдут в уравнения, подобные уравнению (1.7), со знаком плюс, а э. д. с, не совпадающие с направлением соответствующих контурных токов, --со знаком шптус.

В. д. с. £ i направлена согласно с /i, поэтому она вошла в уравнения (а) н (б) со знаком плюс; . Д. с. Ё направлена встречно поэтому она вошла в эти уравнения со знаком минус.

Для линейных четырехполюсников, ие содержащих нелинейных влементов (для взаимных четырехполюсников), согласно принципу взатшостн (см. § 1.16), Уц=Уи. Из (б) найдем

Подставив (в) в (а), получим

Обозначим:

А sJyn. В= \1уа, C = (yu!f-yjyi)fyu, D = y fy . () В уравнениях (в) и (г) замсЕнш на d и Ё а (7, и восполь-80В8Ш1ШСЬ обозначениями (д), получим уравнения s Л-форие:

и = Аи+В1\:

Проверим вшолаенне соотношения (4.13) для взаимного четырехполюсника:

ЛС-ВС= ~ 1,

Для иевзаимного четырехполюсника уФуи AD - BCyijIyU

Далее обсудим соотношения, котошле имеют место между 0 и и [/а и / если источник э. д. с. £, присоединен к зажимам pq, а нагрузка -к зажимам тп (рпс. 4.3).

Как п в предыдущем выводе, заменим нагрузку Zj на источник э, д. с. с э. д. с. £j, направленной встречно току н запишем выражения для токов fj и /в:

+ (С)

/i=-fife+Ai. (ж)

Из (е) наГщем Подставим (з) в (ж):

Заменив J?,-, иа и Ё на (7, и воспользовавшись обозначениями (д), перепишем две последние строчки сле-дуюиуш образом:

C\D0+BU (4.14)

Ii = CUi+At. (4.14)

Таким образом, уравнения (4.1) и (4.2) характершуют работу четырехло- Рас, 43

люсника при питан1П1 со сторотя зажимов тп и присоедниенни нагрузки к зажимам рс/, а уравнения (4.14) и (4.14) -при его тгганви со сюроны авжимов-р и присоедннепии нагрузки к зажимам тп.

Чешрехпотосник назыпают симметричным, если прн перемене местами 1к:гочника пнтаиня н нагрузки токи в исгочнике питания и нафузке не изменяются. В снм.летричном четырехполюснике Л =£). Уравнения (4.1) н (4.2) иногда записывают так:

Ot-Ajy+AuUl (4.17

LAiO+Aj (4.2*)

= А: Ли = В; Ла=С; Л-Д

Л-формы записи ураввеинВ или А, В, С, Д входящие

гае Л =

§ 4.4. Опредемиве -коаффицие четырехп0Л>а!ика К0Ш1Л(1КсныеК--,. . . - -

в уравнения (4.1) и (4.2), можно определить по формулам (д). если схема внутренних соединений чегирехполюсника и ее параметры известны, либо используя входные сопротявжипя чегырехполюспика, полученные опытньы или расчетным путем.