закону Кирхгофа для согласного включения катушек:

Совместное решение их дает: /,= бе-- ** А; /2=Ч4,27ев** А.

Топографическая диаграмма, совмещенная с векторной диаграммой токов, изображена иа рис. 3.41, б.

Рассмотрим вопрос о трено-се мощности из одной ветви в другую вследствие магнитнШ связи. Если ветвь k с током и. ветвь q с током связаны магнитно и взаимная индуктивность между вегаями Л1, то магнитный 1ктж из ветви вветвь q переносит комплексную мощность, равную прсяжедеиню э. д. с. взаимоиндукции в q-ex-ви гр/соЛ(Д на сяпряжмнуй комплекс тока -ветви, т. е,

Знак минус соотвегсгвует согласному, плюс-встречному соединению.

Рнс. 3.41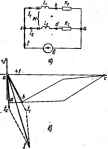

в параллельном, гослвджатель-

§ 3.40. Резонанс в кагннтиосвя-аанньк колебательных контурах. В

§3.23- 3.27 были описаны резонансные Явления t , ,

иоми последовательно-параллельном резонансных контурах. Рассиотрии резонанс Ь капцшюсвязшшых кС1.теботепьиых контурах-в схеме рис. 3.42, а, .часто применяемой-в радиотехкике. G целью упрсяцения выкладок положим L,=L,=£.; С,-с2=С; 1г],==ЙЕ=А, что дает возможность отиосительио легко выявить основ-ные зак оно мерности резонанса в этой схеме.

Составим уравнения по второму закону Кирхгофа:

/,= /

Напряжение а KoioicaTppe второго контура ... 1 М 1

Пусть OcJE=K,. Тогда . <-C-

R

ilT Oil Vi/C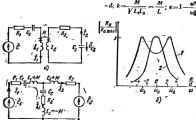

в свою очередь.

При малых отклонениях а от m , вы1*егя в iit4Ii( ibtcjib Bi.nowa / \ скобку i ,L. , спользо,., ук Г5оз Т1

. Модуль

при ft::>rf имеются три аксфемума; минимум прн е=0. т е ппн .

При имеется -----.

3 42. б). По оси абсцисс иа этом рисунке

один экстремум: максимум при £=0 (кривая 2 на e/d, по оси (фданат-

э (/g) контуров в функции от Bjd при А>й

.(С,/к. хИ МК. .- -

Токн первичного (/J и вторичт также имеют двугорбую форму.

§ 3.41. Л>азвяэываняев магнитносвязанных цепей. Иногда в литературе можно встретить расчетный прием, который называют развя2Шапием мапалтносвйзаниых uCTjrf (катушек). Суть его е том, что исходную схему с машитносвпаянными влдук-тиеяостями путем введения дополнительных индуктивностей и изменения имеепшкся преобразуют так, что магнитнен сввзь меада всеми ицпуктавногтями в лреобра-з(жанной cxewe отсутавует.

Так как преобразования осуществляют на основе составленных го законам Киргофа уравнени!! для исходной схемы, то вновь полученная и исходная сксиы в pai-четном смысле полностью эквиваленты.

Составим, например, схему, эквнваленшую схеме рис- 3.33. С этой целью в уривненни (в) (см. § З.Зб) заменим h а /i-/а н в уравнении (г) на /3+4. Заме!(у одних токов др>тнмн пршэвдднм так, чтобы в каждое из получающихся после замены уравнений входили только те токн. которые текут в ветвях рассматриваемого контура. В данном случае получим;

Урэвпениян (в) и (г) соответствует схема рис. 3.42, е. Сопоставляя схемы рис. 3.33 и а42.в. миечэсм. что Ц заменена на (ti+Af). L3-M (tj+Af). а во вторую ветвь введена отрипательная индуктивность L =-М (физически осутс-сгеить отрицательную индуктивность в цепи с линейными элементам нееознаялю).

§ 3.42. Теорема о балансе активных и релктнвимх монростей. В любой лнней-Еой электрической цепи сумма юсшвпых мощностей источниковэ. д. с. равна сумме активных мощностей приемников, а сумма реактивных мощностей источников 8,д. с-сумме реактивных мощностей приемников энергин.

При этом под реактивной мощностью прнемщ1ков энергии понимают сумму лроизвеннй квадратов токов ветаей, умноженных на реактивные сопротвления вегвей. подсчитанных без учета явления взанмоицдукцни, плюс алгейрйическая Сумма McfOHocTai, переносимых магнитными потоками нэ одних ветвеВ в друпм вследспир явления взанмоиндукцнн. Прв этом имеется в виду, что без учета взанмоиндукцнв оойсчнтываклся пклько реактивные сопрспнвлення ветвей, а юки - с учетом этого явления. Пусть схема содержит / узлои, в ветвей и все ветнн или часть нх связаны лруг с другом ыягиятао. По вервому закону Кирхгофа, сумигг

2; р=о или S/ p=o.

Умножим кащдое слагаемое той суммы на потенциал А-узла ф; Просуммируем аналогичные выражении для всех / узлов схемьц

X Ф* S v=t-ft=i p=i

в двоВную сумку любой ток схемы, нагфиверток / . входрг дважды и imim i с разными знвками. Действительно, лрн k=m и р=в слагаемое равно чи/ в а при k=g и р=т рав;:о ф,/ . Так как то эти слагаемые можвд

объединить и получить/и,(фУ-фд). °

Пусть какая-то еетаь схемы, например ветвь kg. магнитно связана с ветвью sr тек. что сопротивление взаимоиндукции между ними Xj (рнс 3.43). В соответсгаии с рнс 3.43 для ветая Qk

для ветвн sr

Если принять, чго Пд=1лъЯ. /. =/,У , В учесть, что hghg то умма двух слагаемых

Таким образом, попарное рассмотрение слагаемых дао&кй суммы позволяет переписать ее в вцде

i: v*p=i:-i/,+/2i: (3.60)

Слагаемые типа Ё представляют собой прошведеш э.д. с. находящейся вветвн kq (fe и р-т кущие индексы узлов схемы, иа сопряженный комплекс тока VttA же ветвв; квадрат кадулн тока ветви kp; ZpR+fX,

В сумму у25]/Усо8( Ф по одному разу входят попарные произведения токов магнитно связанных друг с другом ветвей, умноженные На светствющие сопропюлення иззямоянщцнн н вакосниусы углов между токаМй

Например, если в некоторой схеме магнитно связаны три ветви (ветви 12 13 в 25), то вторую сумму в (3.6( записывают как

Левая и правая части формцпы (3.60) представляют собой комплексы. Рабе -стао лействительных частей тжнлекож дает формулу

№i;v.p=SJ,v (3-И)

в равенство мнимых-формулу-

1ш %Х,+22 (3.62)

В формуле Х принято вааожилльным г

потоков взанмонндукцни и самоиндукция ветвей kg i встречном т иаправлевив. Формулы (3.61) и (3.62J

убедиться в справедливости тео-

. -,- . . : рис. 3.40.в.

е. Активная мощность, доставляемая i

Пример 48. По данным примера 46 в ремы о балансе мощности прнмешггельно * Решеине. Активная мощность, дос

Re£=ReIOO.I7,7e °=I770cofi63>=800 Вт. Активная мощность, гслребляемая прн ииккамн, / R = I4,12 -4=800Bt. Следо-вателыи , равенство активных моиностей действительно выполнено. Реактивная можнссть источника э.д.с. 1т£/= 1770яп63== 1582 ВАр. Реактивная мощность Ериеиников анергии с учетом согласного включения катушек n,aL,+/laL+2hlM cos = 17.7s 2-Ы4.6?. 3-1-2.17.7.14.6cos(63°-144)== 1582 ВАр. Таким образом, баланс реактивных мощностей также удовлетворяется.

§ 3.43. Определсиие дуальной цепи. Две электрические цепи пазьГ-

вакп- дуальными, если закон иэмепешя контурных токов в одной нз них подобен закону изменения узловых потенциалов в другой*. В качестве простейшего примера па рнс, 3.44 изображены две дуальные цепи.

Схема рис. 3.44, а .состоит из источника э. д.с. £ и по- f)

следовательно с ним включенных актввпого, ипдуктнвного Р**-и емкостного сопротивлений

{R, L, С). Схема рис. 3.44, б состоит нз, источника тока h и трех параллельных ветвей. Первая ветвь соджит активную проводимость gsi вторая-емкость С третья-индуктивность

Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для-схемы рис. 3.44, я уравнение яо методу контурных токок

(3.63) обоз-

/(i?+j tH-Jj-)=£.

а для схемы рис. 3.44.6-по методу узловых потенциалов* иачиБ потенциал точки а через ф.:

(3.64)

Если параметры схемы рис. 3.44, б (g L С,) согласовать с параметрами схемы рис. 3.44, а {R, L, С) таким образом, чю

Rlg, = L/C, = LjC=k, (3.65)

Здесь расшсярены вопросы дуалькосга для таких цепей, которые путем нзвгенення их начертания могут быть изображены на плоскости без взаимного пересечении ветвей (такие цепи называют пмиарншш).

Потенциал второго уэла схемы рис. 3-44, 6 принят равным нулю.