§ 3.38. 01феделепие взаимной индуктивности ошатным путещ

Обсудим два практическн важных способа сшытного определения взаимной ивдтсгивностя ЛГ двух магнитносвязанных катушек.

Первый способ. Годелаем два опыта, В первом из них включим, катушки последашельно й согласно. Измерим ток и напряжение на

JwL,h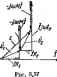

Рнс. 3.38

входе и активную мощность цепи. Во втором те же катушки включим последовательно и встречно и также измерим /, U, Р. По результатам иажреиий найдем:

X ..гл = . (1а++ 2Л0; Х., = w (L,+- 2Л1). Разность Хсвм -?Bcip = 4 >. следовательно.

(аббь

Второй способ. Подключим первую катушку к источнику синусоидальной э. д. с. через амперметр (рис. 3.38), а к зажимам второй катущки подключим вмьтметр с большим внутр€мшвд сопротивлением,! Измерим ток Ii и напряжение U.

Мпювенное значение напряжения Иа=Л1 Егодействукадее зна- . чение [/a=coAt/i. Следовательно,

M = i/,/ft)/i. (3.57)

. Пример 45. В схеме рис, 3.38 вольтметр показал 100 В, ампер- Г метр Ш А; iu = 314 (г*. Определить М.

Решение. По формуле (3.57), М= 100/(314-Ш) = 0,0319 Г.

§ 3.39. Тра1к:фо штор. Вносимое сопротавление. Трансформатор представляет собой статическое (т. е. не имеющее подвижных частей), устройство, служащее для преобразования переданного во временя напряжения по величине, а также для электрического разделения цепей*11 для преобразования озпротнвленнй по величине. Передача энергии из одной цепи в другую производится трансфокатором благодаря явлению взаимгашдукции.

Трансфсматор имеет две о&>ютки, наяоднеся на о&цем сердечнике. Магнитную проницаемость сердечника йудем полагать постоянной.

Параметры первичной обмотки Ri и L; вторичной - /?, и L. Взаим-ая индуктивность между обмотками М (рис. 3.39, о). Сопротивление Кагрузк подключенной к зажимам вторичной обмотки, равно Z. Ё

-&

ft, L,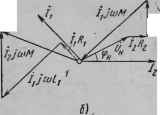

Рис. 3.39

Выберем положительные направления токов н /g. Обозначим

[напряжение на нагрузке 7 . Запишем уравнения в комплексной форме: для первичной цепи

/iRi + /i/(oLi + /J(oM = £i; (3.58)

для вторичной цепн

+/2/o)L3 + /i/o)M + L = 0. (3.59)

На рис. 3.39, б качественно построим векторную диаграмму, полагая, что нагрузка Z = z e имеет индуктивный характер. Ток 1 направим по оси + 1. Напряжение на нагрузке (J опережает ток/з на угол ф . Падение напряжения совпадает по фазе с током /3. Вектор /a/wLj опережает ток /2 на 90°.

В соответствии с уравнением (3.59) вектор JJaM проводим так, чтобы геометрическая сумма падений напряжений во вторичной цени равнялась нулю.

Вектор тока отстает от вектора IjaM на 90°. Вектор ijR совпадает с вектором тока по фазе, а вектор /i/foLi опережает на 90 .

Вектор IjaM опережает /2 на 90°. В соответствии с уравнением (3.58) геометрическая сумма /-f/i/mLi +/о/мМ дает Ё.

В (3.59) подставим f/ =/.zZ =/2 (?и +/Х ) и решим уравнения (3.58) и (3.59) относительно Ii.

(/?i+?bh)+/(Xi-X .,)

[Где и Х -вносимые из вторичного контура в первичный актнв-[Ное и реактивное сопротивления;

Хн =

j((uL2 + X ).

Вносимые сопротивления представляют собой такие сопротивления, которые следовало бы внести в первичную цепь (включить последо! вательно с к Х, чтобы учесть влияние нагрузки вторичной цепи трансформатора на ток в его первичной цепи.

Пример 46. Определить токи в схеме рис. 3.40, а п построить топографическую диаграмму, совместив ее с векторной диаграммой токов, полагая o)L. = 2 Ом; (uL, = 3 Ом; ч>М~\ Ом; R. = Ом-£=100 В.

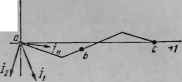Рис. 3.40

Решение. Составим уравнения по законам Кирхгофа. По первому закону Кирхгофа,

При составлении уравнений по второму закону Кирхгофа обход контуров будем совершать по часовой стрелке; тогда

/Jo3Li + /\,/a)AH-/ R = i-;

В двух последних уравнениях заменим / на - i, {R + /coLi) + /, (/COM - R,) = Ё; i, ij<oM - R ) + /, (R + /(oL,) = 0. Подставим числовые значения:

i,(i + 2j) + I.Jj-i)=l00; /i(/-4) + /o.(4 + 3y) = 0.

Решение уравнений дает: /i=17,7e- А; /2= 14,бе * А; / == = /\-/ =Г4.12е9=б* А.

На рис. 3.40, б изображены топографическая диаграмма и совмещенная с ней векторная диаграмма токов.

Пример 47. Построить топографическую диаграмму для схемы рис. 3.41, а, совместив ее с векторной диаграммой токов. Две ветви схемы связаны магнитно. Значения параметров: wL = 3 Ом; coL., = = 4 Ом, соМ = 3 Ом, = = 2 Ом, Ё= 100 В,

Решение. Обозначим токи в ветвях через и и ток в нераз-ветвлеьной части схемы -через /. Составим уравнения по второму