прямая / рис. 3.28, б выражает зависимость aLi=f (ш); кривая 2-а кость -j=/(fi). кривая 3-зависимость Х=/(и). Значение €в=ш при * ром кривая 5 рнс. 3.28. б пересекает ось абсцисе. представляет собой углоЬую частоту, гри которой в двухполюснике рис. 3.27, а наступает резонанс нйй№-жений.

При а<.щ входное сопротивление имеет емкосгаый характер (X отрицательно), при и>Мо-индуктнЕныП (X положительно). Так как для схёгш рнс. 3. 28, о реактивная проводимость fc=i;X. то кривая 6=/(и1 рис. 3.28. в взаимно обратна кривой 5 рнс. 3.28,6. При 6i<(Uo входная провоцимисть ииеег емкостный характер, при ю>Ши-ивду пивный. В точке ы=ш крнаая Ь=) претерпевает разрыв от -с до +с . Для двухполюсника рис. 3.28, г входная проводимость и входное сопротивление соответственно:

Завнси-чостн Х=/( в) я ft=/(<i* для схемы ряс. 3.28, г изображе! иа рис. 3.28. а, е. При ч>=(о1 реактивная проводшаость fe=0, а реактивное сопро-тивленяе претерпевает разрыв от +оо до -со. При и=(о; в двухполюснике рис 3.28, г имеет место резонанс токов. Таким образом, го виду характеристики А=/((о) или fc=/(ti)) можно судвть о тон, какого типа резонансные режимы в каком кмшчестае возникают в нсследуетюй схеме при изменении частоты от до оо. Точка, в которых X=/(w) пересекает ось абсцисс (кривая fe=/> претерпевает разрыв от -оо до +оо1, дают значения угловой частоты, при которых в исищдуеиой схеме возникают режимы резонанса напряжений.

Точки, в которых ризан Х=/(и) претерпевает разрыв от -[-оо до - {кривая *=/(и) пересекает ось абсциссЬ соответствуют режимам резонанса токов.

В качестве иллюстрации сформулированного правила исследовяная постршм

частотные характеристики X=/(tti) и b=f(ut) длг ----- по .

определнм. какие резонансные режимы и в каком

гри изменении частоты от О до оо. Для двухполюсника рнс. 3.28. ж реактивное сопротивление равно сумме реактивных сопротовлений двухполюсников рис. 3 28 а г. В ссхтаетстеии с этим ординаты кривой Х=/{ш) для схемы рнс. 3.28, ж полу-чаем на рис. 358. э г>тем суммирования ординат кривых Х=/ fe) рис. 3.28, б, д. Зависимость й=/И для схемы рис. 3.28. ас изображена иа рнс. 3-28. . Из рис. 3.28. 3, и ввдно. что в схеме рис. 3.28. ж при увеличении частоты от О до происходит следующее: при и=ь) возникает резонанс напряжений, при -

резонанс токов, затем при ©=Ша вновь возникает резонанс напряжений. При гослвдуияцем увеличении частоты резсиансю в схеме возникать не будет,

схватим внимание на следующее:

IJ режкмы резонанса токон я резонанса напряжений чередуются;

2) число резонансных частот для канонических схем (см. § 3,31) ( меньше числа реактивных элементов;

3) если в, схеме есть путь для прахс№девия постоянного тока, то при ллаа-ном увеличении часюты первым наступит резоввис токов, если нет-ркзонаис гапряженнй.

Это следует из того, что если есть путь дли-постоянного тока, то при ю=0

характеристика X ,) иачинается с нуля, а Затем увеличивается (\> oj и

ври некоторой о гретч>певает разрма, кот<Ч)ЫЙ и соответствует резонансу токов, ппи =, =. ,. -. .-------. резонансных---------------------

ение его следует представил, в виде отношения двух пода-. т. е. Х=Л/(Ц И(Ц. Корни уравнения /U(w)=0 соотййР сгвуют частотам, при которых возникает резонвис напряжений. Корни уравнения МЩ=0 соответствуют частотам, при которых имеет место резонанс токов.

§ 3.31. Кэ!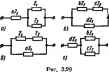

кие схемы. Экшвалаппые двухполюсники.

Путем эквявалапных преобразований отдельных частей сложных схем доследнне можно Гфивести к gijge простым схемам с ми-нималыю возможным числом R L, С в них -к каноническим схемам. Так, схемы рйс. 3.2S являются каноническими. Преобразования осуществляют либо путем перехода от звезды к треугольнику (или насйорот) или от параллельно-последовательного соединения (рис. 3.29, а) к параллельному (рие. 3.29, б), либо от параллельного соединения (рис. 3.29, в) к последэвательно-параллельному (рис. 3.29, г) и последующего упрощения схемы. Значения коэффициентов перехода: для рпс. 3.29,о.б й=с(1-Ьс); c==(l+af; rf=l-f-o; для рис 3.29.е.г Ь = ; c{iJ * = ТТ-

Двухполюсники рис. 3.29. о, б, как и рис. 3.29, в, г, называют дкеиеалеигпиыми, так как они имеют равные входные сопротавления при всех частотах.

§ 3.32. Передача энергии от активного двухполюсинка нагрузке.

К зажимам аЬ активного двухполюсника рис. 3.30, а подключена нагрузка 2 = J? +jX . Требуется выяснить, при соблюдении каких условий в нагрузке вьлделяется максимальная активнан мощность.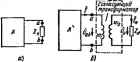

По методу эквивалентного генератора (см, § 1.25), ток в нагрузке

Д Zb,=i/?bi+;.?bi -входное сопротивление двухполюсника по отно-и1ю к зажимам аЬ.

По условию, R и Х заданы и изменить их нельзл Изменят можно лишь Я и Х . Выберем такое чтобы т<ж в цепи бьи максимальным; это возлгожно, если Хд-{-Х = 0. При этом двухщ*; люсннк работает в резонанспом режиме -ток через нагрузку поф совпадает с напряжеиием ОоЬуУ-

Как и в цепи постониного тока (см. § 1.25), если взять R =R\ выделяющаяся в нагрузке мсяцность максимальна:

/п,ех-1/гЬ.../(4/?ьЛ.

Таким образом, чтобы выделить в нагрузке, присоединяемой к аь-пюному двухполюснику с входным сопротивлением /в. + /вк. максимально возможную мощность, необходимо выбрать следующие сопротивления нагрузки: Л =-и R = Rb.

% 3.33. Согласующий трансформатор. Нагрузкой двухполюсника ыожет быть какое-либо уже существующее устройство, сопротивление которого 2и, так же как и входное сопротивление двухполюсника Z задано и не может бьт, изменено. В этом случае согласование нагрузки с двухполюсником осуществляют, ирнсоеданяя иагру:1ку не неносредственно к зажимам двухполюсника, а через согяасукищй трансформатор в соответствии со схемой рис. 3.30, б. Обозначим через Wi и w. число витков цертичной и втхричной обмоток трансформатора. Активные сопротивления и индуктивности рассеяния обмоток полагаем весьма малыми и при расчете не учитываем. Сердечник трансформатора (иа рисунке не показан) выполнен из высоксжачест-венного магнитного материала с малыми потерями, поэтому тсж холостого хода трансформатора мал по сравнению с током по обмотке при нагрузке. Такой трансформатор по своим свойствам приближается к трансформатору, который называют идеальным (см. § 3.34), Для него справедливы соопюшения (обозначения соответствуют рис. 3,30, б)

Пояснения к этим формулам см. в § 15.67 (обозначе1н1я соглас)ются так: и ь = 1. h = h / = Входное сопротналение изображенной пунктиром части схемы по отношению к зажимам аЬ

в соответствии с предыдущим это сопротивление должно быть ¥хтА плексно-сопряженное с сопротивлением двухполюсника:

Отсюда следует, что для выполнения условия согласования й активному сопротивлению Рв: = К {щ/щ/, а для согласования по реактнвнсму сопротивлению А.- (ш/кг)*. Отношение чисел

передачи энергии

швтяов WiIWi определим из первого условия WiIwVKjK- При боре числа витков и , и площади поперечного сечения сердечника трансе - должно быть учтено, что в установившемся режиме

габоты амплитудное значение потока в сердечнике ие должно дости-потока насыщения этого сердечн1та, иначе будет нарушено условие /iiwi -A.jO- Д-я выполнения согласования по реактивному (дапротиалениго поьтедовательно с нагрузкой включают дополнительное реактивное сопротивление соотвегствующе1хэ характера.

§ 3.34, Идеальный трансформатор. В качестве злеменгсв схем замещения электрических цепей нарвду с R L, С, М в литературе используют идеальный трансформатор (ИТ).

Идеальным называют трансформатор без потерь, у которого входные н выходные токи и напряжения связаны соотимиениями f/, = где /C = ai/Kjj -кшффнщкит трансфорлацни. Идеальный трансформатор трансформирует напряжение в напряжение ба, ток /, в ток /j, сопротивление нагрузки Z в сопротивление юг (см. § 3.33).

§ 3.35. Падение и потери напряжения в л

Генератор соединен с приемником энергии линией передачи,которая обладает активным fi.i и иидук-тчаныы X =iiiL сопротивлениями.

Построим векторную диаграмму для цепи, состоящей из генератора, линии передачи и прнем-ннка. Для определеиноста положим, что нагрузка приемника имеет индуктивный характер. Вектор напряжения в конце ляннн (нв приемнике) напра-анм гроизвотьио (рис. 3.3J), ток / отстает от него в силу нндуктннного характера нагрузки. Падение напряжения в активном сопротивлении линии /Rj, совпадает,по фазе с током, падение напряжения в индуктивном сопротивлении лиинн Xj, опережает тох на W.

Пол тюдеииш напряжения в линии передачи понвмают модуль геометрнчеетяД разности векторов папряжсния в начале и конце {О линии: /] ?ii-(-(toLj,)*.

Потеря напряжения в линии передачи равна разности модулей напряжения в начале и конце ливни, т. е. \Ui\ - \CW. Потеря напряжения показывает, на сколько вольт напряжение в конце линии меньше, чем напряжение в начале ли-ннн. Как правило, падение напряжения больше потерн наиряження.

§ 3.36. Расчет электрических цепей прв наличии в них магнитносвязанных катушек, В состав электрических цепей могут входить катушю], магнитносвязаиные с другими катушками. Поток одной из них пронизывает другие и навод1ГТ в них э. д. с. взаимоиндукции, которые должны быть учтены в расчете. При составлении уравнений для магнитносвязанных цепей необходимо знагь, соглаош или встречно направлены потоки caMomijuHH и взаимотшдукции.

Правильное заключение об этом нож1ю сделать, если известно Направление намотки катушек на сердечнике и выбрано положитель-вое направление токов в них.

На рис. 3.32, а катушки включены согласно, иа рнс. 3.32, б- Цречно. Чтобы не загромомадатб чертеж, с<рдс 1иики катушек на

Рис. 3.31

электричеадих схемах обычно ие изображают, ограничиваясь тем, Оцноим(Ш1ые зажимы (например, начала катушек помечают i выми значками, например звездочками *.

Схема рис. 3.32, в эквивалентна схеме рис. 3.32, а, а рис. 3.32, г-схеме рис. 3.32, б.

Если на электрической схеме токи двух магнитносвязанных вп шек одинаково ориентированы относительно одно1ша!но (зве1дочкам1 обозначешых зажимов катушек, например оба направлены к звезд;] кам или оба направлены от зязездоче4, то имеет место согласное i ченне, в противном случае -встречное.

е) г)

Рис. 3.32 Рис. 3.33

На примере рис, 3.33 рассмотрим методику составления для расчета нагаитносвязанных цепей. Произвольно выберем жительные направления тсжов в ветвях схемы рис, 3.33, Направлени обхода контуров выберем по часовой стрелке. Сначала составим ур нения для мгновенных значений:

для левого контура (первая и втекай ветви)

Перед слагаемым М поставлен тот же знак, что и перед так как ток ii и ток (з входит в однопмшные зажимы магнитносВ! занных катушис. т. е. имеет место согласное включение. Сумма с гаемых l + L, представляет собой падение напряжения в i ной катушке.

Все слагашые левой части уравнения (а) взяты со знаком п.т так как на всех участках первого контура положительные nanpmi ВИЯ токов совпадают с направлением обхода контура.

Составим уравнение для правого контура (вторая и третья Направление тока встречно направлению обхода контура, i сумма падений напряжений во второй ветви войдет в уравнение

Одной! звездочек

и конец размечают для каждой пары катушек отдельно.

э обозначают в катушек, то в

знаком минус:

В комплексной форме записи

М-Л(/? -)+/а(Кз+Мз) = Д. (г)

Последовательное

катушек. На рис, 3.34 изображена схема шследовательного соглас-

Рис. 3.34

Рис. 3.35

ного включения двух катушек, а иа рис. 3.35 - гюслецовагельного встречного включеяия тех же катушш. Пр! согласном шлючении

В кшплеююй фс5)ме записи

2сог. = (L,+L,+2M). (3.54)

Векторная диаграмма для согласного шииочетня изображена иа рис. 3.36, где f/i -напряжение иа первой катушке; й - т второй. При встречном включении

Z. =Ri+R.+/o(i.+i,-2M)- (3.56)

Векторная диаграмма для встречного включения при и

Хй>М изображена на рнс. 3.37.

Отсюда где