такого двухполюсника понимают режим (режимы), при котором ное сотфотивлеиие двухполюсника ивляется чисто активным *.

По отношению к внешней цепи двухпатюсник в резонансном режиме ведет себя как активное сопротивление, поэтому- ток и напряжение на входе двухпадюсиика совпадают по фазе. Реактивная мощность двухполюсника при этом равна нулю.

Различают две основные разновидности резонансных режимов:, резонанс токов и резонанс напряжений.

§ 3.26. Резонанс токов. Явление резонанса в схеме 3.25, а, образованной двумя параллельными ветвями с разнохарактерными реактивными согфогавлеииями, назыпа[()т резсштат токов.

Пусть первая ветвь имеет активное сопротивление Rt и индуктив- ное b>L, а вторая ветвь -акт1шное R2 и емкостное 1/соС.

Ток li первой ветви отстает от напряжения tj ~ 0 i, (рнс. 3.25, б) и может быть записан как

/i=Ki = f/(,-,-fca

Ток /в второй ветви опережает напряжение:

Тсж в неразвегвлешюн части цепи

/=A+/.=(g.+g2)-j(fci+fc. По определению резонансного режима, ток / должен совпадать во фазе с напряжением О. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю:

В соответствии с (3.36)

Следовательно, условие наступления режима резонанса токов в схеме рис 3.25, а можно заппсааъ так:

I- PJS.).

На рис. 3,25, б изображена векторная дваграмма для резонансного режима. Из (3.51) следует, что если /?2 = 0, то резонанс наступит при

(3.51-)

В еще более частном случае, когда R = 0 и i?i<toL, резонанс наступит пра

MLCfl. (а5П

СМятэтельн), дл} определения условий наступления резонанса следует приравнять нулю мнимую часть комплекса елодногосопротввлеиив двухполюсник*

резонанса можно достичь путем изменения ю, L, С или i?, и Rg. Ток в ие1)азвегвлещной части схемы по величине может быть меньше, * токи в ветвях схемы. При i?a = 0 н J?i!0 ток / может оказаться д1(чтожио малым по сравнению с токами /. и /а-

В идеализированном, практически ие выполнимом режиме работы, когда

О, ток в неразвётвленной части схемы 3.25, а равен нулю и входное сопрошвлениесхемы равнобескоиечносги. Обратим внимание на следующее, В

формулу (3,51) входит пять величин (L, С, Ri, R%, Если определять из нее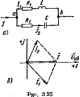

t или с, то может оказаться, что для искомой величины будут получены одно или два дейсгетгтелыщх значения либо мнимое значение.

Получение двух №ч1ствительных значений для L и с свидоелыпвует о том,

что при неизменных четырех параметрах вцледствне изменения пятого параметра можно получить два резонансных режима (пояснения к возншокшепию двух реэонаипшх режимов при изменении одного параметра и неизменных осталыплх даются в примере 54).

Получение мнимых значений L и С свидетельствует о том, гго при данных сочетаниях параметров резонанс невозможен.

Опреде,1им и из (3.51):

где И(, - резонансная частота в контуре без потерь при J?, = /?g = 0.

[Ъскальку угловая частота дейсгиггепьна и по.тож1гтельна, то числитель и знаменатель формулы (а) должны быть с одинаковыми знаками. Это имеет место при:

а) >Щ и ->й;; б) ~<Rl и <?S.

При R,=R частота При L/C=Ii = Ri

(o = (i)ol/Q/0, (б)

т. е. 6 в случае (6) получается величиной неопр(а1еленной. Физически это означает, что резонанс может возникать при любой частоте, противление паллельного контура при этом чисто активное, рав-

Пример 43. В схеме рис. 3.25, а Ri = 30 Ом; Ом; Яй=0;

ЮсЛ При какой емкое в схеме будет резонанс таков?

Решение. По формуле (3.51),

-с-т--:Х--0--

§ 3.27. Компенсация сдвига фаз. Входное сопротивление больший* ства потребителей электрической энергии имеет индуктивный xapaKiil Для того чтобы уменьшить потребляемый: ими ток за счет снижения его реактивной

составляющей н тем снизить потери энергии в генераторе и подводящих проводах, параллельно приемнику энергии включают батарею ксвщенсаторов.

Уменьшение угла сдвига фаз между напряжением на приемнике итоком, потребляемым от генератора, называют компенсацией сдвига фаз.

Компенсация сдвига фаз особенно существенна для энергоемких потребителе, иаярим крупных заводов. Осуществляется она Б месте ввода линии питания в распределительном устройстве. Экономически выгодно подключать юаденсаторы на возможно более высокое напряжение (ток через конденсаторы IcUaCj. Угол сдвига фаз tp между напряжением и током, потребляемым от источника питания, обычно ДОВОДЯТдо значения, рри котсром cos qi = 0,9-0,95.

§ 3.28. Резонанс напряжений. Резонанс в схеме последовательного

Рис. 3.26

соединения R, L, С (рис. 3.25, с) называют резонансом напряжений.

При резонансе ток в цепи должен совпадать по фазе с э. д. с, Ё. Это возможно, если входное сопротивление схемы

будет чисто активным. Условие наступления резонанса в схеме рис. 3.26, с

(flaL=l/(co,q.

(3.52)

где (йд-резонансная частота. i

V При этом / = EiR. Напряжение иа индуктивности при резонансе равно напряжению на емкости:

Опюшенве

(3.53)

ячывают дсротностью резонансного контура. Добротность показы-аег во сколько раз напряжение на иидуктивности (емкости) превы-ае напряжение на входе схемы в резонансном режиме. % i i В радиотехнических устройствах Q может доходить до 300 и более. Векторная диаграмма для режима резонанса нзо-бржжена на рт!с. 3.26, б.

Характериспитестм. сопротивлением р для схемы рис. 3.25, а называют отношение напряжения на L или С в режиме резонанса к току в этом режиме: p=QR.

§ 3.29. Исследование ра-6о+ы схемы рнс. 3.26, а при изменемн частоты и индуктивности. Пусть в схеме рис, 3.25, а параметры R, L, С к э. д. с. £ постоянны* но меняется частота т. Обсудим характер изменения тока / и напряжений I/l и [/с в функции от i

Ток в цепи

При изменении о меняется реактивное (

вленве цепи X =

= coL --г при ci)*->0 сопротивление X-> то и ток /- -0; при

(ol/iTC сопротивление Х = 0 в ток I = EiR; при со-> то сопротивление Л->то и ток /->0.

Напражение на индукгавностн

Vi. = iaU = E.-

При ю- -0 напряжение Ul = 0; при о-то напряжение Vi~>E (рис. 3.27, о). При Q>-p- кривая Vl (кривая Vq) проходит через

Максимум, При (?<:-р крнвая Vl монотонно стремится к Е.

При (0-0 напряжение на емкости с = 1- стрешгтся к Е, npi

V ваменяет слово естремшцнйся? или соответствеино стремится .

* Стрелкг

Из рис. 5.27, а видно, что максимумы напряжений на инд: ности Ul и емкости Ucjtu&m место при частотах, ие равных р ной частоте сод 1/У/,С: максимум t/i имеет место при частотео)>. а максимум Uc - npH частоте

На рис. .27, б изображены две кривые, характеритощне за; симость I=f(ai) для цепи с неизменными L, С к Е пртдвухразл ных значениях R. Для кривой 2 сопротивление R меньше (а доб> ность Q больше), чем для кривой 1.

Обычно кривые рис. 3.27, б изображают в огаоснгельных цах, откладавая ток в долях от тока при резонансе, а частоту в долях от резонансной частоты. Графики тока в относительных еу. нинах изображены на рис. 3.27, в. Они построены по формуле

Чем мевыпе активное сопротивление резонансного контура неизменных остальных параметрах схемы, т. е. чем больше добр- т ность контура Q, тем более острой (пикообразной) стансеится фори кривой /=/Н.

Полосой пропускания резонансного контура называют полосу част cujj -Oi = K)o/Q, иа границах которой отношение составляет 0,707 (рис. 3.27, в).

Граничные частоты *>д.й (V 14-4Q ip l).

Если в схеме рис. 3.26, а менять ие частоту, а индуктивность L то зависимости /, Ui в функции от Л£ = toL (о = const) будут в внд-а кривых pic. 3.27, г.

Так как ic--f. а l/coC=const, то кршая Vc=f{iiil) кaчec

венно имеет такой же вид, что и кривая / = f(toL).

Пример 44. В схеме рис. 3.26,а ;=ШОм; L = l Г; С=1мкФ Определить резонансную частоту щ, добротность Q, атакженапрк

жение иа емкости Vc, еслн на вход схемы подано напряжение 10 mi

прн резонаншой частоте.

Решение. Резонансная частота со 1/1/1С= 1/УТ0= = 10 Добротность (3(©Д-)/ = (10-1)/10-100. Ток в цепи IE/R

= 0,01/10=1 мА. Напряжение иа емкости UcQE = 100-0,01 = 1

§ 3.30 Частотная характеристика двухполюсника. Входное соптй тивленне двухполюсника и его входаая проводимость есть тащо частоты. Зависимости действительной и мнимой частей входного тивлення или входной проводимости двухполюсника от частоты вают частотными характеристиками двух/юлюсиика.

Чясютные характертстики рассчитывают, если известшл схема .hvtShhhx соединений двухпсшюсника и значения активных сопро-ний, индуктивиосгей и емкостей в ней. либо снимают опытным

снятии часгошых характеристик опытным путем на вход ,vfMH подают напряжение, частота которого может меняты:я широких пределах, и по результатам шмереянп подсчитывают действительна и мшшую части входного сопротивления.

В схему двухполюсника могут входить последовательно н парал-jbHO соединенные ицдуктнБНОСТн, емкости и активные сопротивления Наибольший интерес представляют частотные характеристики двухполюсников, составленных только из индуктивностей и емкостей.

Если частота источника питания двухполюсника высока, то индуктивные сопротивления катушек индуктивности оказываются много больше собственных активных а)противлеш1й катушек и для упрощения построения частотных характерисгак последними часто пренебрегают. Для такой идеализированной упрощенной схемы, где нмаотся только индуктивности и емкости, построение частотных характеристик схемы упрощается.

Рассмотрим построение частотных характеристик двухполюсников, изображек-иых на рис. 3.28, о, г. Двухполюсник рис. 3.28. а образован последовательно соединенными Ц и С, двухполюсник рнс. 358, е-параллельно соединенными в Cj. При построении частотных характеристик будем полагать, что в реактивных солротнвлениях всех элементсв, из которых составлены двухполюсники, отсутствуют потери энергии. Входное сопротивление и Bxo;uiafl проводимость для двух- мксщка ррс. 3.28, а соответственно:

o)Li-(1/иСО*