Поскол№у первый и второй законы Кирхгофа справедливы и j цепей синусоидального тока, то можно было бы записать уравнен для мгновенных значений величин цепей синусоидального тока, i реши от них к уравнениям в комплексах и затем повторить тл всех формул гл. 1 для цепей синусоидального тока. Понятно, проделывать выводы заново нет необхощ1мостн.

В том случье, когда отдельные ъетви электрической цепи cnmvi идалыюго тока не связаны между собой магнитно, все расчет и формулы гл. 1 пригодны и для расчета цепей син>Соидального ток! если в этих формулах вместо постоянного тока / подбтавить компле тока /, вместо проводимости g -комплексную проводимость V, вм-с сопротивления -комплексное српрогавление Z и вместо посюявв э. д. с, £ -комплексную э. д. с. Е.

Если же отдельные ветви электрической цепи синусоидально тока связаны друг с иругом магнит1Ю (это имеет место при налич1 взаимоиндукции), то падение напряжения на каком-либо участке neiiJ зависит ие только от тока данной в но и от токов тех ветвей, с koi данная вегвь связана магнитно. Ра электрических цепей синусоидального т ка При наличии в них магнитносвяза , пых ветвей приобретает ряд особеииоапейЛ которые не могут быть учтены, если г формулах гл. I непосредствен1Ю замавщ Е ка Ё, R aaZ ug на Y. (Особенносга расчета магнитносвязанных цепей рас смотрены в § 3.34.)

§ 3.(8. Применение векторных j грамм при расчете электрических цеп) синусоидального тока. Токи и напряжения на различных участках электри-J ческой цепи синусоидального тока, к правило, по фазе ие совпада1от. Harju ное представлешю о фазовом расположении различных вектсов t векторная диаграмма токов и напряжений, Анал(ггические расч-. ъ электрических uenfti синусоидального тока рекомендуется conpcwaffi дать построением векторных диаграмм, чтобы иметь возможность качественно контролировать эти расчеты.

Качественный контроль заключается в сравнении направлений раз-, личных векторов на комплексной плоскости, которые получают прн.-аналитическом расчете, с направлением этих векторов, исходя из фвг: зячЕских соображений.

Например, на векторной диаграмме напряжение на ннд-ктнвностн Ol должно опережать протекающий через нее ток на 90°, а напрн- [ жение на емкости Сс-отставать от протекающего через нее ток иа 90°,

Если аналитический расчет дает результаты, ие совпадающие, с такими очевндныып положеикямн, то, слецователыю, в него вкрз-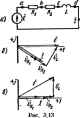

. дапбка Кроме того, eeKTOjwyro диаграмму часто используют и с соедсгво расчета, например в методе пропорциональных величин. Поювд! 31- В схеме рис. 3.13,о заданы: c=I41srao)f В; R, = tWiSOM; /? =2 Ом; /.0,00955 Г, Угловая частота .u) = 3l4c- . * Препияпъ ток и напряжение иа элементах цепи, е решение. Запишем уравнсЕше для мгновенных значений:

дд)ейдем от него к уравнешпо в комплексах;

I(Rj-\-Ri)iaLiE или IZ = E, где г = -fB + / i- - 3 -f 2 -f /314 0,00955 = 5 + 3/ = 5.82е/з i*. Комплекс действующего значения э. д. с.

£=141/12=100 6.

/ = f/Z=100/5,8e3i°= 17.2е/з А.

Напряжения на сопротнвлегаш Ri

(JRUbtlRi-blfiQ-rii В,

на сопротввлении

f? , = i/e,= /Ws=34,4e-3* В;

. на ивдуктивносга

Ot = 0,a = i<oLt=3i.n,2e-f5lSel В. Векторная диаграмма изображена на рис. 3.13,6, Вектор Ё направлен по оси -J-1, Ток отстает от него на 31 .

Пример 32. Решить задачу примера 31 методом пропорциональных величин.

Решение, Зададимся током в цепи в 1 А и направим его на векторной диаграмме рис, 3,13. в по оси -f I (/ = 1), Напряжение на активном согсггнвлении Rt совпадает по фазе с током и численно равно 1-3 = 3 В. Напряжение на R также сов[[адает с током и .f- Напряжение на индуктишкхти равно 3 В и опережает ток на У(Г, Из Прямоугольного треугольника следует, что при токе / = = 1 А на входе £=1/5--f 3 = 5,82 В

Так kiiK на входе действует э. д. с. в 100/5,82= 17,2 раза болыие, то все токи и напряжения дапжны быть умножены на коэффициент Д- На рис. 3,13, в все векторы повернуты на ЗГ против часовой Релки по сравнению с соответствующими векторами на рис. 3,13,6. ие нзмен° расположенве векторов ка диаграмме прИ этом

Пример 33. В цепи рис. 3.14,о i? = 4 Ом; со=1№ с-, Опреде-5 = 2 д У Рмкоста С, если при э. д. с. £ = 10 мВ ток в цепи

Решение. Комплаадюе сопрсггивленне цепи 2=R-егоч

дуль 2 = VR* + (l/wC)s.

По закону Ома, / = £/г. Отсюда г Е = 10 -10-/2 - IQ- 5 С

Следовательно, Хс= 1/(оС=Кг=-К= = / 5-4==3 Ом; = l/(coXc) = l/l№-3 = 3.33 мкФ.

Векторная диаграмма изображена на рис. 3.14,6.

Пример 34. На участке об развегвлшной цепи рис. 3.15, й г лельно включены и1[дуктивное сопротивленце Xi = o}L и aKTHBt противление R, численно равное Х. Показание амперметра 5 А, Огфеделтъ показание ампдэметра Д, полагая сопроти! ампиетров настолько малыми, что их можно не учтывать.

Решекне. На рис. 3.15,6 качественно построим векторнуюдиа4 грамму. Напряжение Ot совпадает по фазе с током /j. Ток /, ( стает от тока Д на 90° и равен ему по величине- Ток в jiepaanei ленвой части схемы /s = i + 4. Мод)Ль тока /зравен 52= 7,05 А. 1 Амперметр Д покажет 7,05 А.

Пример 35. Построить векторную диаграмму токов к напря для схемы рис. 3.16, а, если ток /,= 1 А, 10 Ом; c.Li= 10 Ом;Ч 1/шС=14,1 Ом; 0)1,3 = 20 Ом и /?э = 2,5 Ом.

Решение. Обозначим токи м выберш положительные напр; ния для них в соответствии с рис, 3.16, а. Выберем масштаб для т /Л/= 0,5 Д/см и для напряжешй та -4 В/см. Ток Д направим п;-оси +] (рис. 3.16,6). Падение напряжения [}r, = 10 В и пО < совпадает с током /,. Падение напряжения в индуктавном сопро лении oiL также равно 10 В, но опережает ток Д на 90 . Геометри- ческая сумма Vfi,-\-lJt, по модулю равна 10]/ 2=14,1 В. Емкостный J ток /g опережает это напряжение на 90°. Модуль тока L = = 14,1/14,1 =?1 А.

Ток в ны1азаетвленной части цепи равен геометрической -- . токов: /з=/ + /2. Модуль его равен 0,8 А (найден графически).! Падение напряжения на сопротивлоаш Rs равно 2 В и совпадаетпоЧ фазе с током /з. Падение напряжения на индуктивности Is опережает J ток /з иа 90° и численно равно 0,8-20= 16 В. Напряжение на вxoйl схемы равш а. д. с, и составляет около 18.3 В.

Р Qfi Решить задачу, обратную рассншренион в примере 35.

С-Пример 36- Решить зад. нтлвны значения токов /.

сшт Паяным (ПО s a- ч-ех ксв и трех напряжений) оить векторную днаграш.у.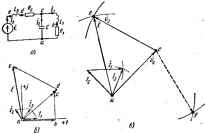

Решение. На рнс. 3.16,е отложим вектор Ос, по модулю равный 14,1 В. Для сопоставления с рис. 3.16, 6асполож ш его на диаграмме так же, как он расположен иа рис. 16, 6.

Изобразим на диаграмме ток Он на 90 опережает напряжение Ur и по модулю равен 1 А После этого построим на диаграмме токи /j и /я, воспользовавшисъ тем, что три тока (Д, 4 и /а) образуют замкн>тый треугольник (рис. 3-16,6).

Для построения треугольника по трем сторонам fr. е. фактически ДЛЯ определения третьей вершины ею) из котца тока (из одной вершины треугольника) проводим дугу радиусом, равным току Д, а нз начала тока (т. е. из второй вершины треугольнти) проводим УТ, радиусом, равным току /,.

Точка пересечения этих дуг даст искомую третью еерш]шу тре- льннка, т. е. точку, в которой оканчиваются векторы токов Д

i- После того как на диаграмме отределено. патоженне тока ij,

но изобразить на ней векторы напряжения и э. д, с Ё,

Напряжения Ос, Os н э. д. с. Ё также образуют замкнутый угоо1ьник. Его построение осуществляется аналогично построению угольника тсжов.

Из конца вектора Uc проводим дугу радиусом, равным I/3, а , начала вектора (7с-дугу радиусом, равным Е. Дуги пересекаются в двух точках си/..

Так как напряжение U3 представляет собой падение напряжения от тока /з на последовательно соединенных Rs и Ls, то оно по фат должно опережать ток /g, а ие отставать от него.

Поэтому из двух точек {е и /) выбираем точку е (если бы выбралН точку /, то в этом случае напряжение бз -пунктир на рис. 3.16, е--отставало бы от тока /3, а ие опережало его).

В заключение отметим, что в, треугольнике токов дуги тоже пересекаются в двух точках, но вторая (лишняя) точка на рис. 3.16, й ие показана.

§3.19. Изображение разности потенциалов на комплексной пло- скости. Потенциалы цепи переменного тока являются комплексными числами. На комплексной плоскости комплексное число можно изображать либо точкой, координаты которой равны действительной и мнимой частям комплексного потенциала, либо вектсром, направленным от начала координат к дайной точке плоскости.

На рис, 3.17 представлены два вектора, изображающие собой комплексные потенциалы:

ф = -2+5j и фь--4 + /.

По определению, рность потенциалов Оаь = = Фо --6-f4/; Оа изобразится вектором, направленным от 6 к о. Первый индекс у напряжения (в нашем примере индекс а) указывает, к какой точке следует направить стрелку вектза напряжения. Ествлвенно, что

% 3.20. Топографическая диаграмма. Каждая точка элоарической схемы, в которой соединяются сопротивления, имеет свое значение комплексного потенциала.

Совокупность точек комплексной плоскостн, изображающих комплексные потенциалы одноименных точек электрической схемы, называют топографической д1юграммой.

Термин топографическая объясняется тем, что диаграмма напоминает топографическую карту местности, где каждой точке меспюсш отвечает определенная точка карты. Расстоиние между двумя точками иа местности можно определить, измерив расстояние между одноименными точками иа карте.

Аналогичные измерения можно проводить и на топографической диаграмме- Напряжение между любыми двумя точками электрической схемы, например между точками а и 6, по величине и направлению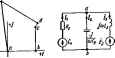

Рис. 3.19

1ределяется вектором, проведенным на топографической диаграмме точки Ь к точке с.

При построеини топографической диаграммы, как н потенциальной /см. § потенщ1ал любой точки схемы может быть принят рав-

ным пулю. На диаграмме эту точку гюме1цают в начало координат. Тогда положение остальных точек схемы иа диаграмме определяется параметрами цепи, э. д. с. и токами ветней. Рассмотрим примеры на построение тсаюграфической диаграммы.

Пример 37. По данным примера 35 построить топографическую диаграмму для схемы рис. 3.16,о.

Решение, Обозначим буквами й, 6, с,... точки схемы рис. 3,16, й, которые хотим огобраЗ{ггь на топографической диаграмме. Примем потенциал точки а равным ну.то: фд-О.

Выразим потенциал точки Ь через потенциал точки д: Фб = % + /1 1 = Ф +10. Знак плюс перед слагаемым itRi обусловлен тем, что при переходе от точки а к точке Ь перемещшие. происходцт навстречу теку /1 (при этом потенциал увеличивается на /К,), Точка Ь на диаграмме имеег координату по оси абсцисс -f 10. Аналогично, 4. = *t + /i/ Lx=10+/10: Фй=Фс+Л з:

Совокупность точек а, Ь, с, d, е на ксьшлексной плоскости рис, 3,18 представл)[ег собой топстрлфича-кую диаграмму для схемы рис. 3.16, а. По ней удобно определять напряжение между любыми двумя точками схемы и сдвиг по фазе этого напряжения по отношению к любому . Другому напряжению *.

Пример 38. Найти токи в схеме рис, 3.19 методом двух узлов. Положите.ть.чые направления , д. с. указаны на схеме стрелками: 4mY2smiat В; fa= 100/ 2cos((o/-120°) В; R = 20m; l/toC,-= 10 Ом; (oL3 = 5 Ом.

Решение. Запишем э. д, с. в комплексной форме:

£i=120, Emi. Выберем положительные направления для токов в ветвях к узлу а. Определим проводимости ветвей:

Vi = l/Zi = 1/2 = 0,5 См; = l/Z = 1/-10/ = 0,1 / См; K3=I/Z3-I/5/=-0,2/ См.

Cicflyer иметь чесхой днагсаммой ч пило. нет.

d виду, что итахого врафическыо ш>добия между то электрической схемш, для которой она построена.

гаграфи ик пра-