снмвсшическнй, или комплексный, метод расчета цепей синусоидад ного тока.

Сущность спмволического метода расчета состоит в том, что при. синусоидальном токе можно перейти от уравнений, составленных длй? мгновенных значений и являющихся диф })ёренциальными уравиенняЛ [см., например, (3.29)], к алгебраическим уравпенням, составленный относительно кетяшежсов тока и э. д. с. Этот переход основан на том, что в уравнении, составленном по законам Кирхгофа для ycTaHOBS--J шегося процесса, лятювашое значение тока i заменяют комплекокЛй амплитудой тока / ; мгновенное зиачекве напряжения на активжя! сопротивлении R = Ri- коштаахзы Rl , по фазе совпадающим с током / ; мгиове1нюе - качение напряжения иа индуктивности ut = = L - комплексом ImifL. опережающим ток на 90°; мгновенное значение иапрнжсння на емкости ыс = j[ id/-комплека ! я). отстающим от тока на 90°; мгновенное значение э, д, с, е -комплексом £ . Справедтвостъ замены Ui = Lf на / /cuL следует из § 3.7 и 3.8.

В § 3.8 было показано, что амплитуда напряжения на индуктивности равна произведению амплитуды тока на Xt = aL. Множитель / свидетельствует о том. что вектор напряжения на индукпшности опережает вектср тока на 90°.

Аналогично пз § 3.9 l.,>ct, что амплитуда напряжения на емкости равна амплитуде тока, умноженной на Хс= I/toC. Отставание напряжения на емкости от протекающего по ней Рве 3.9 тока на 90° объясняет наличие множите-

ля -/.

Например, для схемы рнс. 3,9 уравнение для мгновенных значений можно записать так:

Запишем его в комплексной форме: Вынесем / за скобку: Следэвательно, для схемы рис. 3.9

(3.29)

(3.30)

(3.3))

Это уравнение позволяет найтн комплексную ампл1пуду тока яеоез кс 1Ш1в!Сную амплитуду э. д. с. £ и сопротивления пени R,

Л Метод называют сх1меолич&иим потому, что токи и напряжения за;да1яют их комплексными нзображсляями или символа.ми. Так, j/ 9To изображение или символ падения напряжения iR; i4>L} - изображение или aiMEiori падения напряжения на индуктивности ut =

j=zL: - / - изображение падения напряжения на кон;1сатора

§ 3.12. Комплексное стротивление. Закон Ома для цепи синуса-ядальяого тока. Миожит&ль R-\-fv)L~ в уравнении (3.30) представляет собой комплекс, имеет размерность сопротгалашя и обозначается через Z. Его называют комплексным сопротаелегакм:

Z - ze = R -1- /toL - . (3.32)

Как II всякий комплекс, Z можно записать в показательной форме. Модуль кошлексного сопротивления принято (Означать через г. Точку над Z не ц* потому что принято ставить ее только над такими комплексны! величинами, которые от(йражают синусоидальные 4*нкции време

Уравнение (3.30) можно записать так: / Z = f . Разделим обе его част на 2 я пдайдем от комплексных амплитуд и йщ к комплексам дейсшуншшх значений / и £:

/ = £/2. (3.33)

Уравнение (3.33) представляет собой закон Ома для цепи синусо-идаяьного тока.

В общем случае Z имеет некоторую дейсготельиую часть и неко-торую мнимую часть /Л;

ZR+iX, (3.34)

где /? -активное сопротивление; X -реактивное сопротивление. Для схемы рис. 3.9 реактивное сопротивление

§ 3.13. Комплексная проводимость. Под комплексной проводимостью Y понимают величину, обратную комплексному сопротавлению Z: Y = l/Z = g-,b = y-i4 (а35)

Измерякгт комплексную проводвихть в Ом* или сименсах (См). ir&ibHyw часть ее обозначают через g, мнимую-через 6, Так

g-ll>.

(3.33)

S=-i y-Vg+f- (3-36)

Если X положительно, то n b положительно, при X отрицательном b также отрицательно.

При использоиапии комплексной прсжодимосга закон Ома (3.33) зашкъшают так:

где /в -активная составляющая тока; Z-реактивная составляющая тока; О - напряжение на участке цепи, сопротивление которого рав1ю Z.

§ 3.14. Треугольник сопротивлений н треугольник проводимосгей.

Из (3.34) следует, что модуль комплекснсто сопротивления

гУЩ. (3.37)

Следовательно, г можно представить как гипотенузу прямоугольного треугольника (рис. 3.10) -треугольника сопротивлений, один катет которого равен R, другой X. При этом

tg<r=X/i?. (3.38)

Аналогичным образом модуль комплексной проводимости в соответствии с (3.36) Следовательно, j/есть гипотенуза прямоугольного треугольника (рнс. 3.11), катетами которого являются активная g и реактивная Ь проводимости:

tg<p=b/g. (3.39)

Треугольна сопротнвленпн дает графическую интерпретацию связи wejiyiy модулем полного сопротивления г и активным и реак-Т1гвнь1М сопротивленвямн цепи; треугольна проводимостей-интерпретацию связи между модулем полной про- , юдимосги у и ее актвной и реактивной составляющими.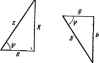

Рнс. 3.10

Рнс, 3.11

§ 3.15.-Применение логарифмической линейки для перехода от алгебраической формы записи комплекса к показательной и для обратного перехода. При расчете

яужно ммшюс э. л с. разделить ш комплекс сопротивления.

Из курса матшатики нзвесттю, что комплексное число можно представить в трех формах записи; алгебраической о+ /6, показательной и тригонометрической ccos ф-f/csinip.

Сложение двух и большего числа комплексов удобнее производить, пользуясь алгебраической формой записи. При этом порознь складываются их действительные мнимые часш:

( 1 + А) + ( 2 + /Ь + - = (а, + a,+a + j ф, + Ь~ 63).

Деление и умножение комплексных чисел целесообразно производить, пользуясь показательной формой записи. Пусть, например, нужно разделить комплекс с,е> на ксмплекс се* . В результате дел&ния будет получен комплекс

Модуль результирующего комплекса Сз равен частному c,/Cj -а аргумент ч<з = Ф, -Фа-

При умножении даух комплексов се и ci результирующий комплекс

cfiif* = Cje*<:/4 = Cjce ( л +ч К

При расчетах электрических цепей часто возникает необходимость в переходе от алгйранческой формы записи комплекса к показательной или в обратном переходе.

Удобнее это сделать с помощью логарифмической линейки.

Пусть задано комплексное число o-f /&. Из предыдущего (см. § 3.11 и 3.12) ясно, что а н & есть катеты прямоугольного треугольника, а его гипотенуза с=Уо* + 6. Частное-,от деления меньшего катета на больший катет дает тангшс меньшего острого угла прямоугольного треугольника, а деление меньшего катета на синус меньшего угла дает гипотенузу треугольника или моду-ль котпекса. Это и положено в основу определения модуля и аргумента комплекса по его алгебравческой форме а+уЬ с помощью логарифмической линейки. Движок линейки поворачиваем обратной стороной так, чтобы на лицевой части линейки нахсдилась сторона движка, на которой написано есинус н тзнгенс .

Последовательность операций нахождения аргумента и модуля такая:

1) значение меньшего катета откладываем по основной инжней шкале линейки и против него ставим риску визира;

2) значение большего катета откладываем также по осишной шкале н Против него ставим конец движка; так производится деление меньшего катета на больший;

3) по шкале тангенсов пропш риски визира отсчитываем значение наименьшего угла прямоугольного треугольника;

4) ие сдвигая визира, перемещаем движок так. чтобы против риски визира пришелся только что найденный угол на шкале синус ; так осу1црс1ш1яется деление меньшего катета иа синус меньшего угла;

5) модуль комплекса (гипспшуза , Прямоугольного треугольник отсчитывается Против конца шкалы движка по основной нижней шкале линейки.

Переход от показательной формы к алгейранческой совершэгя1Я в обратной последгшаггельности. Чтобы ие совериштъ ошибку при записи показательной ф<мы комплекса, рекомендуется сначала качественно изобразить заданный в алгебраической форме комплеке-J на конпла(сной плоскости, 4ttf ПОЗВОЛИТ правильно выразить угол между осью -j-1 и вектором через угол, наГйеиный по линейке. Углы, откладываемые против часовой стрелки от оси 4-1, считаются положнтельны--ми, почаажой стрелке- отрицательными.

Пример 30. Перевести в по- казательную форму следуияцие ксшшексы: а) 3-f 2/; б) 2 + 3/; в) 4-5/; г) -6 2/; д)-0,2-1-+0,4/1 с) 10-/0,8.

Решение, а) Ставим впзнр против цифры 2 на нижней пжале линейки и конец движка против циффы 3. По шкале тангенса находим угол 33°40. Передвигаем движок так, чтобы против риски визира на шкале синусов пришелся угол 3340. Отсчет по нижней шкале против конца шкалы движка дает модуль 3,6. Вектор 3+2/качественно изображен на рис. 3.12, о. Из рисунка вцдно, что угол между хью+1 и воггором равен 3340. Поэ1Х)му 3 + 2/= 3,6еззмо.

б) По линейке определим угол 3340 и модуль 3,6. Из диаграммы рис. 3.12,6 видно, что угол между осью +1 и вектором равен S0=-33°40 = 56°20. Следовательно, 2 + 3/-3,6е/5б20.

в) По линейке находим угод 3840* и людуль 6,4. Из диаграммы рис. 3.12,в видно, что вектор находится в четвертом квадранте. Угол меж осыо+1 и вектором равен -бГгс. Таким образом. 4-5/ =

г) По линейке определим угол 18°36 и модуль 6.32. Из диаграммы рис. 3.12. г видно, что угол между осью +1 и васгором может быть выражен двояко: либо как - П80-18°35)--16125, либо как-+ (180° + 18°3б) = 19835. Поэтому -6 - 2/ = 6,32е-Лб1-г5-

д) По линейке находим угол 2635 и модуль 0,448. Вектор находится во втором квадранте (рис. 3.12, д). Следовательно, 0.2 + /0,4 = 0.448ef 6°35. ,е

е) Этот случай принципиально отличается от рассмотренкых тем, что составляющие комп.ижа (катеты прямоугольного треугольника) П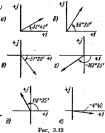

о абсолютной величине различаются более чем иа порядж. Причш гипотенуза прямоугольного треугольника практически равна боль-тему катету, а угол определяется по средней шкале движка. По лн-м-дке определим угол 4 40, который находятся в Етвергом квад-JaJre (рис. 3.12, е). Поэтому 10-/0.8= 10е- ° -.

§ 3.16. Законы Кирхгофа в символической форме записи. По

пм рму закону Кирхгофа, алгебраическая сумма мпювенных значе-вкйТОКОВ, сходящихся в любом узле схемы, равна нулю:

2* = 0. (3.40-)

Подсгаыш вместо (ь в (3.40) Де и вынеся е за скобку, получим е 2 Л = 0. Так как е* не равно нулю при любом (, то

£/.= 0. (3.40)

Уравнение (3.40) представляет собой первый закон Кирхгофа в символической форме зап1юи.

. Для замкнутого контура сколь угодно сложной электрической цепи синусоидального тока mojkho-составить уравнение по второму .закону Кирхгофа для мгновенных значений токов, напряжений н э. д. с.

njcTb замкнутый контур содержит п ветвей и каждая £-ветвь . в общем случае включает в себя э. д. с. сь, активное сопротивление ,

индуктивность я емкость С , по которлм протекает ток i*. * Тогда по иороыу закону Кирхгофа

Но каждое слагаемое левой части уравнения в соответствии с § 3.12 можно заменить на lZ, а каждое слагаемое правой части - на fj. Поэтому уравнение (3.4Г) переходит в

g/*Z.= ££,. (3.41)

Уравнение (3.41) представляет собой второй закон Кирхгофа в символической форме записи.

§ 3.17. Применение к расчету цепей синусоидального тока мето- Дов, рассмотренных в главе Электрические цепн постоянного тока . /*ля анализа н расчета электрических цепей постоянного тока разра- ан ряд меюдов и приемов, облегчающих решение по сравнению с решением системы уравнений при нспосрслсшениом использсеании аконов Кирхгофа. Из гл. 1 известно, что к числу 1аких методов относятся метод контурных токов, метод узловых потенциалов, метод * эквивалентного генератора и т. д. Известно также, 4to окончательные нечетные формулы этих методов пол>ча1сгт в результате выводсж, и основу Которых положены первый и второй законы Кирхгофа.