Решение, Для перехода от комплексной амплитуды к мгновенному значению надо умножить / иа и взять коэффициент прн мнимой части от полученного произвадения [см. формулу (3.106)];

I = Im 25е- lei = Im 25е < - =25 sin (wf - 30).

Под котлтхт дейспщющгго знтения тот, или под комплексом тока (комплексным током), / понимают частное отделения комплекс* иой амплитуды на >2:

пример 29. Записать выражение комплекса действующего значения 1Г(жа для примера 27, Решение,

/ = 8е- /К2 = 5,67е-20А.

§ 3.5. Спожение и i

-,ие синусоидальных функций времснм

с помощью комплексн! плоскости. Векторная диаграмма. Положим.

. что необходимо сложить два тока (£, и Q одинако-

I f вой частоты. Сумма их дает некоторый ток с той

же частотой:

и = /i.sin (<о1Ч-фО; и=1 sin

Требуется найти амплитуду / и начальную фазу ф тока i, С этой целью ток i, изобразим на комплекакда шюскосга (рис. 3.4) вектором /im= =/1 *. я токвектором /im = Bn* . Геомв** рическая сумма векторов /,я и im даст комплексную амплитуду суммарнош тока / -1. Амплитуда тока / {Н1ре№ляется длиной суммарного Рис. 3.4 вектора, а начальная фаза углом, образованным этим вектором н осью + Ь Для определения разности двух токов (э, д, с, напряжений) следует на комплекаюй плоскости произвести не сложение, а вычитание соотвегствуюкщА вектороа

Обратим внимание на то, что если бы векторы /, , /j и /, стали вращаться вокруг начала координат с угловой скоростью <о, то взаимное расположение векпв но отношению друг к другу осталось бы без изменений.

Векторной диаграммой называют совокупность вектюв на кош1-жкаюй плоскостн, нзображаюпщх синусоцдально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением Правильной ориентации их опюсительно друг друга по фаэй. Пример векторной диаграммы дан на рис. 3.4.

ч£. Мгновенная мощность. Протекание синусоидальных токов ®яиткам электрической цепи сопровоя(даегся потреблением энергии °**?чников. Скорость поступления энергии характеризуется моЩ;

ъю Под мгновенным значением мощности, или под мгновенной лл1Ы0, понимают произведение мгновенного значения нзпряже-*ина участке цепи на мгновенное значение тока i, протекающего да этому участку:

pul.

(3.13)

где р-функция времени.

Перед тем как приступить к изучению основ расчета сложных цепей синусоидального тока, рассмотрим соотношения между токами и напряжениями в простейших цепях, векторные диаграммы для них и кривые мгновенных значений различных величин.

Составными элементами цепей синусоидального тока являются активное сопротивление R, ицдуктнвиость L и емкость С.

Термин сопротивление! для цепей синусоидального тока в отличие от цепей постоянного тока недостаточно полный, поскольку сопротивление переменному тсжу оказывают ие только Рис, з 5 те элементы цепи, в которы выделяется энергия Б виде теплоты (их называют активными сопротш-ленияяч), ио и те элементы цепи, в которых анергия в виде теплоты ие выделяется, но периодически запасается в эпектричсском или магнитном полях. Такие элеакнтыцепи называют реактивными, а их сопротивления переменному току -рсиктаеншш сопротивлениями. Реактвнымн соп(ю влениями обладают ицдукпшжхгга и емкости (гюдробнее см. § 3,8 и 3.9).

§ 3.7. Синусоидальный ток в активном сопротивлении. На {Як. 3.5, а изображено акт1Юное сопротивление R, по которому течет ток i = / sm(o/. По закону Ома, напряжение

и = т=Н1 %тти

K = t/ sin*rf, (3.14

Комплекс тока / и совпадающий с ним по фазе комплекс напряжения и показаны на векторной диаграмме рис. 3.5, б.

На рис. 3.5, в даны кривые мгновенных значений тока , напряжения и и мощное

р = sin (О* sin (й< =- cos 2w0.

Мгновенная мощность имеет постоянную составляющую U /i я сосгавляютцую cos2u)f, изменяющуюся с частотой 2(а. П

требляемая от источника питания за время dt энергия равна р i

§ 3.8. Индуктивность в цепи синусоцдального тока. Практи г любая обмотка (катушка) обладает некоторой нцдуктнвностъю L аетивным сопротавлшием R. На схеме катушку можно предсгавн в виде последовательно соединенных тщуктивтосге L и сопротивления R.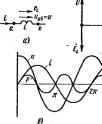

Вцделим из схемы одну индуктивность L (без актавногО сопр(-тивления)-рис. 3.6. а. Если через L течет ток i = / sin<of, в катушке наводшся э. д, с. самоиндукцгга

С£ = -J = - wL/ cos tof = tot/ sin ((Of -90°).

Гкшожитепыюе па1Ч)авленне отсчета для э. д. с. е,; на рис. 3.6, обозначено стрелкой, совпадающей с положительным иаправленга отсчета тока i.

Наем разность потенциалов шяеду точками а и 6.

При п)емш]№ии от точки 6 к точке а идем навстречу э. д. с. ez, роэтому (p = (p6-ei. Следовательно, D6=ip<.- P*=-e£=LJ

Положительное направление напряжсниц иь совпадает с положительным направлений! тока,

Из формулы =t.следует, что iгде r=UL-i

В дальпейшал индексы н и 6 у напряжения на ицщтсгивности (падения напряжения на индуктивности) ставить ие будем:

(( й = ы=-££. (3.15)

Следовательно,

и = sin (ttf + 90°) = V sin (ttf -1- 90°); (3.16)

Произведение tab обозначают Xl и называют индуктивным conpo-тиемнием:

XifoL: (3.17)

размерность его [XJ=(fi.H;q=c-i-OM-c-OM.

Таким образом, индуктивность оказывает переменному току сопротивление, модуль которого Xi = eiL, прямо пропорциональное частоте. Кроме того, напряжение на индуктивности опережает ток по фазе на 90 [см. (3.16)] -на рис. 3.6, б вектор напряжения О опережает вектор тока / на 90°. Комплекс э. д. с. самоиндукции El находится в противофазе с комплексом напряжения О.

Графики мгновенных значений i. и, р изображены на рис. 3.6, в.

Мгновенная мощность

p = ui = и cos mfsin 6)f=SMfL

sin2o>/

(3.18)

проходит через нулевое значение, когда через куль проходит либо и, либо (. За первую четверть периода, когда и и i положительны, р также положительна. Пло1цадь, ограниченная кривой р и осью абсцисс за это Бремя, представляет собой энергию, которая взята от источника питания иа создание энергии магнитиото поля в индуктивности. Во вторую четверть периода, когда ток в цепи уъкньшается от максимума до нуля, энергия магнитного поля отдается обратно источнику питания, при этом мгновенная мощность отрицательна. За третью четверть периода у источника снова забирается энергия, за четвертую отдается и т.д., т.е. энергия периодически то забирается индуктивностью от источника, то отдается ему обратно.

Реальная индуктивная катушка кроме индуктивности L обладает и активный сопротивлением R (рис. 3.6, г). Поэтому падение напряжения на реальной индуктивной катушке равно сумме напряжений на I и на Д (рис. 3.6. д). Как видно на этого рисунка, угол между напряженней t/ нэ катушке и током / равей SO- , причем tg6=R/(ci}L)= l/Qf где Qf-добротность реальной индуктивной кащшки. Чем больше Qj. тем меньше угол *.

§ 3.9. Конденсатор в цепи синусоидального тока. Если приложенное к конденсатору напряжение не меняется во времени, то заряд V=Ch наодной его обкладке и заряд-v=r-C на другой (С- емкость конденсатора) неизменны и ток через конденсатор не проходит {i=dqldt=-i)). Если же напряжение на конденсаторе меняется во >еменн, например по синусшдальному закову (рис. 3.7, а):

и = sin to/, (3.19)

я 63

то no синусоидальному закону будет меняться и заряд q кшденса-тора: д = Си = СиштЫ - ц конденсатор будет периодически перезаряжаться. Першдическая перезарядка конденсатора сопровождается npij>-. Тиканием через него зарядного тока ,

cs.Cl/ cos iii( = ii.a/ sin (ю(+9С ).е

(3.1П

Положительное направление тока через конденсатор на рис. 3.7, а совл падает с положтельным направле-имем напряжения. Из сопоставления (3.19) и (3.19) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90 . Поэтому на векторной диаграмме рис. 3.7, б вектор тока / опережает вектор напряжения V на 90°, Ампли- туда тока равна амплитуде напряжения (/я деленной на емкостное.

Дстаительно,

(3.20)

(3,21)

Емкостное сопротивление обратно пропорционально частоте и измеряется в омах. Графики мгновенных значений и, , р изображены на рнс. 3.7, е. Мгновенная мощность ,

puf=isiH2tof. . (3.22)

За первую четверть периода конденсатор потребляет от*йсточиика питания энергию, которая вдет на создание электрического пойя в конденсаторе. Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля, и запасенная в электри- ческом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода знергия снова запасается, за четвертую отдается и т, д.

Если проинтегрировать по времени обе части равенства

то получим

(3.23)

(3.24)

Равенство (3.24) позволяет определить напряжение на конденсаторе через ток по конденсатору.

йетсёальным и в ней нет потерь энергия. Однако при прнложеиии синус -нГального напряжения к пластинам конденсатора, разделенным твердым или яашким диэлектриком, в последнем всегда нмеютсп некоторые потерн внерган. Л5условленные вязким трением прн повороте днпольных модекзЛ, а также несо- ,;.,.рнством диэлектрика (наличием у него небольшой проводимости). Этн потери можно пренеечь. Если требуется у сть их

вершенством диэлектрик; ртдосительно малы, и

пасчете то киидеисатор заменяют схемой замещения (овс 3-7,е). В этой схеме параллельно емкости С присоединено активное сопротивление Ц, потерн энергии в котором имитируют потери энергии в реальном диэлектрике.

Ток / через конденсатор равен геометрической cj-mme npvjt токов: Тйка U через емкость, на 90 огерсжающсго напряжение О на кокаснсаторе (рис. 3.7. в), и относительно малого по величине тока /а через активное соп-иотименне R, совпадающего по фазе с напряжением U.

Таким образом,-ток через нонденсатор с неидеальным диэлектриком опережает напряжение на угол, много меньший Ж. Угол 6. ноторый с током Л. принято называть углом потерь. частоты и равняется в лучшем случае ескольким секундам, КИМ градусам. Всличниа tgfi дается в таблицах (ci свойства различных твердых и жидких диэлектриков

У

сорта диэлектрика и , в худшем-несколь-3), характеризующих Величину Q=(tg6)-* на-

§ 3.10. Умножение вектора на > и на -/ Пусть есть некоторый вектор .ДХе* (рис. 3,8). Умножение его на / дает вектор, по модулю равный А, но повернутый в сторову опережения (против часовой стрелки) по отношению к исходному вектору А на 90 , Умножение Л на - / поворачивает вектор Л на 90 в сторону отставания (по часовой стрелке) также без изменения его модуля.

Чт(йы убедиться в этом, представим векторы / и - / в показательной форме:

~f = l-c-i=e-t. (3.26)

Тогда

Aj - Aeel> = А (<.-t- °); (3.27)

-Aj = A-c-io=Ai<. (3.28)

Из (3,27) следует, что вектор /А, по модулю равный А, составляет с осью -h I комплексной плоскости угол фа+90°, т. е. ,повер-нут против часовой стрелки на 90 по отношению к вектору А,

Согласно (3.28), умножение вектора А иа -/ дает век-гор, по модулю равный А, но повераутый по отношению к нему на 90° по часовой стрелке.

§ 3.11. Основы символического метода расчета цепей синусоидального тока. Очень широкое распространение на практике iir>-