На провод-действует-механическая сила. Эта сила направлена противстюложно скорости v и стремится сохранить постоянство магнитного потока.

Формула (б) приближенна. Еслн учесть, что поттаосцегленне ионтура создано ие тольно внешним магнитным полем индукции В. по н током i, протекающим ко контуру, а также то, что с увеличением длины боковых сторон контура изме-вяется индуктивность L контура, то, по вторшу закону Кирхгофа,

Bb +L + i§ + iR=0. (в)

За положительное направление тока в формуле (в) принято иаправлмик против часовой стрелки, противоположное направлению для формулы (6J. Формула (б) следует нз (в), если второе и третье слагаемые формулы (в) по модулю много меньше первого К четвертого слагаемых.

§ 2.10. Емкость как параметр электрической цепи. Если между двумя прсводящвми телами У и 2, находящимися в диэлектрике с абссшнтюй электрической проницаемостью ft = 4, где efi = 8,86v X10 Ф/м -электрическая постоянная вакуума; е -электрическая проницаемость диэлектрика, сюдана разность потенциалов ij -Фа, то в пространстве, окружающем эти тела, существует электрическое поле (см. гл. 19). Поле в каждой точке характеризуется векторной величиной - напряженностью электричеснснто поля Е и скалярной величиной -потенциалом р (см. § 16.3). Размерности: [£] -В/м, [ф] -В.

Разность потенциалов между телами равна линейному интегралу от напряженносга Е между ними:

где Ш-элшент пути от тела 1 к телу 2 по диэлаарику. Вектор D = eJE называют электричшшм сжщением. Согласно теореме Гаусса (см. § 19.13), поток вектора D через

любую замкнутую поверхность S равен сумме зарядов v, окружев-

ных этой поверхностью:

где Й5~ элемент поверхности.

На рис. 2.9, а изображен цилиндрический кондЕисатор длиной I. На внутреннем электроде радиусом fi находится заряд q. на наружном электроде радиусом г -заряд -д. Пространство ии ; электродами заполнено днзлектриком, характеризующимся величиной е. Напряженность поля Е найдем по теореме Гаусса: Е = 4}/(2лв,г1).

Напряжение между обкладками конденсатора (рис. 2:9, а}

Под емкостью С между двумя телами понимают отношение абсолютной величины заряда v на одном из тел к разности потенциалов U между телами, обусловленной зарядом на этих телах:

Емкость цилиндрического конденсатора С = (2яе,/)/п. Емкость плоского кондшатора рис. 2.9, б C = eo£S/d.

Емкость -это параметр электрической цепи, характеризующий в интегральном смысле электрическое поле участка цепи (конденсатора). Она зависит от геометрических размеров и формы электродов, а акже

ИЛ 4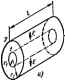

от электрических свойств среды между электродами конденсате От величищл напряжения U между электродами и величины заряда д емкость пе зависит (исключение составляют ковденсато1дл с сегнетоэ-лёктриком, когдв е зависит от £).

Емкость С измеряется в фарадах или в более мелких даницах микро-, нано- и пикофарадах:

1мкФ=10 Ф. lH0=lfr O. 1пФ-=10- Ф.

В электрическом поле конденсатяра запасается электрическая энершя

H7. = Cl 2 = v /(2Q. Т(ж (, протекающий через конденсатор при его зарядке, определяется скоростью изменения заряда:

. dq Cdu

dt--НГ-

Если заряд q по времени не изменяется, ток через конденсатор не протекает.

Положюелиые направления отсчета для тока i и напряжения иа конденсатсдж совпадают (рис. 2.9, е).

J. Какие Вам известны проявлений магнитного поля? 2. Запишите и

ментируите фориулу для наведенной э. д. с. 3. Что понимают под яв

само- и взавмонндукции? А. Данте определеине L и м. Как опрешуцт. L вН расетиым и опшиыи П)-г м,? 5. В опьпе Сшю получепо d Е 0,1 Г. М = 0.11 Г. Можно ли верить этим данным? 6. Какую роль вынолннют i. и Af KaJI элементы схем замещения реальпык электрически! цепей? 7. ОкормулирубИ принцип взаижпостн взаимнш ипдукц.и. 8. Дайте опрщелеике noH S викЙ1,.И

, . -, иаюг в курге алектртеских машин). Синусоидальные токя . и с ВЫСОКИХ частот получают с помощью ламповых или полу- иковых генератО10в (подробтю рассматриваемых в курсе радйо-и менее под1х>6но-в курсе ТОЭ). Принцип получения тусоидальной э. д. с. путем вращения витка с постоянной угловой !;оппстью в равномерном магнитном поле рассматривает :я в примере лпя о-С). Источник синусоидальной э. д. с. и источник синусоидального тока обозначают на электрических схемах так же, как и ииочннкя постоянной э. д. с. я тока, но над £ и /, ставят точки.

электркческие цепи однофазного сннусоиддлного ioka

§ 3.1. Синусоидальный ток н основные характеризующие его величины. Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):

< = / sin (~ + = / sin (ш( -t-if).

(3.1)

Максимальное значение функции называют амплигги/дой. Аыпли- туду тока обозначают / ; триод 7 -это время, за которое совершается одно полное колебание.

Часпюта равна числу колебаний в 1 с;

filT. (3.2)

Частоту / измеряют в герцах (Гц) или с*, угловую частоту i

рад/с или сг*. . -

- Аргумент синуса, т. е. ((of + iji), называют фазой. Фаза характе-;

рнзует состояние колебания (чнс-i лово значение) в данный момент мени t.

Любая синусоцдально изменяю-1 щаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.

В СССР II в Запад1юй Европе, р 3, наибольшее распространение полу-1

чили установки синусоидального тока частотой 50 Гц. принятой] Б энергетике за стандартЕ(ую. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень птрок: от долей герца, например в геологорамедае, до-миллиардов герц в радиотехнике.

Синусоидальные токи и э. д. с. сравнительно низких частот (до ] несколысих килогерц) подучакгг с помощью синхронных 1гнераторов j

источники

6 3.2. Среднее и действующее значения синусоидально изменяющейся величины. Под средним значением синусоцдально изменяющейся величины понимают ее среднее значение за полпериода. Так, среднее значение тока

/ Sin£i)fdl = -/m,

(3.4)

т. е. среднее значение синусоидального тока составляет 2/л = 0,638 от амплитудного. Аналогично, £,р=2е; Uf,2Ua.

Ширсжо применяют ионятве действующего значения ашусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока

/ = y-f 1= ]/Г J = = 0,707/ . (3.5)

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитуды. Аналогично.

£-£ Л2 и l/ = t/ 2.

Можно сопоставить тепловое действие сикусондального тока с тепловым действием постоянного тока / 0., текуш,его то же время по тому же сопротивлению.

Количество теплоты, выделенное за од1т период синусоидальным

Выделенная за то же время постоянным током теплота равна /посгГ. Приравняем их:

RI%г-

= Л/остТ или

Таким образом, дейспщтцге значение синусоидального тока / Численно равно значению такого постоянного тока, котсый за время, равное периоду синусмщального тока, выделяет такое же количестао теплоты, что и сикусоидзльный ток.

Большинство измерительных приборов показывает де значение измеряемой величины*.

§ 3.3. Коэффициент амплитуща и коэффициент формы. Ко- ;

циент амплитуды к - это отношение амплитуды периодически i няюш.ейси функции к ее действуюш,ему нию. Так, для синусоидального тока

Под коэффициентом формы кф понимают i . ношение действующего значения периодичес4 изменяющейся функции к ее среднему за по периода значению. Для синусоцдального тока

Иногда пользуются понятием коэффициента формы несин; вой функции, определенного слецукжщм образом;

ло модулю ~РДН по. модулю знзченне тока.

§ 3.4, Изображение синусоидально изм

-------.лхся величин векто-

рами па комплеюной плосшкти. Комплексная амплитуда. КомплсшЯ действующего значения. На рис. 3.2 дана комплексная Ююаахчь,! на которой можно изобразить комплексные числа. Комплетсное имеет дейстшггелыгую (вещественную) и мт1мую части. По оси i комплексной шюскосш откладывают действительную часть i ного числа, а по оси ординат - мнимую часть. На оси действ значений сгавпм +1, а на оси мнимых значеикй+i(i = l/=:T). Из курса математики известна формула Эйлера

e° = coscs + /sina.

Комплексное число е изображают на комплексной вектором, численно равным единице и сосгавляюпум угол t. вещественных значении (осью + I). Угол а отсчитываем против часо-J вой стрелки от оси 4- I. Модуль функции

I е ! = Vcost + siii = I.

не измеряют приборами элеитромагнитной, электрода н. Принцип действия иэиеригельных приборов различ I иьи систем изучают в курсе электрических нзмеренвй. f J- 1

* есниусоидальных периодичепснх токов *.2 ц *4i.U. Sra-I

откяоиение косвенно свидетельствует о том, насколько несинусовдаридшД тадт отличается от синусоцдального.

Проекция (функции е? на ось + I равна cos а, а на ось +/ равиа ыпа. Если вместо функции е ° взять функцию / е , то / е° = / cos а + IIщ sin а.

На комплексной плоскости эта функция, так же как и функция е/ , изобразится под углом а к оси + I, но величина вектора Судет в / раз больше.

Угол а в формуле (3.8) может быть любым. Положим, что а = = Л-ф, т. е. угол а изменяется прямо пропорционально времени. Тогда

/едсй+*) = cos (tot+Ч)) + у/ sin (at+if). (3.9)

Слагаемое / cos (<of + ф) представляет собой действительную часть (Re) выражения /, еУ* :

cos (of+Ф) = Re (3.10а)

а функция / sin(coi-J-iJi) есть коэффициент при мнимой частч (1ш) выражения / б<* +*>:

/=/ sin (wi +ij>) = / еЯ *). (3.106J

Таким образом, синусондалыю изменяющийся ток i [срг(3.1) и (3.106)] можно представить как 1т/Ч-+*>,

или, что то же самое, как проекцию вращающегося вектора /те<+** на ось -{- / (рис. 3.3).

Исторнческн сложилось так, что в рад1ютехк гче-ской литературе аа основу обычна гринимяюг не синусоиду, а косинусоиду и потому пользуются формулой (а.10а).

с целью единообразия принято на комплекс- рдс, з.З

ной плоскости изображать векторы синусоидально изменяющихся во времени велич1ш для момента времени ( = 0. При этом вектор / е +* равен

(3.11)

Где / -комплоосиая величина, модуль котсой равен / , а угол, под KOTOfMM вектор / провед 1 к оси -(-1 на компле1хисй плоскости,

равен начальной фазе ф.

Величину называют комплексной амплитудой тока i. Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени W = 0.

Рассмотрим два числовых примера на переход от мгновенного значения тока к комплексной амплитуде и от комплексной амплитуды к мгновенному значению.

Пример 27. Ток i = SsiD((al + 2(f)A. Записать выражение для Комплексной амплитуды этого тока.

, Решение. В данном случае / = 8 А, = 20°. Следовательно,

/ -8е;-А.

Пример 28. Комплексная амплитуда тока / = 25 е-зо Д. Запи- ь выражение для мптваиюго значения этого тока.