где А условно означает, что производится определенная операция над координатами точки М, даваемая системой уравнений (Ш. 1) и коротко записывающаяся с помощью матрицы (III. 2).

Преобразование произвольной функции координат f{x,y,z) при преобразовании координат (III. 1) может быть записано подобным же образом:

r(x,y,z)==Af(x,y,z) (III. За)

При этом соответствующее операции А преобразование (III. 1) производится над каждой координатой, вследствие чего меняется вся функция.

Символ А, указывающий на определенную операцию, которую нужно произвести над следующей за ним функцией, называют оператором. Следовательно, каждому преобразованию симметрии можно поставить в соответствие некоторую матрицу-оператор.

Если произвести над той же системой обратный поворот (т. е. поворот на угол -ф), то точка М снова возвращается в М, причем, как это легко показать на основе уравнений (III. 1), преобразование М(л:, i/, z) в M(x,y,z) имеет вид

л: = ж cos ф - у sin (р y = xsm(f + ycosq> (1П. 4)

2 = z

с матрицей преобразования

(cos ф - sin ф и N sin ф cos ф О 1 О 0 1/

(Ш.Б)

что можно коротко записать так:

М = АМ (III. 6)

Очевидно, что. последовательное применение операций Л и Л к точке М переводит ее самое в себя. Иными словами,

ААМ = М (III. 7)

и, следовательно, матрица ЛЛ соответствует тождественному преобразованию Е. Можно показать, что у такой матрицы все недиагональные элементы равны нулю, а диагональные - единице. Поэтому матрица называется единичной. Для трехмерного случая она имеет вид

,1 О Os

f о 1 oj

vo о 1/

(III. 8)

и соответствует преобразованию:

х = х

У = У г = г

Таким образом ЛЛ = £. В этом случае говорят, что матрицы Л и Л являются взаимно обратными. Поэтому, если некоторому

(III. 8а)

преобразованию соответствует матрица Л, то обратному преобразованию соответствует обратная матрица Л = Л .

Заметим, что обратная матрица Л , определяемая формулой (III. 5), может быть получена из исходной Л простой заменой столбцов на строки. Такая операция над матрицей называется транспонированием. Оказывается, что и в общем случае любой матрицы подобного рода * обратная ей будет просто транспонированной.

Операции отражений записываются совершенно аналогично операциям поворотов. Например, отражению в плоскости ху соответствует преобразование х = х, у = у и г = -z с матрицей

10 0>

(Ш.9)

=(:: о)

VO о -1/

,-1 О 0. 1 = 1 0-1 о 1 V о 0-1/

(III. 10)

а инверсия в начале координат имеет вид: х = -х, /-1 О

/ = -у. А-

В общем случае п координат Xi, Хч, Xz, .... Хп (?мepнoe пространство) их линейное преобразование, аналогичное преобразованиям (III. 1) или (III. 10) для трехмерного случая, удобнее записать коротко следующим образом:

(;=1, 2...., п)

(III. 11)

где flij -некоторые постоянные коэффициенты.

Соответствующая этому преобразованию матрица имеет вид:

0,2 022

а in

а 1 а 2

(III. 12)

Приведенные выше матрицы (111.2), (III.5), (III.8), (III.9) и (III. 10) являются частными случаями матриц преобразования (III. 12) для случая трех переменных.

Можно показать, что для рассматриваемых поворотов и отражений матричные элементы Otj удовлетворяют определенным соотношениям

4 =

(/=1, 2,..., п)

Вещественной и унитарной, см. ниже.

или, в более короткой записи

(III. 13)

где 6 - символ Кронекера,

( 1, kr

Линейные преобразования (III. 11), для которых выполняются условия (111. 13), называются унитарными. Унитарность преобразовании поворотов и отражений, матрицы которых приведены выше, легко проверяется простым вычислением. Преобразования симметрии для молекулы, следовательно, являются унитарными.

Проведем последовательно два преобразования системы:

(/=1, 2.....п)

(/=1, 2,..., п)

(III. 14)

Коротко это можно записать подобно (111.3)

М=АМ М = ВМ

(111.14а)

где А и В -матрица первого и второго преобразований.

Очевидно, что такое последовательное применение двух преобразований X в х и х в х может быть осуществлено и путем непосредственного преобразования л: в дг

(t = l, 2,..., п)

М =СМ

(III. 15) (111.15а)

где С - матрица этого преобразования.

Подстановка первого из уравнений (III. 14а) во второе позволяет получить:

М = ВМ = ВАМ

Сравнивая это соотношение с (III. 15), мы видим, что:

(III. 16)

Определенная таким образом матрица С называется произведением матриц В на А. Элементы этой матрицы можно найти, если подставить первое из уравнений (111.14) во второе:

1 п п п п

/=1 ;=1 л=1 й=1 /=1

(III. 156)

Сравнивая (1П. 156) с (III. 15), получаем:

(III. 17)

т. е. элементы матрицы произведения двух матриц равны суммам произведений элементов соответствующей строки множимого на элементы соответствующего столбца множителя. В связи с этим уместно подчеркнуть, что произведение матриц в общем случае не является коммутативным, т. е.

ВАфАВ

(III. 18)

Таким образом, последовательное применение двух преобразований к некоторой функции может быть описано одной матрицей, равной произведению матриц этих преобразований.

Как видим-, каждому преобразованию симметрии системы можно поставить в соответствие некоторую матрицу-оператор. При этом обратному преобразованию симметрии соответствует обратная матрица, последовательному применению двух операций симметрии - произведение соответствующих матриц, а тождественному преобразованию - единичная матрица. Таким образом, геометрические свойства симметрии оказываются полностью переведенными на язык матриц-операторов, который является существенным при использовании теории групп в квантовомеханических исследованиях.

111.2. ГРУППЫ ПРЕОБРАЗОВАНИЙ СИММЕТРИИ

Наиболее важным свойством преобразований симметрии для данной системы, является то, что они образуют группу в математическом смысле этого, слова. Под группой понимается некоторая совокупность элементов *, удовлетворяющих следующим четырем условиям: определена операция умножения двух элементов, причем произведение любых двух элементов из рассматриваемой совокупности есть элемент той же совокупности; умножению присущ закон ассоциативности, т. е. {АВ)С - А{ВС), где Л, В, С - элементы группы; среди элементов группы содержится единичный Е, т. е. такой элемент, который в произведении с любым другим не меняет его; для каждого элемента совокупности существует обратный Л , так что ЛЛ = Е.

Легко видеть, что совокупность преобразований симметрии для данной системы удовлетворяет всем вышеперечисленным условиям для группы. Действительно, произведение двух преобразований симметрии согласно вышеизложенному есть результат их последовательного применения, и так как каждое из них, по определению, совмещает систему с самой собой, то и их произведение совмещает

* Природа этих элементов совершенно не существенна.

ее с самой собой и, следовательно, есть преобразование симметрии. Далее, единичный элемент есть тождественное преобразование, а обратный элемент, как было показано выше, дается обратным преобразованием. Легко также проверить закон ассоциативности.

Но если совокупность преобразований симметрии для данной системы образует группу, то к этой совокупности можно сразу применить все результаты, полученные в математической теории групп. Мы приведем здесь лишь некоторые из них.

Количество элементов группы называется ее порядком. Легко видеть, что для молекул порядок группы - количество преобразований симметрии - может быть как конечным, так и бесконечным. Последний случай реализуется, например, для линейной молекулы, для которой поворот на любой угол вокруг оси молекулы есть преобразование симметрии. Если порядок группы не есть простое число, то из этой группы можно выделить подгруппы, т. е. меньшие совокупности элементов, образующих сами по себе группы.

Два элемента Л и В называются сопряженными между собой, если среди элементов группы существует такой третий элемент Р, для которого

А = РВР- (III. 19)

Можно легко показать, что если А сопряжено с В, а В с С, то А сопряжено с С. Это свойство позволяет разделить все элементы группы на совокупности сопряженных между собой элементов. Эти совокупности называются классами.

Существует простой геометрический способ, с помощью которого можно легко распределить элементы группы по классам. Пусть А есть поворот вокруг оси Оа на некоторый угол ф, а В - поворот на тот же угол вокруг оси ОЬ. Тогда, если среди элементов группы существует такой элемент Р, который переводит ось ОЬ в Оа, то Л = РВР- и, следовательно, Л и В принадлежат к одному и тому же классу. Доказательство этого утверждения получается непосредственно из геометрических соображений [29, с. 399]. Распределение элементов группы преобразований по классам является существенным для приложений.

Необходимо отметить, что преобразования симметрии для молекулы таковы, что по крайней мере одна ее точка остается неизменной при последовательном их применении. В противном случае, как легко видеть, они могли бы привести к поступательному перемещению молекулы, при котором она не совмещается сама с собой. Группы таких преобразований называются точечными. Только такие группы, следовательно, и интересуют нас здесь. Простейшими из них являются (рис. HI. 2): С (п = 1, 2, ..., п), содержащие одну ось п-го порядка и п элементов: С , С\, С1.....С =

==£; группы Cnh и Cnv (в том числе Ссх, ), получающиеся присоединением к оси п-го порядка плоскостей отражения оп и о ; группы Dih, являющиеся результатом присоединения к оси п-го порядка перпендикулярной ей оси 2-го порядка; группы тетраэдра Т, Та и

Тп; группы октаэдра О и и группы икосаэдра J;;-

этих групп, количества элементов симметрии и их распределение

по классам дано в общих руководствах (см. [29, гл. XIIJ).

и

Oh <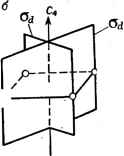

Рис. III. 2. Элементы симметрии некоторых точечных групп:

в-ось 4-го порядка, плоскости и ст группы С; б-плоскости группы Cfji в-ось 3-го порядка, плоскости группы Cj.

Разберем в качестве примера группу Он, соответствующую симметрии октаэдрического комплекса с одинаковыми лиган-дами, - группу всех преобразований куба (рис. 1П.З). К ней относятся: три оси 4-го порядка С4, проходящие через центры противоположных граней (в случае октаэдрического комплекса - соединяющие противоположные лиганды) и совпадающие с ними три оси 2-го порядка Сг = С; четыре оси 3-го порядка Сз, совпадающие с диагоналями куба; шесть осей 2-го порядка Сг, соединяющие середины противополож-. ных ребер; центр симметрии; три плоскости симметрии Oh, параллельные граням куба, и шесть плоскостей симметрии Od, проходящих через каждую пару противоположных ребер. Для определения количества элементов и их распределения по классам удобнее сначала выделить подгруппу О-совокупность всех поворотов - известную группу поворотов октаэдра.

Согласно приведенному выше геометрическому способу распределения элементов по классам вращения на одинаковый угол вокруг различных осей входят в один класс, если среди поворотов группы О имеются такие, которые переводят одну ось в другую. Пользуясь этим правилом, легко установить, что в группе О содержится 24 элемента, распределенные по пяти классам: класс Е, содержащий только тождественный элемент (тождественное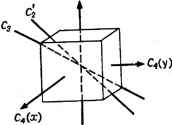

Рис. III. 3. Оси симметрии куба, и как самостоятельную