можно представить в виде простого произведения одноэлектронных функций *:

Ф (П, Г2.....г ) = (р, (г,) (Р2 (Tj) ... (р ( ) (II. 34)

Предположим, что функции fpi{r) ортонормированьг J (р* (О ф,. (О dx = bif (/, /= I, 2,... и)

т. е.:

(11.35)

Для нахождения их вида можно воспользоваться вариационным принципом [29, с. 81; 33, гл. VII], согласно которому искомые волновые функции из класса (11.34) должны удовлетворять условию минимума полной энергии системы, вычисленной с гамильтонианом Й уравнения Шредингера:

£ = ф*ЯФйт; 6£ = 6 ф*ЯФйт = 0 (11.36)

Подставив (II. 34) в (II. 36) и проварьировав по неизвестным

функциям 9i(ri), мы получим следующую систему уравнений, которым должны удовлетворять эти функции

h \г-г[

Ф (г) = 0 (ft=l, 2,..., п) (11.37)

(11.38)

где Й° - часть электронного гамильтониана, содержащая операторы кинетической энергии электрона Т и энергии его взаимодей-

ствия с ядрами UiRa - радиус-вектор ядра а):

Физический смысл интегрального члена в этом уравнении весьма прост: интеграл -7\~\fpi(r)f dx равен энергии электростатического отталкивания электрона от другого электронного

заряда, распределенного в пространстве с плотностью ефг(Г{)2.

Мы получили полное разделение координат электронов, ибо каждое из п уравнений системы (11.37) есть уравнение относительно функции переменных только одного электрона. Правда, эта система является сложной, интегродифференциальной. Ее решения

* По физическому смыслу волновой функции квадрат модуля ф. (г.) 2 представляет вероятность нахождения /-го электрона в точке г. Квадрат модуля функции (11.34), равный произведению квадратов модулей функций <Pj £),

имеет смысл вероятности нахождения 1-го электрона в точке Ti, 2-го - в и т. д. Ниже показано, что представление (II. 34) недостаточно точно.

** Отметим, что в методе Хартри ортогональности функции не требуется.

можно получить посредством некоторого Метода итераций, названного методом самосогласованного поля.

->

Примем некоторую систему функций щ{г) [полученную, например, при полном игнорировании взаимодействия между электронами, т. е. интегральных членов в системе (11.37)] за исходную и вычислим с ее помощью все члены вида

<р;() Р,(г)

(11.39)

означающие потенциал взаимодействия данного электрона со средним полем остальных. Подставив эти выражения в систему (11.37), мы получим уже независимые обыкновенные дифференциальные уравнения 2-го порядка вида:

(11.40)

Из решения этих уравнений (в общем случае они могут быть получены численными методами) мы получим новую систему

функции фй(г), которые более точны, чем исходные (и собственные значения бь). Зная эти функции можно вычислить более точные значения потенциалов Vk{r) по уравнению (11.39), что в свою очередь позволит получить еще более точную систему одноэлектронных функций фА и т. д. до тех пор, пока новое собственное значение еь и собственные функции фь практически не будут отличаться от предыдущих. Тогда полученное решение будет самосогласованным. Описанный метод расчета одноэлектронных функций был впервые предложен Хартри [31].

Однако представление полной электронной волновой функции в виде простого произведения одноэлектронных функций (11.34) не удовлетворяет принципу неразличимости частиц с полуцелым спином - функция (11.34) не является антисимметричной по отношению к перестановке координат двух электронов. Как было показано Фоком для системы с замкнутой оболочкой такому свойству удовлетворяет однодетерминантное представление (И. 17). Подстановка функции (П.17) в условие (П.36) и варьирование по всем одноэлектронным функциям приводит к значительно более

сложной системе уравнений для их координатных частей щ(г), чем (11.40) (уравнения Хартри - Фока [32]):

Йо + 2

п/2 , ->

ф(г0ф,-(О

dx-B

ФЛГ)-

=1 L

(р.(г) = 0 (ft = 1, 2,..., п/2) (11.41)

Здесь принято во внимание, что в соответствии с предположением о замкнутости электронной оболочки полное число электронов п четно, и в каждом координатном состоянии ф,- имеется по два электрона с противоположными спинами. При этом вторая сумма в (П. 41)-обменная поправка - содержит только п/2 членов, так как она отлична от нуля только для взаимодействия между электронами с параллельными спинами (член с i = k, соответствующий фиктивному взаимодействию k-то электрона с самим собой, автоматически исключается, поскольку он входит в две суммы с противоположными знаками).

Константы Егй появляются как множители Лагранжа при дополнительных условиях ортогональности и нормировки функций Фй и фг (11.35). От большей части этих констант можно избавиться, если от функций ф4 перейти к их линейным комбинациям Ф,- или, как говорят, произвести над базисом функций ф унитарное преобразование [см. формулы (П1.13) на стр. 52]. Такое преобразование не меняет исходной детерминатной функции (П.17), варьированием которой были получены уравнения Хартри - Фока, и, следовательно, энергии системы [21, Приложение 8], но коэффициенты преобразования можно выбрать так, что новые недиагональные константы будут равны нулю. Вводя обозначения

kk = -fe и ik ~ оператор перестановки индексов inky стоящей за ним функции, имеем (для простоты штрих у преобразованных функций ф опущен):

ti \r-r\

{k = l, 2.....п/2)

В этом случае Ей имеет смысл одноэлектронной энергии в самосогласованном состоянии фй и уравнения. (11.42) могут быть записаны в форме уравнений Шредингера

Pft(r) = £fc(p;(T)

(II. 42)

\ (О = (г) (ft = 1, 2.....п/2)

h J к-ГI

(11.43)

(II. 44)

- одноэлектронный фоковский эффективный гамильтониан.

Умножив уравнение (11.42) или (11.43) слева на ф(г) и проинтегрировав по г, легко находим, что

п/2 п/2

Ek=Hik-Y,imm-mki\)=Hi+y[2i{i, к)-к{1,щ (11.45)

где двухэлектронные кулоновские \ii\kk\ = 1 {и/г) и обменные [ik\ki] = K{i,k) интегралы даются формулами (11.22), (И-23). Отсюда видно, что с учетом выражения (П. 38). для Йо, энергия

электрона в k-u одноэлектроииом состоянии равна сумме кинетической энергии его, энергии взаимодействия с ядром гии его кулоновского и обменного взаимодействия со всеми ными электронами. Совокупность всех одноэлектронных мы получим, просуммировав выражение (11.45) по всем k п/2 и умножив его на 2 (соответственно числу электронов дом состоянии k):

п/2 п/2 п/2 п/2

2E£ft = 2K + 2E J: [21(1. к)-Ки. k)] fc=i k=i fc=i =i

средней и экер-осталь-энергий от 1 до в каж-

(11.46)

Заметим, что в этом выражении взаимодействие между электронами учитывается дважды: один раз при суммировании по i и другой -по /г. Поэтому полная энергия системы Е, равная сумме кинетических энергий электронов, их энергий взаимодействия с ядром и между собой, отлична от суммы одноэлектронных энергий на величину энергии взаимодействия между электронами:

п/2 п/2

£ = 2£fe- Е [2/(/,*)-/((;, ft)] =-I, ft= i

пП n/2

(П. 47)

ГЛАВА

ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП

В теории электронного строения и свойств координационных соединений большое (иногда фундаментальное) значение имеют представления о симметрии, наиболее полное описание которых достигается применением математической теории групп, занимающей, поэтому, важное место в квантовой химии.

ПРЕОБРАЗОВАНИЕ СИММЕТРИИ. МАТРИЦЫ ПРЕОБРАЗОВАНИЙ

Возможность использования теории групп в квантовомехани-ческих исследованиях основывается на свойствах симметрии изучаемых атомных систем. Покажем, каким образом геометрические, свойства симметрии молекулы могут быть переведены на абстрактный, но удобный математический язык. Если при некотором перемещении (повороте, отражении) молекулы она совмещается сама с собой, то такое перемещение называется преобразованием или операцией симметрии. Например, в плоской треугольной молекуле Уз (рис. III. 1) преобразованиями симметрии являются повороты: вокруг оси Cz (перпендикулярной к плоскости молекулы) на углы 2я/3, 4я/3, 2я и вокруг осей А]Ви Л2В2, зз на углы л, 2я, а также отражения в плоскостях, проходящих через эти оси и перпендикулярных плоскости молекулы.

Легко видеть, что простейшими операциями симметрии для молекул могут быть только повороты и отражения (для неограниченной среды - кристалла - к ним ещ§ добавляются переносы). Операцию симметрии, соответствующую повороту вокруг некоторой оси на угол 2я/п, обозначим посредством С . Очевидно, что если тело совмещается само с собой, при повороте на некоторый угол, то оно будет вести себя подобным же образом при повторении этого поворота любое целое число раз.

Результат последовательного применения двух операций симметрии назовем их произведением. Следовательно, если С - операция симметрии тела, то и C C = Сп есть тоже операция симметрии; в общем случае Ср (где р -целое число) тоже является операцией симметрии тела. В частности, Сп соответствует повороту на угол 2я, т. е. не меняет положения тела в простран-

Подробнее см. [60-67; 29, гл. 12].

стве; такая операция называется тождественным преобразованием и обозначается посредством Е:Сп = Е- Ось вращения при операции Сп называется осью п-го порядка.

Операция симметрии а обозначает отражение в плоскости. Очевидно, что а ~ Е. При наличии некоторой оси симметрии операция отражения в плоскости, проходящей через эту ось, обозначается через Ov и Od, а отражение в плоскости, перп.эндикулярной этой оси, через оп- Последовательное применение операций С и а называется зеркальноповоротным преобразованием: S = С с . В частности, поворот на угол я с последующим отражением в плоскости, перпендикулярной к оси поворота, называется инверсией / в точке пересечения этой оси с плоскостью: / = S2 = = COh- Из этих простейших операций симметрии могут быть составлены все известные симметричные преобразования молекул.

Термин преобразование для этих перемещений (поворотов и отражений) молекулы происходит от того, что математическим выражением такого

перемещения является простое линейное преобразование координатных осей от одной системы к другой. Так, поворот молекулы на угол ф вокруг оси Oz равносилен такому преобразованию координатной системы, при котором любая точка М (х, у, z) переходит в точку M{x,y,z), причем:

ж = ж COS ф -- J/ sin ф

J/ = - ж sin ф -f 2/ cos ф

2 = г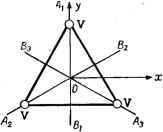

Рис.

III. 1. Элементы симметрии треугольника.

(III. 1)

В дальнейшем линейное преобразование типа (III. 1) встречается часто, поэтому удобно иметь длянего краткую запись. Запишем его в более симметричной форме

х - COS ф.ж-{-51пф.г/+0.2

= sin ф X -Н cos ф г/ -f О 2 (III. 1а)

г = 0-х + 0-у + 1- г

и составим квадратную таблицу из коэффициентов при координатах х, у, z:

f С08ф з1Пф On

- sin ф cos ф О j \ О 0 1/

(III.2)

Эта таблица носит название матрицы преобразования (111. 1). С помощью матрицы А преобразование точки M.(x,y,z) в точку W [х!,у,z) коротко запишется так

и = АМ (III. 3)