динамики 6 кристалле при комнатной температуре можно отме* тить всегда, когда окружение комплекса имеет кубическую симметрию и взаимодействие между комплексами мало (в этих случаях фазовый переход со стабилизацией искажений на каждом центре в принципе может произойти при более низкой температуре).

Не исключена, однако, ситуация, когда условия в кристалле стабилизируют не одну, а несколько близких по энергии конфигураций координационной сферы, различающихся пространственным строением последней. В этом случае такие конфигурации могут проявиться кристаллохимически в виде сосуществующих кристаллических изомеров.

Весьма интересный пример этого типа представляют собой так называемые дисторсионные изомеры двухвалентной меди, впервые полученные и исследованные Гажо с сотрудниками (см. обзор [434]). Эти изомеры различаются тем, что при одинаковых составе и лигандном окружении меди расстояния медь -лиганд отличны в разных изомерах. При этом они различаются не только По способу синтеза, но и по внешнему виду, форме кристаллов, химическому поведению, растворимости, спектроскопическим свойствам и др. Кроме того, возможны переход одного изомера в другой под влиянием давления, температуры или времени хранения. В некоторых случаях получены не только два основных изомера (названные а и Р), но и группа так называемых промежуточных препаратов.

Первое и более простое вещество, для которого получены дисторсионные изомеры, это Си(КНз)2Х2, где X - С1, Вг. Сразу же после их синтеза М. Е. Дяткина и М. А. Порай-Кошиц [435] выдвинули предположение, что существование их обусловлено несколькими возможными типами искажения координационной сферы меди, возникающими из-за эффекта Яна - Теллера. Однако в работе [435] не было учтено, что различия в лигандах первой координационной сферы, строго говоря, снимают вырождение и, следовательно, ожидаемые искажения не могут быть собственно ян-теллеровского типа [436]. Лир [278] отметил по этому поводу, что в случаях, подобных рассматриваемому, в принципе возможны искажения псевдо-ян-теллеровского типа.

В основном правильный - в идейном плане - подход к задаче не смог в то время привести к сколь-нибудь удовлетворительному ее решению из-за недостаточной разработанности теории вибронных взаимодействий в электронно-вырожденных состояниях, включающей в себя эффект Яна - Теллера и псевдоэффект Яна - Тел-, лера как частные случаи.

Из полученных выше результатов объяснение происхождения дисторсионных изомеров получается как закономерное следствие из теории, учитывающей электронные (точнее, вибронные) свойства ц. а. Си(П) в сочетании со стабилизирующим влиянием кристалла в целом. Покажем это на примере упомянутыс соединений

си(ынз)2Х2. ;

Примем во внимание, что кристалл состоит из параллельных цепей, каждая из которых имеет мотив, иллюстрированный на рйс. Vni. 4, а, в котором все атомы X занимают эквивалентные мос-тиковые положения [437]. Внутри цепи взаимодействие между медными центрами через мостиковые атомы сильное, в то время, как цепи связаны между собой слабыми ван-дер-ваальсовыми (или водородными) связями. Каждый атом меди окружен четырьмя атомами X в плоскости квадрата и двумя атомами А в по-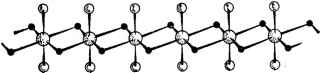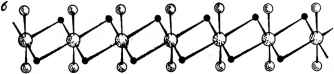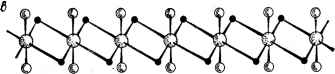

Рис. VII 1.4. Неискаженная структура цепи СиАгХг (а) и две ее искаженные конфигурации (б и в), соответствующие двум эквивалентным минимумам адиабатического потенциала на каждом центре (псевдоэффекту Япа - Теллера) и кооперативным явлениям в цепи.

ложениях 1 и 4. Ввиду различий между атомами А и X вырождение основного состояния Си(П) в октаэдре снимается, Eg-repM расщепляется на Mig и Big. Обозначим это расщепление через 2Д. Для простоты предположим, что терм Aig ниже (приведенные рассуждения остаются теми же и в противоположном случае).

Если предположить, что атомы X в плоскости образуют правильный квадрат, то полиэдр CUX4A2 является тетрагонально искаженным октаэдром симметрии Dth. Рассмотрим псевдоэффект Яна - Теллера на орбитальных состояниях Aig и Big такого комплекса (раздел VI. 3). Замечая, что этот случай полностью соответствует рассмотренному на стр. 219, можно сразу воспользоваться полученными там результатами. В частности нормальная координата Q, перемешивающая состояния A\g и Big, преобразуется по симметрии Big (так как Aig X Big = Big) и соответствующие ему смещения ядер в группе совпадают со смещениями

Q2 в группе Q; приведенными на рис. VI. 1.. Константа связи с этими колебаниями по (VI. 56) дается выражением

(VIII. 9)

где -ф и ijiBig- волновые функции смешиваемых псевдовырожденных состояний и B,g, которые в предельном случае теории кристаллического поля совпадают с функциями Srfz и 3dx~y- [для с?-дырки в конфигурации Cu2+(3d)]. Для адиабатических потенциалов получаются выражения (VI. 58)

= yKQ ± л/А + aQ

(VIII. 10)

где К == Мсо, ш - частота соответствующих b,g- колебаний (М - приведенная масса), иллюстрируемых на рис. VI. И (стр. 220). Далее предположим, что выполняется условие (VI. 59) Д < а/К, т. е. нижний лист потенциала для основного состояния имеет два минимума (рис. VI. 11,6) при значениях. ±Qo, определяемых формулой (VI. 60).

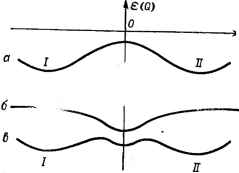Рис. VIII. 5. Адиабатический потенциал как функция координаты Q, соответствующей искажению, показанному на рис. VIII. 4, б:

с-для отдельной кепи CuAjXj; б-для межмоте-Куляр,.о.о взаимодействия цпей; в-с:Тар ый для кристалла в целом.

формулой (VI. 60).

Таким образом, на каждом центре вибронное взаимодействие (псевдоэффект Яна - Теллера) приводит к искажению тетрагональной бипирамиды, так что квадрат основания с атомами X в вершинах превращается в ромб с большой диагональю вдоль оси Ох (минимум / на рис. VIII. 5, а) или вдоль оси Оу (минимум ).

Ввиду сильного взаимодействия между искажениями на соседних центрах в цепи (из-за общих атомов X), последняя легко переходит в состояние упорядочения, в котором искажения скорре-лированы, и остается упорядоченной вплоть до высоких температур. Здесь вибронные искажения фиксируются вторым из указанных выше факторов - фазовым переходом. С учетом этого можем предположить, что при комнатной температуре отдельная цепь имеет два устойчивых состояния / и (рис. VIII.4, б, в), соответствующих двум минимумам для каждого центра (/ и на рис. VIII. 5, а). Мы пришли, следовательно, к выводу о возможности двух эквивалентных структур цепи СиХгАг, обязанных псевдоэффекту Яна - Теллера на каждом бипирамидальном центре CUX4A2 и упорядочению искажений в ней из-за сильного взаимодействия между центрами.

Остается исследовать еще один важный кристаллический фактор - взаимодействие между цепями. Анализ структуры кристалла из параллельных цепей показывает, что взаимодействие между цепями оптимально при неискаженной структуре каждой цепи, когда кристалл в целом получается кубическим. Действительно, в таком кристалле соответствующие расстояния между атомами минимальны и увеличиваются при искажении цепей до структуры / или . Разность энергий взаимодействий между цепями в кубическом кристалле и в кристаллах с цепями типа / или в принципе могла бы быть оценена полуэмпирически.

В отсутствие такого расчета для качественного анализа ситуации можно предположить, что энергия взаимодействия цепей в кристалле имеет минимум при Q = 0 (рис. VIII. 5, б), где Q - координата искажения цепей, соответствующая приведенной выше координате типа Big для каждого центра. Складывая адиабатическую энергию цепи (рис. VIII. 5, о) с энергией взаимодействия цепей как функцию Q (рис. VIII.5,б), мы получим результирующую полную энергию кристалла (рис. VIII. 5, е), которая в принятых предположениях имеет три минимума: к двум минимумам / и для энергии цепей, соответствующим искаженным конфигурациям, добавляется неглубокий минимум для неискаженной кубической конфигурации при Q = 0.

Дополнительные минимумы мы получим в этой схеме для кристалла, в котором часть цепей находится в минимуме /, а часть - в минимуме . Для них взаимодействия между цепями (по тем же соображениям, что и приведенные выше) еще меньше, чем когда они все скоррелированы (упорядочены) между собой и находятся в одном типе минимумов (или /, или ). Поэтому-то дополнительные минимумы менее глубоки, чем минимумы I н II для полностью упорядоченных кристаллов (но более глубоки, чем минимум для кубического кристалла при Q = 0; предполагается, что вибронная энергия внутри цепей превалирует над межмолекулярной).

Легко показать, что приведенная картина качественно объясняет все основные факты, наблюдаемые в дисторсионной изомерии соединений CUX2A2. Действительно, состояния наиболее глубоких минимумов (/ или ) соответствуют наблюдаемым а-изомерам с соответствующей структурой, приведенной на pncVIII, 4, б, е. Относительному минимуму при Q = О соответствует неустойчивый р-изомер, имеющий кубическую структуру с правильной бипира-мидой на каждом центре, а дополнительным относительным минимумам с нескоррелированными между цепями искажениями соответствуют описанные выше наблюдаемые промежуточные препараты. Такая интерпретация находится в согласии со всеми упомянутыми выше особенностями этих изомеров: с поведением под влиянием температуры и давления; с методами приготовления; со спектроскопическими свойствами; с условиями перехода одного в другой и др. (см. [434]).

Специально необходимо отметить, что хорошие кристаллы получаются только в случае р-изомера, т. е. тогда, когда, согласно теории, межмолекулярное взаимодействие, способствующее образованию кристалла, максимально. Напротив, а-изомер и промежуточные препараты, в согласии с отмеченным выше слабым взаимодействием между цепями в них, не получаются в виде таких кристаллов. В этом отношении существенным может оказаться и тот факт, что именно в случае р-изомера (и только в этом случае) кристалл Си(ЫНз)2Х2 содержит большую долю примеси соедине- ния NH4X [438]. Последнее само по себе кристаллизуется в кубический кристалл, изоморфный наблюдаемому р-изомеру, так что эти два соединения легко образуют смешанные кубические кристаллы. Вполне возможно, что кубическая структура цепей Си(ЫНз)2Х2, неустойчивая сама по себе из-за псевдоэффекта Яна-Теллера на каждом центре, поддерживается не только (или не столько) описанными выше межмолекулярными взаимодействиями между цепями, а наличием большого числа примесных молекул NH4X, чередующихся в цепи с молекулами Си(ННз)гХ2 (о пропорции ~ 1:1). Теоретически решить вопрос о том, что является основной причиной стабилизации кубической структуры кристалла - при- меси в цепях или взаимодействие между цепями - можно будет только, если удастся оценить энергию последнего как функцию искажений цепей.

Другой нерешенной в теоретическом плане задачей, но весьма актуальной в аспекте обсуждаемой проблемы, остается проверка выполнения критерия псевдоэффекта Яна - Теллера (VI. 59) в рассматриваемых соединениях Си(ЫНз)2С12 и Си(ЫНз)2Вг2.

Представляется, что в какой-то мере аналогично, по крайней мере на таких же принципиальных основах, можно качественно объяснить происхождение и других изомеров Си (II). В частности, ближе всего к изложенной схеме рассуждений подходят изомеры Cu(NH3)2(NCS)2 [439].

Описанный здесь метод исследования происхождения кристал- . лических структур на основе электронных и вибронных свойств образующих кристалл компонент на примере изомеров двухвалентной меди в действительности имеет более общее значение.и может быть использован для рассмотрения широкого класса соединений. К последним относятся, в частности, различные цепочечные образования металлоорганической природы и другие квазиодномерные структуры (см., например, [440]).

ГЛАВА IX

ТЕПЛОТЫ ОБРАЗОВАНИЯ, РЕАКЦИОННАЯ СПОСОБНОСТЬ, МЕХАНИЗМЫ РЕАКЦИЙ

Проблема реакционной способности и механизмов реакции - сердцевина химической науки - в последние годы получила дальнейшее развитие на основе более глубокого исследования электронного строения молекулярных систем.

JX.1. ЭЛЕКТРОННЫЕ ФАКТОРЫ В ТЕПЛОТАХ ОБРАЗОВАНИЯ

Теплоты образования ДЯ, или устойчивость, можно определить как величину разности энергии координационной системы в целом и ее составных частей (центрального атома и лигандов) в свободном (газообразном) состоянии. Практическое определение ДЯ довольно сложно [441, 442]. В большинстве случаев реакции комплексообразования протекают в растворах, чаще всего водных, в которых исходные и конечные продукты гидратированы.

Рассмотрим теоретические возможности определения устойчивости комплексов. Согласно наиболее общей трактовке теории МО (теория поля лигандов) образование устойчивого комплекса связано с понижением энергии на связывающих МО по сравнению с энергией свободных ц. а. и лигандов (раздел V. 3). Чем ниже энергия связывающих МО и чем больше на них электронОЬ, тем устойчивее должен быть соответствующий комплекс. Но наряду со связывающими МО существуют и разрыхляющие, а также несвязы-вающие. Заполнение электронами разрыхляющих МО уменьшает устойчивость системы. Роль несвязывающих МО также существенна: хотя они и не образуют МО с лигандами, все же подвержены электростатическому влиянию последних. Можно, следовательно, утверждать, что устойчивость комплекса определяется:

распределением электронов по связывающим, несвязывающим а разрыхляющим МО, т. е. электронной конфигурацией;

энергией связи на каждой МО, т. е. величиной понижения энергии стабилизации на связывающей (или повышения энергии дестабилизации на разрыхляющей) МО по сравнению с энергией свободных частей. Эта энергия часто может быть приближенно охарактеризована с помощью параметра расщепления Д - разности энергии электрона в состояниях е и /2 в комплексе с кубической Симметрией;

взаимодействием (отталкиванием) атомных остовов, включающих ядра и внутренние (не учтенные в расчетах по методу МО