Стереохимия, как и симметрия, тесно связана со всеми физическими и химическими свойствами системы и может быть установлена по этим свойствам. Наиболее прямой путь такого процесса, как уже указывалось - непосредственное определение относительных координат атомов дифракционными методами. Но последними чаще всего изучают кристаллическое состояние. Для большинства координационных систем твердое состояние есть и наиболее устойчивое. Отсюда вытекает особое значение стереохимии координационных систем, находящихся в кристаллическом состоянии (кристаллохимии).

В кристаллохимии следует различать локальный и коллективный аспекты. Первый заключается в выявлении стереохимии отдельных структурных элементов кристалла, в то время как коллективный аспект учитывает их взаимодействие между собой и упаковку в кристалле. Оба аспекта одинаково важны в объяснении происхождения кристаллической структуры и ее свойств, хотя в литературе по кристаллохимии до сих пор обычно отдается предпочтение коллективному (кристаллическому) аспекту. Больше всего электронное строение влияет на кристаллохимию через ее локальный аспект, и примером этого служит рассмотренная выше зависимость координации от электронных свойств ц. а. и лигандов. В следующем разделе это утверждение иллюстрируется также на примере анализа происхождения изомеров двухвалентной меди.

Обширный материал по кристаллохимии координационных соединений собран и систематизирован М. А. Порай-Кошицем с сотрудниками, ими же проведена большая часть работ по рентгено-структурному анализу этих соединений [401, 404-406] (см. также [407-409]). Обобщением части из них является табл. VIII. 1 [401]. Широкое распространение получили так называемые я-комплек-сы - новый класс кристаллохимических систем [408].

Vm.2. ЭФФЕКТ ЯНА-ТЕЛЛЕРА В СТЕРЕОХИМИИ И КРИСТАЛЛОХИМИИ

Полуклассическое приближение. Правило относительности к средствам наблюдения

Как уже отмечалось в разделе VI. 2, в отсутствие электронного вырождения адиабатический потенциал системы, определяемый из решения электронного уравнения адиабатического приближения (VI. 3), имеет смысл потенциальной энергии ядер в поле электронов. Если этот потенциал имеет один абсолютный минимум (только в этом случае, вообще говоря, применимо адиабатическое приближение), то в хорошем приближении иногда можно рассматривать движения ядер как классическое движение частиц вдоль потенциальной поверхности - полуклассическое приближение. Именно оно было успешно использовано нми в главе VII при определении формы полос поглощения света; его плодотворно применяют к решению и других задач (в частности, в расчетах скоростей адиабатических реакций [411, гл. I и III]).

При наличии электронного вырождения (или псевдовырождения) вместо одной поверхности адиабатического потенциала появляется несколько (по кратности вырождения) поверхностей, пересекающихся в одной точке (точка вырождения). По этой причине каждая из них и все они вместе теряют простой физический смысл, становясь формальным понятием, особенно в районе пересечения (раздел VI. 2) [371]. В последнем задача превращается в сугубо квантовую, исключающую возможность использования полуклассического приближения. В этом случае поведение системы можно определить лишь после точного решения системы вибронных уравнений (раздел VI. 4).

Однако анализ вида адиабатического потенциала в различных электронно-вырожденных и псевдовырожденных случаях, рассмотренных в разделе VI.3 (f)HC. VI.5-VI.7), показывает, что при достаточно сильной вибронной связи - глубоких минимумах адиабатического потенциала - в области вблизи минимума вдали от точки пересечения поверхностей расстояние до следующей ветви поверхности становится достаточно большим (например, в случае -терма оно равно 4£ят)- В этой области, следовательно, можно снова вернуться к использованию полуклассического приближения.

Поступая подобным образом, нужно соблюдать известную осторожность и все время иметь в виду те квантовые эффекты, которые могут быть утеряны в таком полуклассическом рассмотрении. В настоящем разделе мы рассмотрим свойства стереохимии и кристаллохимии координационных систем, которые вытекают из такого качественного полуклассического исследования, с учетом тех очевидных квантовых эффектов, которые можно получить без подробного решения вибронных уравнений главы VI.

Обратимся сначала к свободным ян-теллеровским (или псевдо-ян-теллеровским) системам и выясним те условия, при которых ян-теллеровские искажения могут быть обнаружены экспериментально в стереохимии. Как было показано в разделе VI.3, системы с электронным вырождением или псевдовырождением обладают несколькими эквивалентными минимума адиабатического потенциала, соответствующими искаженным (по разным эквивалентным направлениям) пространственным конфигурациям ядер. Последние взаимно дополняют друг друга так, что в совокупности они не понижают исходную симметрию системы, для которой получается электронное вырождение. Поэтому в стационарном состоянии среднее искажение ядер, как уже отмечалось в главе VI, равно нулю.

В действительности, однако, система чаще всего оказывается с самого начала (в результате химической реакции, столкновения и др.) в искаженной квазистационарной конфигурации одного минимума. Тогда в зависимости от высоты барьера между минимумами она через некоторое время перейдет в состояние другого минимума и т. д. [29, с. 168].

При достаточно больших барьерах между минимумами адиабатического потенциала систему можно рассматривать как совершающую своеобразные заторможенные движения, связанные с

переходами между конфигурациями минимумом (стр. 227). Предположим, что искаженную конфигурацию ядер, соответствующую одному из минимумов адиабатического потенциала, можно охарактеризовать некоторым временем жизни т, после которого она, преодолевая барьер, переходит в эквивалентную конфигурацию другого (соседнего) минимума (т обратно пропорционально инверсионному расщеплению 6). Тогда в процессах взаимодействия системы с внещ-ним возмущением (в процессе измерения), характеризуемого некоторым временем т (время акта взаимодействия), возможно два предельных случая. Если

т<т (VIII. 2)

в измерении проявится только одна искаженная конфигурация, ибо за время измерения система не успевает перейти из одной конфигурации в другую. В этом случае в экспериментах система покажется соответствующей искаженной конфигурации. В другом предельном случае, когда

т>т

(VIII. 3)

за время измерения система успевает неоднократно переходить из одних конфигураций в другие (дополняющие первую до максимальной симметрии, рис. VI. 6), так что в опытных данных про* явится некоторая усредненная картина.

Отсюда следует, что выводы о симметрии системы, сделанные на основе экспериментальных данных, будут зависеть от метода измерения. В частности, в опытах по электронному поглощению (частота света велика, т мало) может наблюдаться расщепление электронных полос, соответствующее искаженной конфигурации системы, в то время как в спектре ЭПР (частота меньше, х больше) соответствующая линия окажется изотропной, соответствующей максимально-симметричной системе. Мы приходим, следовательно, к правилу относительности к средствам наблюдения: в свободной ян-теллеровской системе наблюдаемые ядерные конфигурации зависят от средств наблюдения и могут меняться от метода к методу [412, 413, 284].

Более того, так как инверсионное (туннельное) расщепление растет (а следовательно, т убывает) с температурой (стр. 240), то для одного и того же метода измерения (при том же т) может оказаться, что при низких температурах выполняется условие (VIII.2), т.е. в опыте будет наблюдаться искаженная конфигурация (низкая симметрия). При достаточно же высокой температуре т убывает настолько, что реализуется условие (VIII. 3) и в опыте проявляется усредненная полносимметричная картина. Именно таков наблюдаемый экспериментально и получивший затем объяснение температурный переход в спектре ЭПР ряда комплексов Си(II) [329].

Ниже рассматривается другой иллюстрирующий это правило пример, связанный с дипольной неустойчивостью молекул.

Дипольная неустойчивость и дипольный момент

Специальный случай стереохимии молекулярных систем с электронным вырождением или псевдовырождением представляют так называемые дипольно-неустойчивые системы, т. е. такие, для которых искажение, связанное с переходом из максимально-симметричного состояния в минимумы адиабатического потенциала, сопровождается образованием дипольного момента (раздел VI. 3) [291-294, 414]. Это возможно при наличии центра инверсии в случае псевдовырождения между двумя электронными состояниями противоположной четности или в случае 7 - 2-задачи для систем без центра инверсии. Напомним, что в системах с центром инверсии обычный эффект Яна - Теллера на вырожденных термах не может привести к дипольной неустойчивости.

Проявления дипольной неустойчивости весьма существенны во-первых, тогда, когда системы, которые традиционно считают симметричными й необладающими дипольным моментом, могут проявить свойства, присущие системам с дипольным

моментом, и, во-вторых, когда системы с собственным дипольным моментом, обычно предполагаемые твердодипольными, могут иметь две (или несколько) равновесные конфигурации, появившиеся в результате псевдовырождения и отличающиеся направлением дипольного момента, переходы между которыми существенно меняют проявляемые свойства.

Типичным примером второго варианта может служить молекула аммиака. Ее две равновесные конфигурации с противоположно направленными дипольными моментами вместе с инверсионным рас-, щеплением 6, обязанным туннелированию между этими двумя конфигурациями, показаны на рис. VIII. 2. При помещении совокупности таких молекул в электрическое поле их ориентационная поляризуемость оказывается иной, чем для твердодипольных молекул.

Расчет показывает [294], что с учетом больцмановского распределения и неравенств С б и pS С кТ, {ро - абсолютное значение дипольного момента в равновесной конфигурации), средний дипольный момент в полуклассическом приближении оказывается равным: *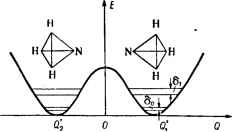

Рис. VIII. 2. Два минимума адиабатического потенциала для молекулы аммиака и инверсионное расщепление.

(VIII. 4)

[414].

* Это результат практически не зависит от учета квантования вращения

Аналогичная формула для системы с четырьмя дипольными минимумами адиабатического потенциала имеет вид [414]:

exp(-6/kT) + (kTJ6)sh({>/kT)

ЗкТ exp{-6/kT) + ch{6/kT)

(VII 1.5)

Выражения (VIII. 4) и (VIII. 5) существенно отличаются от получаемых в случае ориентационной поляризации твердых диполей

(VIII. 6)

как по абсолютной величине, так и-по температурной зависимости и совпадают с ним только в предельном случае 6<kT (рис. VIII. 3). В другом предельном случае (б кТ) выражение для р по (VIII. 4) перестает зависеть от температуры, совпадая со значением р - аЖ, характерным для симметричных молекул, не имеющих собственного дипольного момента.

Отсюда следует принципиальный вывод, что с учетом диполь-ной неустойчивости деление молекул на твердодипольные и симметричные по их поведению в электрическом поле (по температурной зависимости поляризации) условно: оба типа поведения - линейная зависимость поляризуемости от 1/Г и ее независимость от Т - присущи одним и тем же молекулам в различных областях температур (рис. VIII. 3). Последние же определяются величиной дипольной неустойчивости (ср. с обсуждаемым выше правилом относительности к средствам наблюдения). В частности, могут реализоваться и чисто предельные случаи, когда дипольная неустойчивость вообще отсутствует или когда барьеры между дипольными конфигурациями бесконечно велики (к последнему случаю относятся, например, двухатомные молекулы с различными атомами).

В практическом плане формула (VIII.4) предсказывает необходимость соблюдения особой осторожности при определении собственного дипольного момента ро по температурной зависимости поляризуемости. Из рис. VIII. 3 видно, что различия между р п р особенно существенны в области кТ 6. В частности, уже при кТ =ib р Up, и определение ро по формуле (VIII.5) приведет к занижению результата в 1,3 раза по сравнению с истинным значением, получаемым по формуле (VIII. 4) (см. в [415] справки по дипольным моментам и в [416] методы определения и обсуждение).

При слабой дипольной неустойчивости, когда 6у]кТ, как указывалось, электрические свойства системы приближаются к ожидаемым для симметричных молекул, не имеющих собственного дипольного момента. Если при этом 6 не очень велико, то с повышением температуры начнет проявляться температурная зависимость поляризуемости, интерпретируемая как появление (и возрастание) собственного дипольного мо.мента. Обнаружение этого эффекта представляется одной из интересных экспериментальных задач. Можно предположить, что этим эффектом объясняются наблюдае-

мые аномалии и температурная зависимость поляризации CCI4 [417], перилена [418] и др.

Дипольная неустойчивость может проявляться и в некоторых других свойствах молекулярных систем, таких, как: деполяризация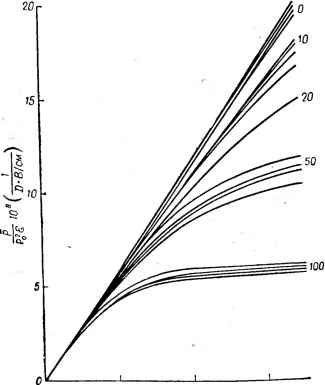

1 2 3

Рис. VIII. 3. Средние поляризуемости (в условных единицах) дй-польно-неустойчивых симметричных систем как функция температуры и величины туннельного расщепления 6 (подробности см. в работе [414]).

релеевского рассеяния света (см. [419]); возрастание диэлектрических потерь в микроволновой области; отклонение от центрального характера межмолекулярных сил; появление аномалий в колебательных и вращательных частотах и др. В частности, показано [420], что при наличии дипольной неустойчивости симметричные молекулы обладают характерным вращательным спектром поглощения, которого не может быть без учета дипольных искажений.

Влияние дипольной неустойчивости на спонтанную поляризацию кристаллов и сегнетоэлектрическне фазовые переходы см. ниже (стр. 292),