как симметрия. Симметрия многоатомной системы может быть определена - в самом общем виде - как совокупность операций поворотов и отражений, которые оставляют ее неизменной (см. раздел III. 1). По указанному определению симметрия может быть одной и той же для соверщенно разных по составу (и характеру связей) систем. Такой абстрактный характер этого понятия позволяет использовать для изучения симметрии и ее связи со свойствами системы очень эффективный математический аппарат - теорию групп (глава III). При этом можно получить некоторые общие, но точные сведения о строении и свойствах системы, которые тем эффективнее, чем выше симметрия. Координационные соединения обладают, вообще говоря, наиболее высокой симметрией среди всех типов молекул (раздел 1.2).

Симметрия отражается на всех без исключения свойствах системы и поэтому в принципе может быть определена экспериментально из любого типа измерений над системой. Практически, однако, такое определение эффективно только в том случае, если связь измеряемого свойства с симметрией непосредственна и хорошо изучена. Наиболее прямой путь экспериментального определения симметрии системы - это определение координат атомов по данным дифракционных методов. Косвенно симметрия может быть определена значительно проще, например, по числу геометрических изомеров, по данным поляризованных электронных спектров поглощения, ЭПР, ГРС и др.

Иногда можно предсказать симметрию координационной системы на основе общих представлений об изотропности пространства. Они позволяют, например, утверждать, что в системе типа МАб с центральным характером взаимодействия М-А одинаковые атомы или группы атомов А должны занимать эквивалентные положения. Вывод отсюда о максимальной симметрии системы неправомерен, так как, во-первых, в реальных случаях взаимодействие М-А, вообще говоря, не является центральным (из-за квантовых эффектов, приводящих к образованию л-, б- и т. д. связей) и, во-вторых, эквивалентность положений может реализоваться не за счет эквивалентных координат, а за счет эквивалентной динамики. Действительно, если хотя бы один лиганд А отличается по положению от остальных, то ввиду их идентичности (и изотропности пространства) можно указать еще по крайней мере пять структур, полностью эквивалентных данной, в которых другие лиганды А будут занимать поочередно выделенное положение данного, и равновесная картина окажется усредненной по этим пяти структурам. Однако такая ситуация выходит за рамки рассматриваемых здесь одноминимумных систем и примыкает к системам, обсуждаемым в разделе VIII. 2.

Закона максимальной симметрии в природе, насколько нам известно, не существует*. Возможные симметрии регулируются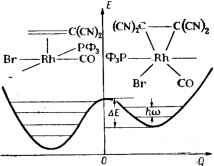

* С точки зрения такого закона у человека должно быть два сердца - с левой и с правой стороны.

законом минимума энергии. С точки зрения последнего симметрия ядерной конфигурации в устойчивом состоянии соответствует минимуму адиабатического потенциала.

Изомеры, таутомеры, конформации

Интересная ситуация возникает тогда, когда в системе, хотя и имеется только один абсолютный минимум адиабатического потенциала, но к нему близко примыкают другие, менее глубокие минимумы. В этом случае образуются и существуют различные соединения одинакового состава, которые известны под названиями изомеров, таутомеров, конформации и

Эти термины получили широкое распространение в химической научной литературе, однако их физический смысл недостаточно четко определен. В частности, предполагается существование различного электронного строения соединений с одной и той же ядерной конфигурацией (таутомеры), что противоречит адиабатическому приближению (раздел (VI. 1). Со-

гл-асно последнему, если речь идет об одном и том же электронном (основном) состоянии, электронная конфигурация может измениться только за счет изменения конфигурации ядер [см. уравнения (VI. 3) и (VI. 9)]. Поэтому необходимо допустить, что таутомеры (как и изомеры, и конформации) отличаются не только электронной, но и ядерной конфигурацией.

Корректное определение физической величины, как уже отмечалось (раздел 1.1), должно содержать (явно или неявно) указание на возможность ее экспериментального наблюдения. Рассмотрим в этой связи, каким условиям должны удовлетворять изомеры, таутомеры, конформации или другие образования одинакового состава, чтобы они могли быть различимы экспериментально. Прежде всего, в соответствии со сказанным выше, эти образования должны различаться ядерной конфигурацией. Последние приобретают смысл только в том случае, если они соответствуют минимумам адиабатического потенциала. Поэтому первое условие различимости двух молекул одинакового состава таково: для каждой из них адиабатический потенциал должен иметь свой минимум. На рис. VIII. 1 такие два минимума изображены вместе с примером двух изомеров (конформации) [397].

Рис. VIII. 1. Возможная форма адиабатического потенциала для двух различных молекул одинакового состава, каждой из которых соответствует свой минимум с глубиной Л£ > 2ЙЮ. Конкретный пример взят из работы [3971 (Ф-феннл).

Однако условие наличия минимумов для каждой ядерной конфигурации необходимо, но не достаточно. Если эти минимумы недостаточно глубоки и, следовательно, барьеры между ними невелики, то система, строго говоря, не является стационарной - она совершает непрерывные переходы между минимумами. В этом случае в зависимости от метода измерения конфигурации отдельных минимумов могут оказаться неразличимыми (см. раздел VIII. 2). Они буДут принципиально неразличимы, если время жизни отдельной конфигурации т будет меньше или порядка периода колебаний в минимуме адиабатического потенциала 7 , т с< 7 . Поэтому вторым необходимым условием различимости конфигурации (тауто-меров и т. д.) должно быть условие т 7 . Это условие удобнее записать в терминах частоты, или, еше лучше, величины барьеров и квантов колебаний. Учитывая, что 2лГ- = со, а т = йб~ и принимая во внимание формулы для частоты туннелирования [29, с. 209]: бйшехр(-Af/fico), где k - коэффициент порядка I, а - глубина минимума, получаем:

-2 (VIII.1)

Таким образом, только тогда, когда двум конфигурациям соответствуют два различных минимума адиабатического потенциала с (наименьшей) глубиной, примерно в два раза большей кванта колебаний в минимуме, имеет смысл говорить, что эти конфигурации соответствуют двум образованиям одинакового состава (изомерам, таутомерам, конформациям и др.).

0::обенности стереохимии координационных систем

Стереохимия, определяемая взаимным расположением атомов в системе, непосредственно связана с симметрией системы, хотя последняя носит более обший характер (при одной и той же симметрии может быть разная стереохимия; например, тетрагональной симметрией С4 обладают и квадратная пирамида, и бипира-мида, и т. д.). Как и симметрия, стереохимия определяется конфигурацией ядер в минимуме энергии адиабатического потенциала с учетом возможного влияния их динамики.

Для определения минимума энергии необходимо решить задачу адиабатического приближения (глава VI). Полные неэмпирические решения такой задачи довольно редки в практике исследований, так как выполнение их очень затруднительно. При расчетах электронного строения ядерная конфигурация (стереохимия) обычно не вычисляется, а предполагается известной по другим, чаше всего эмпирическим, данным. В некоторых случаях для уточнения расположения атомов в простых системах расчеты электронного строения и энергии проделывают для ряда близких значений коор-вднат ядер, а затем сравнением выбирают то из решений, которое аает минимум энергии. Такие расчеты в настояшее время уже довольно часты, некоторые из них обсуждались в разделе V. 5-

Какие электронные факторы влияют на стереохимию? Довольно широкое распространение имели представления Полинга, основанные на методе валентных связей, согласно которым стереохимию можно определить по типу гибридизации, которая требуется для объяснения электронного строения комплекса с Данным числом электронов [398,399]. К ним примыкают и представления Джилеспи и Нихольма [400] о роли неподеленных пар в стереохимии, основанные на качественных представлениях Сиджвика и Поуэла. Согласно последним неподеленная пара электронов играет такую же отталкивающую роль, как и дополнительная валентная связь. Однако в свете сказанного ранее (раздел 1.2) об особенностях электронного строения координационной химической связи, как трехмерно делокализованной, ее описание посредством локализованных валентных связей, вообще говоря, неадекватно действительности. Но представление о роли неподеленных пар оказывается более общим, так как последние могут фигурировать и в методе МО - в виде несвязывающих (или почти несвязывающих) МО (раздел V. 3).

При рассмотрении координационной системы в приближении теории кристаллического поля или метода МО ЛКАО все электронные факторы в стереохимии выражаются через изменения энергетических уровней при изменении конфигурации ядер. Одна из таких характеристик - энергия стабилизации кристаллическим полем (табл. IV. 10 и IV. И), на основе которой можно получить некоторые сравнительные данные по предпочтительной стереохимии и относительной устойчивости (раздел IX. 1). Однако в стереохимии помимо чисто электронного фактора - экстрастабилизации - важную роль играет основной вклад в устойчивость (притяжение ли* гандов к центральному иону в представлениях теории кристаллического поля или преобладающий вклад электронов на связывающих орбиталях в методе МО) и отталкивание остовов (раздел IX. 1). Сравним с этой точки зрения различные типы координации одного и того же переходного металла с одним и тем же типом лигандов.

Основной вклад в устойчивость, согласно теории МО, как уже указывалось, вносится электронами, занимающими связывающие молекулярные орбитали. Для октаэдрических комплексов таких электронов 12, а для тетраэдрических и квадратных - только 8 (раздел V. 3). Поэтому можно предположить, что основная часть устойчивости, обязанная своим происхождением образованию связывающих молекулярных орбиталей, больше всего у октаэдрической координации *. К такому же выводу можно прийти, исходя из представлений теории кристаллического поля: электростатическое притяжение шести лигандов больше, чем четырех. С другой стороны, второй фактор - отталкивание остовов между собой - действует в обратном направлении. Оно тем больше, чем больше

* Не следует думать, что эта часть устойчивости октаэдрических комплексов точно в Ve = /2 раза больше, чем у тетраэдрических или квадратных, так как энергии молекулярных орбиталей в этих случаях также различаются между собой.

Лигандов и, следовательно, понижает устойчивость больше всего у октаэдрической координации. Только сравнением всех трех факторов- основного вклада в устойчивость, дополнительной стабилизации кристаллическим полем и взаимного отталкивания лигандов - можно решить, какая координация наиболее устойчива. Очевидно, что результат такого сравнения окажется зависимым от природы лигандов.

Особый интерес представляет сравнение тетраэдрической и квадратной конфигураций, так как основная часть устойчивости в этих случаях может считаться примерно одинаковой. На основе данных табл. IV. 11 можно сделать вывод, что во всех случаях квадратная конфигурация дает большую экстрастабилизацию кристаллическим полем, чем тетраэдрическая. С другой стороны, для тетраэдрической конфигурации лигандов их взаимное отталкивание меньше, чем для квадратной. Поэтому последняя может оказаться более устойчивой лишь при значительной разнице в дополнительной стабилизации. Такой случай имеет место для центральных ионов с электронными конфигурациями d, d\ d и d. Действительно, например комплексы Ni (II) (#) (координационное число 4) в большинстве случаев квадратные [401]. В редких случаях тетраэдрических комплексов Ni (II) [например, Ni(P(C6H5)3)2Cl2] лиганды столь громоздки, что образование таких комплексов со всей очевидностью объясняется тем, что в квадратной конфигурации стерическое отталкивание преобладает над экстрастабилизацией.

В случаях, когда речь -идет о кристаллическом состоянии, в котором влияние соседей на данный комплекс нелья считать малым, оно должно быть принято во внимание наряду с основными факторами при исследовании возможной координации данного иона. Именно .влиянием следующих координационных сфер можно объяснить образование тетраэдрического комплекса Ni (II) в комплексе [As(C6H5)3CH3][NiCl4].

Следует отметить случаи, когда возможно образование я-орби-талей. Увеличение количества лигандов, образующих я-связи с центральным атомом, вообще говоря, ведет к повышению устойчивости связей. Отсюда было сделано неправильное заключение, что в соединениях с ненасыщенными лигандами координационное число должно быть большим и что, например, комплексы Zn (II), которые с алифатическими аминами являются тетраэдрическими, с ароматическими аминами должны стать октаэдрическими [402]. С учетом приведенных выше соображений повышение устойчивости связей не всегда ведет к повышению устойчивости комплекса в целом, ибо должно быть принято во внимание еще и стерическое отталкивание между лигандами, которое при увеличении координационного числа увеличивается. Замена алифатического амина на ароматический (например, аммиака на пиридин) может лишь усилить этот стерический эффект. Как было показано непосредственным рент-геноструктурным исследованием [403], комплексы ZnCl2-2n- и CdCb 2п-толуидин являются тетраэдрическими и аналогичны

[Zn(NH3)2Cl2].

<

<

a. я

я S (О га

- я . я га

Е а: о. X Ч

Я а: r=f к

J7 <и m га S

И ТО V

G ° g с

га а.

а. я

m га а. t-

Я s s