u о а: о

S: 0,6

0,8 0,6 0,4 0,2

т-I-I-г

d i

I м м

/Л,

т-I-I-

-Ю-5 О 5 -Ю-5 О 5 -W-5 О 5 -IDS О 5

0,6 0,4 0,2 у О

*Т I п г

-- d I д

I I I I

I I I I

IIIII

-Ю о 10 -Ю о 10 -Ю о 10 -10 о 10

б -

-15-10-5 0-5

5-5 О Частота

5-15 -10 -5 О 5

VII.4. СПЕКТРЫ ЛЮМИНЕСЦЕНЦИИ. БЕЗЫЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ. ЛАЗЕР-ЗФФЕКТ

Люминесценция. Флюоресцендия и фосфоресценция

Наряду с электронными спектрами поглощения спектры люминесценции оказываются важным средством исследования электронного строения координационных соединений. Из приведенной на , рис. VH. 1 схемы расположения адиабатических потенциалов видно, что частота в максимуме полосы люминесценции Q2, соответствующая электронному переходу из равновесной конфигурации (точки минимума) возбужденного состояния вертикально вниз (в приближении Франка - Кондона), меньше частоты максимума поглощения. Смещение максимумов поглощения и люминесценции, называемое стоксовым, равно:

q2 = Q,-aM , (VII. 37)

При этом предполагается, что после электронного возбуждения в точку Р, в которой возбуждены также и колебательные состояния, система успевает передать колебательное возбуждение другим степеням свободы (другим колебаниям или окружающим атомам- процессы релаксации) прежде, чем произойдет обратный электронный переход с эмиссией кванта электромагнитного излучения (так называемая равновесная люминесценция), что, как правило, действительно наблюдается.

Во многих координационных системах разность Qi - Q2 Для широких полос (большие значения параметра а) столь велика, что для поглощения в видимой области люминесценция попадает в инфракрасную область. Иная ситуация складывается в случае узких полос, для которых Q2 Qi- Как было показано ранее (стр. 243), узкие полосы возникают при переходах между термами одной и той же орбитальной электронной конфигурации. Такие термы чаще всего отличаются спиновой мультиплетностью (хотя это и не обязательно), и в этом случае переход окажется интеркомбинационным.

Рис. VII. 11. Интенсивности электронных А - Т-переходов в линейной Т - /г-задаче, как функции частоты, температуры, константы линейной связи В и параметра уширения а (все величины в единицах йсо) [267, с. 78]:

Для люминесценции это обстоятельство существенно потому, что возникшее возбужденное состояние оказывается относительно долгоживущим (метастабильным) из-за очень малой вероятности интеркомбинационного перехода (стр. 253). В таком случае люминесценция носит характер фосфоресценции (т. е. свечения с достаточно большим запаздыванием) в отличие от случая переходов между термами одинаковой мультиплетности, для которых она является простой флюоресценцией. Иллюстрацией происхождения люминесценции в координационных системах может служить хорошо изученный пример окта-

£2

e(Q)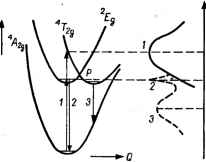

Рис. VII. 12. Адиабатические потенциалы для иона Сг+ в октаэдрическом комплексе и электронные переходы:

/-поглощение; 2-фосфоресценция; 3-флюоресценция. Справа показаны кривые поглощения и эмиссии (последняя пунктиром).

эдрических комплексов хрома (1П) [377].

На рис. VII. 12 представлена схема адиабатических по--тенциалов основного M2g(2g)-и первых возбужденных Egihsy- и %g(2g)(%)-электронных термов такого комплекса, типичного при кислородном октаэдрическом окружении иона Сг *, с одновременным показом полос поглощения и люминесценции [377]. После поглощения в широкой полосе M2g->*r2g система ре-лаксирует ак в основное колебательное состояние того же возбужденного терма Tig, так и в соседнее электронное состояние Eg, которое пересекается с Tzg. Последующие переходы *T2g-*A2g и Eg-*A2g с излучением и есть источник наблюдаемых полос люминесценции. При этом, в соответствии со сказанным выше, первому из них отвечает широкая полоса флюоресценции, а второму - узкая полоса фосфоресценции. Релаксационный переход *r2g Eg, носящий характер безызлучательного электронного перехода (см. ниже), как показывают расчеты, при низких температурах, более вероятен, чем только колебательная релакса- ция на том же уровне Tzg [352]. Поэтому с понижением температуры в этом случае фосфоресценция должна преобладать над флюоресценцией.

Анализируя влияние различных лигандов на взаимное положение M2g-, Tig- 2£g-TepM0B в комплексах хрома и на наблюдаемую при этом люминесценцию, Шлэфер с сотрудниками [377] предложили эмпирическое правило, согласно которому с ростом параметра расщепления кристаллическим полем А (в данном случае-частоты перехода M2g->*r2g), т. е. с перемещением лиганда вправо в спектрохимическом ряду, убывает вероятность флюоресценции и растет вероятность фосфоресценции Это можно иллюстрировать следующим полученным в работе [377] рядом (знаки <

относятся к величине Д): Вг < С1< F <

Только флюоресценция

Флюоресценция и фосфоресценция или только флюоресценция

<N<C

Только фосфоресценция

(VII. 38)

Это правило относится к случаю одинаковых лигандов (точнее, одинаковых ближайших к центральному атому) и не выполняется для случая смешанных лигандов. Аналогичная случаю комплексов Cr(III) люминесценция встречается также в соединениях V(II) [376], Mo (III) и др. [356, ch. 9].

Особенно интересны случаи люминесценции комплексов лантаноидов, в которых по зависимости f - /-перехода от состава лигандного окружения можно судить о характере связи металл - лиганд (см., например, [378]).

Для расчета формы полос равновесной люминесценции можно воспользоваться описанным в разделе VII. 1 полуклассическим приближением. В последнем она описывается функцией формы полосы Fi2(Q), которая получается из (VII. 11), если подставить в него выражениеp2(Q)exp(-fiQ/Г) вместо pi(Q) [374]. При наличии электронного выр£)ждения особенно интересно исследование поляризованной люминесценции, которая позволяет в ряде случаев определить характер минимумов адиабатического потенциала вырожденного терма, переходы в которых отличаются правилами отбора по поляризации света [284, 379].

Колебательная релаксация и безызлучательные электронные переходы

Теория люминесценции в значительной степени использует такие понятия, как вероятности релаксационных и электронных безызлучательных переходов. Действительно, можно легко показать, что интенсивность люминесценции, например рассмотренного выше перехода Eg-ig (см. рис. VII. 12), определяемая заселенностью возбужденного fg-TcpMa, зависит от соотношения между пероятностями колебательной релаксации на r2g-TepMe и безызлучательного электродного перехода Tgg Eg, а также от конкурирующих с люминесценцией безызлучательных переходов *Г2gv*Л2g и fgN-Mgg. Колебательную релаксацию следует понимать как передачу энергии возбужденных колебаний данного типа другим колебательным степеням свободы (или другим частицам при столкновениях) с установлением между ними термодинамического равновесия. В гармоническом приближении колебания не взаимодействуют между собой, поэтому колебательная релаксация происходит лишь благодаря ангармонизму колебаний. Последний становится существенным с ростом заселения более высоких колебательных состояний, т. е. с ростом температуры. Отсюда следует сильная зависимость вероятности колебательных релаксационных переходов от температуры,

Безызлучательный электронный переход имеет более сложную природу и наглядно может быть интерпретирован как переход электронной энергии в колебательную по причине неполной стационарности электронных термов. При определенип электронных термов системы в адиабатическом приближении отбрасывают некоторые малые члены полного гамильтонианг, которые названы членами неадпабатичности (стр. 192-195). Последние можно затем рассматривать как малое возмущение W, под влиянием которого система с какой-то вероятностью может перейти из одного стационарного в адиабатическом приближении состояния в другое. По правилам квантовой механики вероятность такого перехода определяется величиной квадрата матричйого элемента возмущения:

1Г,2= JtrF.dT (VII. 39)

Возмущением, вызывающим безызлучательный переход, может служить не только оператор неадпабатичности, но и другие неучтенные при определении электронных состояний взаимодействия, например, спин-спиновое или спин-орбитальное. Учет последнего неизбежен при определении безызлучательного перехода между состояниями разной спиновой мультиплетности (как, например, в рассмотренном выще переходе Iggg), так как в противном случае интеграл (VII. 39) из-за независимости W от спина равен нулю.

Соблюдение закона сохранения энергии при безызлучательном переходе требует, чтобы при этом два комбинирующих электронных терма имели совпадающие (или близкие) электронно-колебательные уровни энергии. Это возможно, когда их адиабатические потенциалы достаточно близко подходят друг к другу [иначе интеграл (VII. 39) мал].

Другими словами, безызлучательному переходу благоприятствует сближение термов (для случая, приведенного на рис. VII. 12 с этой точки зрения безызлучательные переходы

более вероятны, чем Eg *2g).- После перехода системы с верхнего адиабатического потенциала на нижний вблизи точки их пересечения система окажется в высоковозбужденном колебательном состоянии нижнего терма, после чего Колебательная энергия рассосется по другим степеням свободы, посредством колебательной релаксации. В итоге квант электронного перехода окажется размененным на несколько квантов колебаний - система нагреется (по этой причине безызлучательный переход иногда называют тепловым). Вполне понятно, что безызлучательный переход возможен также с нижнего терма на верхний - с последующим высвечиванием; тогда процесс носит характер термического свечения.

Теория безызлучательных переходов развивалась в последние годы главным образом для систем типа примесных центров в кристаллах (см. обзоры [352, 380]). Интересна, в частности, темпера-

турная зависимость вероятности безызлучательного перехода Р, которая приближенно имеет вид температурной активации процесса с потенциальным барьером [352]:

РРе- (VII. 40)

где A£ = (fiQ,)2/fi(fii -Q2).

Отсюда видно, что рост Р с температурой тем больше, чем больше стоксово смещение Qi -йгпри данном Qi (обозначения Ql и 2 см. на рис. VII. 1, стр. 243). В применении к молекулярным системам основные выводы теории остаются, хотя и имеется ряд особенностей, связанных, в частности, со значительно меньшей плотностью колебательных частот в молекулах, чем в кристаллах.

Квантовые генераторы света (лазеры)

Явления люминесценции с учетом безызлучательных процессов, представляют особый интерес в связи с широким их использованием в квантовых генераторах и усилителях (лазерах). Обширная литература по лазерам (см., например, [381]) позволяет, нам ограничиться здесь кратким освещением принципиальной сущности лазера и его связи с электронным строением координационных систем.

Приведенная выше схема люминесценции в октаэдрических кислородных комплексах хрома лежит в основе классической трехуровневой лазерной системы на ионах Сг+, замещающих ионы АР+ в корунде - наиболее распространенном рубиновом лазере. На рис. VII. 13: Ql-частота накачки; Q2 -рабочая частота. Решая соответствующие кинетические уравнения с учетом вероятностей всех излучательных и безызлучательных переходов (см., например, [382, с. 205]), можно показать, что при наличии внешнего излучения достаточной мощности частоты накачки Qi возможно получение стационарного режима, при котором заселенность возбужденного состояния Eg будет больше, чем для основного M2g. Так как поглощение квантов частоты 0.2 пропорционально заселенности М2й-терма, а вынужденное излучение той же частоты Qa пропорционально заселенности fg-xepMa, то под влиянием падающего излучения частоты Q2 система будет больше излучать, чем поглощать. В итоге отраженное или проходящее излучение окажется интенсивнее падающего, система будет обладать отрицательным коэффициентом поглощения *.

* Системы с отрицательной инверсной заселенностью- усилители и генераторы эпектромагнитных волн, принципиальная возможность которых вытекает из работ Эйнштейна 1917 г., были впервые разработаны и осуществлены Н. Г Басовым и А. М. Прохоровым, Гордоном, Цангером и Таунсом (см. [!82, с. 40]).

Рис. VII. 13. Уровни энергии и переходы в рубиновом лазере. Волнистой стрелкой показан безызлучательный переход.