->Q/

где Mi2 - матричный элемент перехода в состояние Wu (а не g). При этом в выражении для формы полосы (VII. 11) из-под интеграла выносится I М°2 f, а под интегралом остается дополнительный (по сравнению со случаем разрешенного перехода) фактор Qu, который сушественно меняет форму полосы и ее температурную зависимость, так что она становится зависимой и от частоты нечетного колебания со.

Вывод, аналогичный тому, который приводит к формуле (VII. 19) для разрешенного перехода, позволяет получить*

- cth Р

[(п -f 1) е-Р-Р/р, (г) + пе~Р1р2 (z)]

(VII. 32)

где в дополнение к приведенным выше обозначениям

£(0

(VII. 33)

fil -частота в максимуме полосы поглощения (рис. VII. 1):

Q, = Qo--2 о (* )

п + \

Eg - Ей - ha .

(VII. 34)

.Eg-Eu + Ы :[ехр(Йсо7АГ - 1]-

Эта формула получается в предположении, что только одна нечетная колебательная частота активна в разрешении перехода и только один дополнительный электронный уровень участвует с заметным весом в возмущении функции по (VII. 31). Из нее, в частности, видно, что нечетнке колебания существенно влияют i как на положения максимума, так и на интенсивность. При не очень больших частотах со в большинстве точек полосы можно взять pi рг, что приводит к появлению в (VII. 32) множителя ( + /2), который остается и после интегрирования по Отсюда следует важный вывод о том, что если переход разрешается за счет участия нечетных колебаний, то интенсивность его будет увеличиваться с ростом заселенностей этих колебаний п, т. е. с ростом температуры. По этому характерному увеличению силы осциллятора с ростом температуры (отсутствующему для других механизмов разрешения перехода) безошибочно идентифицируется d-d-переход, разрешаемый колебаниями.

Если переход разрешается нецентросимметричным (например, тетраэдрическим) расположением лигандов, то необходимое для перемешивания четных и нечетных состояний центрального иона

* Формула (VII. 32) получена по просьбе автора Ю. Е. Перлиным непосредственно из формул (23) и (24) его работы [366] (см, также [367]).

возмущение создается уже неподвижными в равновесных положениях ядрами, а не только ядерными смещениями. В этом случае переход окажется более интенсивным, но без указанной выше температурной зависимости интенсивности. В обоих рассмотренных случаях разрешение перехода вызвано влиянием лигандов и чем сильнее это влияние, тем более интенсивным должен быть переход.

Возможен, однако, механизм разрешения перехода, в котором участие лигандов несущественно, - это магнитно-дипольное и электрически-квадрупольное взаимодействие с электромагнитной волной. Как уже отмечалось, такие переходы значительно менее интенсивны (/ ~ 10 и 10 ), однако в тех случаях, когда состояния системы очень слабо связаны с колебаниями, магнитные дипольные переходы становятся определяющими наблюдаемую полосу.

VII.3. ПЕРЕХОДЫ С УЧАСТИЕМ ЭЛЕКТРОННО-ВЫРОЖДЕННЫХ ТЕРМОВ. РАСЩЕПЛЕНИЕ ЯНА-ТЕЛЛЕРА

Из изложенного выше в этой главе отчетливо следует вывод о весьма существенном влиянии форы адиабатических потенциалов электронных состояний, между которыми происходит переход, на форму полосы поглощения (или люминесценции). С другой стороны, в главе VI было показано, что наличие электронного вырождения приводит к резкому усложнению формы поверхности адиабатического потенциала. Поэтому следует ожидать, что наличие электронного вырождения у одного или обоих комбинируемых состояний сильно изменит ожидаемую форму noioc электронного перехода.

Рассмотрим сначала случай, когда одно из комбинируемых состояний является двукратно вырожденным Е-термом (переходы А-Е и Е-*А). Для линейной £-е-задачи вибронные уровни энергии определяли численно из решения системы вибронных уравнений (см. раздел VI. 4). Используя эти данные, можно вычислить интенсивности переходов на каждый из этих уровней Е-терма или из этих уровней на колебательные уровни невырожденного Л-терма. Таким образом были получены данные рис. VII. 6 [295], иллюстрирующего относительные интенсивности колебательных компонент в полосе переходов для А-*Е и Е->А (для нескольких значений безразмерной константы вибронной связи X = 2£ят/йсо). Из рис. VII. 6 видно, что полоса перехода А-*Е (огибающая колебательных компонент) имеет двугорбый вид, который можно интерпретировать как расщепление Яна-- Теллера (ср. с формой огибающей для переходов между невырожденными термами, рис. VII. 2). Для перехода Е-*А такого расщепления не возникает, что является следствием пренебрежения заселенностью возбужденных вибронных уровней исходного терма, верного лишь при Г = О (см. ниже).

Более общую (хотя и менее точную в частностях) информацию о форме полос электронных переходов в рассматриваемом случае

можно получить в обсуждаемом выше (разделе VII. 1) полуклассическом приближении, согласно которому функция формы полосы определяется формулой (VII. 11). Если подставить в нее выражения для адиабатических потенциалов в пространстве актив-

1 I I I h. ..

III..

\- !.......

iiiii...

2ДЕ

= 30

!.....iiilllliiiiii

III!

.....I

Ни.,

Рис. VII. 6. Интенсивность колебательных компонент и форма \ полосы поглощения (огибающая) для переходов А-*- Е и Е-*- А [295]. -Вертикальная стрелка указывает на положение бРсфононной линии частоты Q. -

НЫХ координат Q2 и Qs для А- и f-термов в линейном приближении [см. (VI. 25)]

e.(Q2.Q3) = Y(Q + Ql)

, , (VII. 35)

2 (Q2. Qi) = ii%+jK (Ql + Q±\A\ aJq] +

где Qo в этом случае - частота чисто электронного перехода при Q2 = Q3 = О, и произвести необходимые интегрирования, то получим;

Fl2 №) =

A2kT

a2kT

(VII. 36)

Кривая (VII. 36) изображена на рис. VII. 7, а. Она имеет глубокий провал до нуля при Q == Qq и в целом может интерпрети-

роваться как расщепленная эффектом Яна -Теллера. Величина расщепления пропорциональна V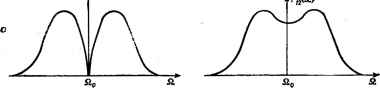

Рис. VII. 7. Форма полосы поглощения электронного А £-пере-хода в полуклассическом приближении линейной Е - е-задачи с учетом вибронного взаимодействия с е- и арколебаниями (toi и ai - частота последних и константа

связи с ними; X =.cth ; л i = а-а, =0; б-ЛХ > oJXj; в-АХ<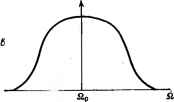

<а?Х

Первые расчеты полос поглощения в ян-теллеровских системах в иолуклассическом приближении проделан! ОБрайен [368], Мо-ран [369] и Тойодзава и Инуе [370].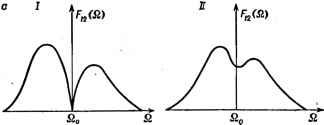

£? f is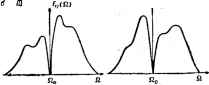

Рис. VII. 8. Форма полосы поглощения электронных перех одов Е-*-А (а) и £-> £ (б) в полуклассическом приближении линейной Е - е-задачи:

/-о,=0; -ai#0; III-Ai>A,; IV-A,<A, (Ai и Л,-константы линейной связи с е-колебаниями в основном и возбужденном £-термах).

Впоследствии эти расчеты усовершенствовались рядом авторов [371-374; 317, гл. IV; 267, ch. III]. В частности было показано (372], НТО с учетом влияния не принимаемых во внимание в формулах (VII. 35) и (VII. 36) полносимметричных колебаний (наиболее эффективных в уширении полосы в отсутствие электронного

вырождения) все острые элементы кривых поглощения сглаживаются (рис. VII. 7, б), а при очень сильной связи они могут с даже подавить ян-теллеровское

расщепление [372; 351, с. 122] (рис. VII.7,в).

Для переходов Е-*А соответствующие кривые приведены на рис. VII, 8, а. На первый взгляд может показаться, что они противоречат приведенным на рис. VII. 6 результатам, полученным на основе точного решения вибронного уравнения. Но как уже отмечалось, результаты рис. VII. 6 получены при температуре Г = О, при которой полуклассические результаты дают аналогичные кривые. Для Е-Е-переходов кривые имеют еще более сложный вид [372, 3731 (рис. VII.8,б).

Аналогичные выводы можно получить для переходов на трехкратно вырожденные Г-термы [370, 371]. В этом случае кривая поглощения существенно зависит от соотношения констант связи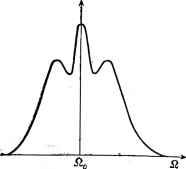

Рис. VII. е. Форма полосы поглощения электронного перехода А-*-Т в полуклассическом приближении Т - /-вадачи.

В =0,7

о, = 0,2/5 0,430 0,645 0,860 1,075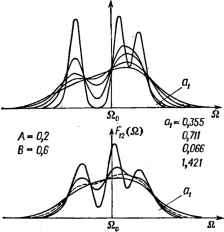

0,815 1,223 1,631

Рис. VII. 10. Зависимость формы полосы поглощения электронного А - Г-пере-хода в полуклассическом приближении линейной Т ~(е+ <2)-задачи от констант вибронной связи Л, В и й! с е-, t- и полносимметричными арколебаниями [371].

А, В и а\ С е- ti- и полносимметричными ai-колебаниями. При пре- имущественной связи с е-колебаниями (линейная Т - е-задача, раздел VI. 3) полоса Л->Г перехода не расщепляется, хотя адиабатический потенциал 7-терма при этом существенно расщеплен

£64

(рис. VI. 7). Этот случай показывает сколь осторожно нужно пользоваться наглядными картинками при анализе сложных явлений.

При преимущественной связи с 2-колебаниями (Т - 2-задача) кривая поглощения А-Т расщепляется на три (рис. VII.9). В общем случае линейной Т- (е + г)-задачи результаты зависят от упомянутого соотношения констант связи и иллюстрируются на рис. VII. 10 для некоторых частных случаев, полученных численным интегрированием выражений полуклассического приближения [371]. Для линейной Т - 2-задачи численные результаты получены [297] также на основе точного решения вибронных уровней, приведенного в разделе VI. 4; некоторые примеры полученных кривых иллюстрируются на рис. VII. П. (О форме полос поглощения и люминесценции в системах с эффектом Реннера см. в работах [373, 374]).

Из приведенного краткого обсуждения отчетливо видно, что кривые поглощения, обязанные электронным переходам с участием вырожденных термов, в общем случае очень сложны и не могут быть аппроксимированы одногорбой кривой. Учитывая, что наличие электронного вырождения в основном или возбужденном состояниях является типическим случаем (а отсутствие его - исключением), мы приходим к выводу о невозможности в общем случае каждому максимуму поглощения (или люминесценции) ставить в соответствие уровень энергии системы. С учетом достижений теории, кратко изложенных в этом и предыдущем разделах, полная интерпретация электронного спектра хорошего разрешения становится значительным исследованием, позволяющим получить весьма ценную информацию об электронном и вибронном строении системы.

Вибронные эффекты в переходах с участием электронно-вырожденных термов проявляются непосредственно и в бесфононных линиях (стр. 248). Так как последние (см. выше) довольно узки, в них может отразиться тонкая структура вибронных уровней, получаемых в результате решения вибронных уравнений (VI. 13). В частности, можно ожидать, что рассмотренное в разделе VI. 4 инверсионное (туннельное) расщепление проявится в виде соответствующего расщепления бесфононной линии перехода на электронно-вырожденный уровень в поглощении или люминесценции. Такое расщепление действительно наблюдалось в ЛЕ-перехо-дах в системах [375]: g

Eu2+-CaFz................. 15.3

Eu*+-SrFs................. 6.5

Sm2+-CaFs ................ 27

Sm2+-SrFz................. 26

Интерпретировано оно было как обязанное туннельному расщеплению в работе [336].

Расщепление бесфононной линии ~40 см-* наблюдалось также в М1-> Гг-переходе системы V*+ -MgO [376]. Объяснение его как вызванное туннельным расщеплением в 72-терме пока еще нельзя считать окончательным, хотя его ян-теллеровская природа не вызывает сомнений,