поляризацию полосы поглощения. Правила отбора для этого случая рассмотрены в разделе III. 4, стр. 63.

Поляризованные электронные спектры монокристаллов (чаще всего спектры отражения) представляют существенный интерес, поскольку позволяют получить дополнительную информацию об электронном строении соединения [356. ch. VI; 357, 358]. Использование поляризованных спектров для исследования вращения плоскости поляризации веществом, дисперсии оптического вращения и циркулярного дихроизма см. также в обзорах [359, 360].

Vll.2. /-(/-ПЕРЕХОДЫ СПЕКТРОХИМИЧЕСКИЙ И НЕФЕЛОКСЕТИЧЕСКИЙ РЯДЫ

Происхождение и особенности </- /-переходов

В соответствии с отмеченной ранее (стр. 13-15) ролью d- и /-состояний ц. а. в образовании координационной-связи электронные переходы с участием этих состояний являются наиболее важ-

5 I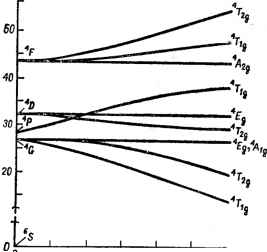

5000 10000

й,СМ-

/5000

Рис. VII. 4. Диаграмма уровней энергии нона Мп+ в кубическом кристаллическом поле как функция параметра Д [2].

ными для координационных соединений. Большой интерес представляют переходы между состояниями, происходящими от исходной d конфигурации, которые часто называют d-d-переходами.. Как наиболее длинноволновые, эти переходы попадают в видимую и прилегающую к ней области, определяя цветность (окраску.) соединения. Являясь предметом специальных исследований, начатых в 20-х годах настоящего столетия Шибатом и развитых Цутидой,-

€00 500

а.ммк

0,03 0,02 0,01

20000

25000 см

Кишом, Линхардом, Хартманом и другими (см. [1-б, 8-11]), спектры поглощения в видимой и прилегающих к ней областях вместе с магнитными свойствами послужили экспериментальной основой для создания теории кристаллического поля (глава IV), в которой они получают естественное истолкование.

Обратимся к выводам разделов IV. 2-IV. 5. Наиболее общая картина расщепления атомных термов в кубическом поле лигандов получается в виде диаграммы уровней- энергии как функции параметра расщепления Д (см. диаграммы Танабе - Сугано, рис. IV. 10, стр. 96). Из этой картины уровней можно найти одну из наиболее важных характеристик спектра - положения максимумов полос. Для этого, проводя на диаграмме вертикаль через точку - значение параметра Д для рассматриваемого комплек- са, мы найдем ожидаемые положения максимумов полос, как ординаты точек пересечения уровней энергии диаграммы с этой вертикалью. Искомое значение Д можно найти, например, по известному положению одной из полос.

в качестве примера рассмотрим рассчитанную Оргелом [2, р с. у11.5. Спектр поглощения вод-с. 103] диаграмму уровней иона ного комплекса IAv?+.

Mn2+(cf) (рис. VII.4) и сравним

ее с экспериментальным спектром поглощения (рис. VII. 5) [361]. Легко видеть, что при Д 9000-10000 см все наблюдаемые максимумы могут быть интерпретированы как отвечающие электронным переходам из основного состояния Mig в соответствующие возбужденные, указанные на рис. VII. 5. При этом получается хорошее относительное согласие между рассчитанными и экспериментальными данными.

Наблюдаемые для этого случая ширины полос также могут быть. объяснены с привлечением результатов предыдущего раздела. Действительно, основное невырожденное орбитальное состояние Aig происходит от наполовину заполненной d-оболочки центрального иона (d) с конфигурацией в октаэдрическом поле ihgViegy. Поэтому переходы Aig->*Tig{t2g)*(eg) и M,g - --**T2git2g)*{eg) с изменением этой конфигурации дают наиболее широкие полосы. Другие состояния, переходы в которых дают остальные приведенные на рис. VII. 5 полосы (*£g, Mjg, *72g и *Eg), происходят от той же электронной конфигурации (2g)(eg) что и основное состояние, и поэтому эти полосы значительно уже.

Непосредственно определяемые из диаграммы уровней производные dE/dA (по наклону кривых в данной точке) позволяют провести более детальную дифференциацию полос по ширинам. Как видно из рис. VII. 4, для основного состояния Mig dEJdA = О и поэтому уширение определяется абсолютным значением йСг/Д

для возбужденного состояния. Последние находятся непосредственно и примерно равны: 1; 0,8; 0; 0; 0,2; <0,1; 0,9 для состояний *hg(G), *T2g{G), *Eg(G), M (G). EAD) и hg(P). соответственно. В такой же последовательности порядков величин (хотя и не точно пропорционально) следуют ширины наблюдаемых полос поглощения (см. рис. VH. 5), качественно подтверждая выводы, приведенные ранее (стр. 244).

Заметим также, что все эти переходы, запрещенные по четности и по спину, попадают в одну группу по интенсивности, имея одинаковый порядок величины силы осциллятора.

Два параметра теории, Л и я-два типа рядов лигандов - спектрохимический и нефелоксетический

Из рассмотренного примера иона IAn+{d) в слабом октаэдрическом поле видно, что знание диаграмм уровней энергии как функции Д для данного комплекса является вполне достаточной основой для общей интерпретации наблюдаемых в нем спектров, если речь идет об электронных переходах d-rf-типа.

Приведенные на рис. IV. 10 диаграммы Танабе - Сугано, рассчитанные для электронных конфигураций (п = 2,3,4,5,6,7,8) (для одноэлектронных конфигураций и d простые схемы расщепления известны непосредственно из рис. IV. 2 и IV. 3), могут быть использованы для любого кубического -комплекса, если

Таблица VII.2

Значения параметра кристаллического поля Л для комплексов ряда переходных металлов с различными лигандами

известно отношение Л/В, где В - параметр Рака (стр. 42). Отсюда видно, что в интерпретации спектров два параметра -Д и В, - зависящие от свойств центрального атома и лигандов, играют решающую роль.

Зависимость Д от свойств центрального иона отчасти обсуждалась ранее (раздел IV. 5). Для З-элементов величина Д возрастает с ростом заряда, будучи величиной 10000 см для Ме+ и 20000 CM- для Ме+. С переходом от 3d- к Ad- и 5с?-эле-ментам величина Д также растет, достигая ~40 ООО см .

Зависимость от характера лигандов более разнообразна, что видно из табл. VII. 2, составленной по данным Иоргенсена (см. [6, 8, 9]). При этом, однако, отчетливо выявляется определенная закономерность возрастания Д при движении по таблице слева направо, независимо от природы ц. а. Это позволяет установить так называемый спектрохимический ряд, характеризующий в какой-то мере возрастающее влияние лигандов:

Bi- < СГ < YОх - <Н20 < NHs < En < CN (VII. 29)

Это определение спектрохимического ряда, вообще говоря, не совпадает с устанавливаемым эмпирически по гипсохромному эффекту, т. е. по смещению первой полосы поглощения в ультрафио--летовую область при замещении предыдущего в ряду лиганда в комплексе на последующий *. Действительно, такое смещение полосы будет свидетельствовать об увеличении Д только в случае, если она отражает простые электронные переходы типа tz-e. Но как видно из диаграммы Танабе - Сугано, с ростом Д частота некоторых переходов растет, а других убывает. В частности, в случае рассмотренной выше диаграммы f\n*{d), первая длинноволновая полоса, соответствующая переходу Mig->-7ig (изменение электронной конфигураций Cg -> tig), с ростом Д смещается в длинноволновую, а не коротковолновую область. Кроме этого, с ростом Д система уровней энергии может перейти из высокоспиновой области в низкоспиновую (см. область изломов кривых на диаграммах Танабе - Сугано, рис. IV. 10) с совершенно иным характером электронных переходов.

Поэтому эмпирически установленные по гипсохромному эффекту спектрохимические ряды в общем случае не могут отражать закономерности изменения параметра Д при лигандных замещениях. Такую закономерность можно получить по гипсохромному эффекту только в полосах переходов типа tie в комплексах

Оксалат. 2* Этилентетраамнн. з Этилеидиамнн,

* Такой гипсохромный ряд имеет вид:

Г < ВГ < СГ - SCN- ~ щ < (CHp)Ps; <

< F- < (C2He)2NCS2 < (NH2)2CO < ОН- < (СОО)Г ~ ~ Н2О < NCS < КНгСНгСОО < NCSHg* ~ nh3 ~ C5H5N < < NHjCHCHNH ~ SO- < NH,OH < NO, < Н ~ CH < CN 9 П. Б. Берсукер

определенного спинового состояния (низкоспиновые или высоко-спиновые).

Другой параметр системы -Б,- характеризующий межэлектронное взаимодействие в системе (стр. 42), также оказался зависящим от лигандов. Если сравнить значение В для свободного иона й для того же иона в комплексе, то в последнем случае он оказывается всегда меньше. Это уменьшение параметра В, отражающее уменьшение взаимного отталкивания электронов, объясняется расплыванием электронных облаков (делокализацией электронов на большие области) вследствие образования молекулярных орбиталей, и в такой интерпретации оно находит количественное обоснование [101]. Подробно изученный Иоргенсеном [10, ch. 23; 362] эффект был назван нефелоксетическим, что в переводе с греческого означает эффект расплывающегося облака.

Таблица VH.3

Значения параметра Рака В для свободных нонов и комплексов ряда переходных металлов с различными лигандами

Электронная

конфигурация

Лнгавд

свободный ион

3d3 3d 5 3d5 3de

.ад

Fe3+

950 850 -1000 Л 050 -800 660 1030 ИЗО

6Вг~

300 250

400 300

В табл. VII. 3 приведены некоторые значения В для свободных ионов и комплексов, установленные эмпирически по спектроскопическим данным. Введя отношение р = Вкомпл/св. и, можно расположить лиганды по величине соответствующего им параметра р (для данного металла в одной и той же степени окисления) в так называемый нефелоксетический ряд:

F > НгО > (NH2)2CO > КНз > (СОО)- > NCS > СГ ~

~ CN > Вг > (C2HbO)2PS2 ~ S2- ~ Г > (C2H50)2PSe2 , (VII. 30)

Очевидно, поскольку делокализация электронов тесно связана с ковалентностью,. нефелоксетический ряд, отражая рост делокализации электронов слева направо, в какой-то мере отражает и рост ковалентности связей в том же направлении. В этом отношении нефелоксетический ряд дает более определенную химическую информацию, чем спектрохимический.

Можно показать, что введенный выше параметр нефелоксетич-пости р не является однозначным для данного соединения. Действительно, так как значение Вкомпл определяется из спектроско-

пических данных (см. раздел II. 2), оно может оказаться различным для разных электронных переходов. Поэтому обычно различают [10, с. 302]: Б(Уз-*Уз); В(Уз-*\5) и B(Y5->Y5). где Уз и Ув символизируют eg- и <2е-конфигурации в октаэдрическом комплексе (в обозначениях Бете Гз = Е и Г5 = 72, см. стр. 66) так что, например, уз->уз означает электронный переход внутри eg-конфи-гурации, а уз-*У5 - с переходом электрона с eg- на г-состояния и т. д., в соответствии с чем вводятся три нефелоксетических параметра, Рзз, Рз5 и Р55. Легко видеть, что число таких параметров можно увеличить, но это едва ли имеет смысл, ибо с ростом числа параметров, необходимых для интерпретации экспериментальных данных, последняя становится все менее определенной.

Интенсивности </- /-полос

По интенсивности rf-rf-переходы попадают в группу запрещенных по четности (см. табл. VII. 1) и, кроме этого, некоторые из них запрещены также по спину - как интеркомбинационные. Последние отделяются от первых непосредственно по существенно меньшей величине силы осциллятора. Снятие запрета по четности, как уже указывалось, в наиболее вероятном варианте вызвано влиянием лигандов - их нецентросимметричным расположением или нечетным колебанием (в случае симметричного расположения), перемешивающим четные и нечетные состояния центрального иона [363-365]. Помимо этого rf -rf-переходы могут оказаться разрешенными (с меньшей интенсивностью) как магнитно-диполь-ные или квадрупольные.

В разделе 111.4 методами теории групп проиллюстрировано, каким образом вовлеченные в электронный переход нечетные колебания делают интегралы матричного элемента дипольного момента (VII. 4) отличными от нуля. Ниже мы получим некоторые количественные соотношения для этого случая.

Рассмотрим электронный переход между двумя четными d-co-стояниями координационного комплекса с центром инверсии, полученные в адиабатическом приближении с учетом нулевого члена разложения электронно-колебательного взаимодействия в ряд по нормальным смещениям из-положения равновесия (VI. 7), и учтем линейные члены этого разложения, соответствующие нечетному колебанию Qu, в виде возмущения. Последнее приводит к тому, что к четным электронным состояниям примешается некоторое соседнее нечетное состояние Wu, так что волновая функция принимает вид:

+ ()о -

За счет нечетной примеси электронный матричный элемент электрического дипольного момента становится отличным от нуля.

о