ГЛАВА VII

ЭЛЕКТРОННЫЕ СПЕКТРЫ

Электронные спектры несут в себе важную информацию об электронном строении многоатомных систем, и задача состоит в том, чтобы, правильно выбрав характеристики спектра и параметры строения, установить однозначное соответствие между ними,

VII.1. ФОРМА ПОЛОС ЭЛЕКТРОННЫХ ПЕРЕХОДОВ

Качественная интерпретация колебательного уширения электронной полосы в приближении Франка - Кондона

Отличительная особенность электронных переходов в молекулярных системах состоит в том, что они, с одной стороны, зависят непосредственно (и примерно в одинаковой мере) от двух ее электронных состояний - начального и конечного*. С другой стороны, в отличие от атомов, энергии электронных термов молекул, между которыми происходит переход, сильно зависят от межъядерных расстояний и поэтому стационарными являются не электронные, а электронно-колебательные (или даже электронно-колебательно-вращательные) состояния.

На рис. vn. 1 показаны электронные энергии [адиабатические потенциалы (см. раздел VI. 1)] как функции обобщенных или нормальных координат для двух простейших состояний системы в отсутствие электронного вырождения, и соответствующие им колебательные состояния (горизонтальные уровни в минимумах). Уже это простое представление электронных термов посредством адиабатических потенциалов позволяет в наиболее простых случаях получить некоторые важные характеристики полос поглощения, непосредственно связанные с электронным строением.

Лрежде всего, примем во внимание принцип Франка-Кондона, согласно которому во время электронного перехода ядерная конфигурация системы не успевает измениться, так что переход совершается при неизменной конфигурации ядер, присущей исходному электронному состоянию. В соответствии с принципом Франка - Кондона, электронные переходы будут вертикаль-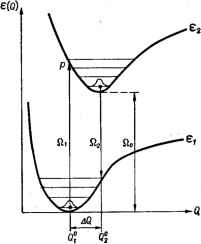

Зависимость от двух состоянии системы - характерная черта всех резонансных физических методов исследования.

ными , как это показано на рис. VII. 1. В связи с этим, как легко заметить, переход между термами не является чисто электронным, так как он меняет и колебательные состояния, и частота поглощаемого кванта ЬО, зависит от колебательного состояния исходного электронного терма. Меняется она примерно от Qj до Q2 за счет включения в переход различного числа колебательных квантов основного и возбужденного термов. С учетом температурной зависимости заселенностей колебательных состояний, различий вероятностей переходов и собственной ширины каждого перехода это приводит к тому, что в спектре поглощения вместо узких атомных линий наблюдаются широкие колоколообразные полосы с полушириной (шириной полосы на половине интенсивности) около Ql - 0,2.

Легко видеть, что эта полуширина непосредственно связана с различием в положении минимумов адиабатического потенциала в основном и возбужденном состояниях, характеризуемом величиной Щ = ф - Q2. Чем больше это различие, тем шире полоса поглощения. С другой стороны, различие равновесных межатомных расстояний в разных электронных состояниях определяется различием орбитальной электронной конфигурации в этих состояниях. Известно [348], что в координационных системах так называемые ионные радиусы, непосредственно отражающие равновесные межатомные расстояния, сильно зависят от чисел заполнения (п и т) различных rf-орбиталей электронной конфигурации (2) (е) . Поэтому изменения этих чисел -Дл и Дт -могут быть использованы для ориентировочной качественной оценки изменения равновесных межатомных расстояний при переходе от одного электронного состояния к другому.

Различают две группы электронных переходов в комплексах:

1. ДпО (Дт 0) -электронные переходы с изменением орбитальной электронной конфигурации, дающие широкие полосы поглощения (и люминесценции). Эти полосы остаются широкими и при низких температурах. Расчеты (см. ниже) позволяют оценить ширины этих полос от одной до нескольких тысяч см

2. Дп = Дт = 0 - электронные переходы без изменения орбитальной электронной конфигурации, например (но не только), интеркомбинационные переходы, дающие узкие линии поглощения с шириной 100 CM-j

Рис. VII. 1. Адиабатические потенциалы, колебательные.уровни и вертикальные электронные переходы.

Частоты: Qi-при поглощении; О,-люминесценции; Qe-чисто электронного перехода.

Заметим, что в случае заполнения /-оболочек равновесные межатомные расстояния слабо зависят от числа /-электронов из-за их слабого участия в связи. Поэтому переходы, связанные с изменением только /-орбиталей, в большинстве случаев дают узкие линии.

Более точную количественную характеристику рассматриваемого колебательного уширения можно получить, если известны диаграммы E = f(A) уровней энергии как функции параметра кристаллического поля Д (см. л)аздел IV. 5). Действительно, из рис. VII. 1 видно, что чем больше сдвиг минимумов основного и возбужденного состояний, тем больше энергия перехода Ш = = Е2 - Е1 зависит от межатомного расстояния Q, т. е. тем больше абсолютное значение производной d(bQ)/dQ = dEz/dQ- dEi/dQ. С другой стороны, производная dE/dA, очевидно, характеризует относительную чувствительность уровня энергии к изменению влияния лигандов или, при прочих равных условиях,- к изменению межатомных расстояний Q. Отсюда выявляется корреляция между колебательным уширением и величинами

d (bQ) d (Ш) dEj dEi dQ ~ dA dA dA

(VII. I)

Приведенное выше разделение всех полос на две группы по ширине получается в виде непосредственного следствия найденного соотношения в приближении кристаллического поля без учета взаимодействия между электронами. В этом случае можно написать для конфигурации (2) (е) (см. разделы IV.3-IV.5):

El = const]

+ til- Д

£г == constj - -g- А + 2 g- А

d(bQ)

dEj dA

-{m,- trii) -j- ( 2 - n,)

(VII. 2)

(VII. 3)

Отсюда видно, что если электронная конфигурация не меняется при переходе, то = пг = ni и [rf(ftQ)/rfA] = О и колебательного уширения не будет - полосы будут узкими. Для переходов с- изменением электронной конфигурации, например, с переходом одного электрона е -2> mi -т2=1, пг -ni = l и d(fifi)/dA=l, что дает широкую полосу.

: Приведенное объяснение происхождения широких и узких линий является первым этапом интерпретации электронных спектров. Рассмотрим некоторые примеры.

Переход Tg-Eg в комплексах типа [TiAeP* соответствует изменению электронной конфигурации (2g)- -(eg)l, Дп = -1, Дт = 1, т. е. он связан с появлением широкой полосы поглощения (или люминесценции при Tg-Eg), что согласуется с опытными данными [349].

Переходы A\g-*Tig, Alg-*T2g равно как и интеркомбинационные A\g-*.T\g и Aig-Tzg в низкоспиновых октаэдрических

системах с электронной конфигурацией (например, [Со (ЫНз)б]), связаны с изменением электронной конфигурации (2g)*-* >(/2g)(eg)4 поэтому все эти полосы получаются широкими [350].

Наоборот, интеркомбинационные переходы, происходящие от изменения только спина (t2g\y-*(hg\Y(.kg\), для которых Дм = = Дт = 0, например, переходы M2g->-£g в [Cr(H20)6] дают узкие линии поглощения. Примеры более тонкой дифференциации ширин полос поглощения приведены ниже.

Теория формы полосы поглощения*

Основные характеристики электронного перехода между двумя состояниями системы, описываемыми волновыми функциями -i и 11)2, определяются так называемым дипольным моментом перехода Mi2

JW,2= JitlitarfT (VII. 4)

где М -оператор электрического или магнитного (в зависимости от типа перехода) дипольного момента системы (аналогичное выражение можно написать для квадрупольных и других мульти-плетных переходов [252, гл. XII]). Для электрического дипольного

перехода ЛГ = Х Ягь {.Яь ri - заряды и радиусы-векторы частиц си-

->

стемы). Очевидно, что значение интеграла Мп существенно зависит от вида функций ti и v[2, так что для данного электронного перехода 1-)-2 оно определяется характером комбинируемых колебательных (и вращательных) состояний. Последние можно отметить зависимостью Mi2(Q), где Q -частота перехода. Зная

Mi2(Q), можно легко найти коэффициент поглощения света/Ci2(Q). Определим его, как обычно, из соотношения / = /оехр[-/Ci2(fi)/], где /о и / - интенсивности падающего и проходящего света, а / - толщина поглощающего слоя. Тогда [70, с. 230; 351, с. 53]

(VII. 5)

где - число поглощающих центров в единице объема.

Однако при наличии близких уровней с почти непрерывной

зависимостью Mi2(Q) имеет смысл ввести средний коэффициент поглощения в малом интервале частот AQ вблизи Q.

Для этого введем величину fi2(), пропорциональную среднему значению Mi2(Q) на интервале ДО

Более подробно см. [70, с. 230; 351, гл, II; 352],

где X и и нумеруют колебательные состояния основного и возбужденного электронного терма;

Р1и - вероятность основного состояния 1х, которая с учетом распределения Больцмана имеет вид:

exp{-E,JkT)

(VII. 7)

- энергии электронно-колебательных состояний; штрихи в суммах по X и и означают, что суммирование по колебательным состояниям проводятся с ограничением:

Последнее может быть снято, если выражение (УП.б) переписать в другом виде с помощью б-функции:

Еп()- Z (>iH\{K\M\2>i}fb{E2, -E-ЬQ) (VII.8)

и, X

с помощью функции Fizi) Ki2(0) записывается просто:

Kl2 (fi) =

4nNQ Зс

f ,2 (Q)

(VII. 9)

Отсюда видно, что функция fi2(fi) определяет зависимость коэффициента поглощения света от частоты и, следовательно, форму кривой поглощения. Fi2(Q) называют функцией формы полосы.

Упрощение выражения для fi2(Q) можно достичь, полагая прежде всего, что электронные термы I и 2, между которыми происходит переход, невырождены и различием частот колебаний в этих двух состояниях можно пренебречь. Тогда соответствующие этим состояниям волновые функции можно представить в адиабатическом приближении в виде произведения электронной части на колебательную (стр. 194)

Ргх = Ч ( 7. Q)X (Q)

где Q - условно обозначает совокупность нормальных координат.

Ограничимся сначала так называемым полуклассическим приближением для случая достаточно высоких температур, когда по принципу соответствия Бора наиболее эффективные колебания с большими квантовыми числами могут рассматриваться приближенно как классические. Тогда конечное колебательное состояние X(Q) является быстро осциллирующей функцией, за исключением так называемых точек поворота, где = 62(Q), т. е. где скорость классического осциллятора равна нулю. В хорошем приближении можно считать, что в рассматриваемом случае эти точки дают основной вклад в интеграл по Q в матричном элементе выражения (VII. 8). Иными словами, в полуклассическом приближении ядра рассматриваются движущимися вдоль поверхности

e(Q). В том же приближении можно написать аналогичное выражение для основного состояния, Ei = Bi(Q).

Подставляя эти выражения в (VII. 8) и учитывая соотношение для колебательных функций

Zocx(Q)ocx(Q) = fi(Q-Q) (VII. 10)

можно получить [предварительно представив квадрат матричного элемента в (VII. 8) в виде произведения двух одинаковых интегралов, по Q и по Q]:

f,2 (Q) =\dQ\ М%(Q)PPi (Q)в (Q)-(VII.П)

(Q) = JF*(<7.Q) М2(Ч Q)dr

Ae(Q) = Pi(Q)=-e

e2(Q)-e,(Q) e, (Q) e,(Q)

l\dQe

(VII. 12) (VII. 13)

(VII. 14)

Формула (VII. 11) есть не что иное, как математическое выражение приближения Франка - Кондона. Согласно последнему предполагается, что за время очень быстрого электронного перехода ядра системы не успевают сместиться, и возбужденное состояние, в которое попадает система после перехода, должно быть взято при конфигурации ядер Q, соответствующей основному состоянию. Поглощаемый при этом квант света fiQ равен разности потенциальных энергий Лб(Р), что обеспечивается 6-функцией.

Для адиабатических потенциалов основного и возбужденного состояний с учетом их сдвига (рис. VII. 1) имеем:

8.(Q) = f/CQ

e2iQ)-

-bQo+-K{Q-Qo)

(VII. 15)

Подстановка этих выражений в (VII. 11) дает

J dQe I Ml, (Q) P б (йо -bQ+-KQ- KQQo) [ dQe

(VII. 16)

В случае, когда рассматриваемый переход разрешен как чисто

электронный, зависимостью Mi2 от Q можно пренебречь. Используя далее интегральное представление б-функции

можно легко вычислить интегралы в (VII. 16).