Ке(0 1,0 KB(Ai)

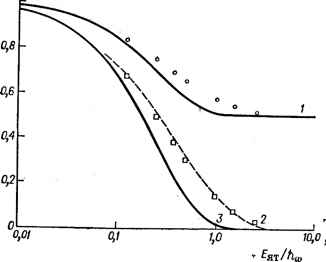Рис. VI. 18. Факторы вибронной редукции (подавления) /С (Е) ( г) линейной Е - е-задаче как функция отношения

Erjbm [282].

t-KE{Ei=4, (1+ехр (-4£ят/Аь>); (Л2)=ехр [-1,974(%т/йи)

3-iC£ (j)=exp (-4Еят/Ао,). Точки соответствуют точным численным значениям; прерывистая линия выбрана совпадающей с последними в области йЛ SEjjhaZ.u.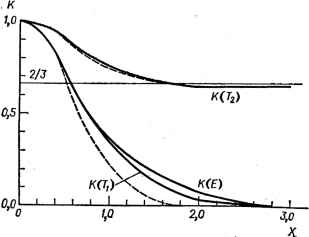

Рис. VI.19. Факторы вибронной редукции для линейной Т - <2-задачи как функции параметра X = [3£ят/ *й]% полученные по данным численного решения [296].

Прерывистые линии соответствуют приближенным значениям по формулам (VI. 94) 1282].

Необходимо отметить, что представления о подавлении теряют описанную выше простоту и привлекательность как только физическая величина перестает определяться только основным состоянием. В частности, при сильном внбронном взаимодействии к основному вибронному мультиплету близко подходит следующий уровень туннельного расщепления (рис. VI. 14 и VI. 15), так что при определении физических величин очень часто приходится учитывать его существенное влияние.

В случаях, когда /С(Г)-С 1, оказывается также существенным учет поправок второго порядка теории возмущения на базисе вибронных функций исходного электронного мультиплета [282].

Обсуждая использование факторов подавления для расчета физических наблюдаемых величин, следует еще раз подчеркнуть, что они сохраняют смысл только для операторов, не зависящих от ядерных координат. Например, если электронный оператор вычисляется во втором порядке теории возмущений, в котором учитываются возбужденные электронные состояния (например, при расчете зеемановского расщепления f-терма октаэдрических систем), то он с учетом вибронного взаимодействия оказывается, вообще говоря, зависящим от ядерных координат и, следовательно, приве-денные соотношения для параметров подавления становятся неприменимыми [313].

Инверсионное расщепление и подавление в спектрах ЭПР*

В качестве примера проявлений эффекта Яна - Теллера в наблюдаемых свойствах молекулярных систем рассмотрим здесь некоторые общие черты ЭПР спектров электронно-вырожденных систем. Этот вопрос особенно важен, поскольку орбитальное вырождение почти всегда связано с наличием неспаренных электронов и, следовательно, отличным отнуля спином, что лучше всего проявляется в спектрах ЭПР.

Эффекту Яна -Теллера в ЭПР посвящено большое число работ, исчисляющихся в настоящее время сотнями (см. обзоры [282, 325-328] и соответствующие главы в монографиях [321, гл. 21; 267, глава III). Поясним наиболее отчетливое проявление эффекта на примере систем, обладающих инверсионным (туннельным) расщеплением (раздел VI.4). Сильное влияние последнего на спектры ЭПР связано, прежде всего, с тем, что вместо одного спинового мультиплета при наличии инверсионного расщепления в системе имеется несколько близких мультиплетов, соответствующих различным инверсионным (электронно-колебательным) состояниям. Взаимодействуя между собой во внешнем постоянном магнитном поле, эти состояния приводят к сложному ходу уров-

* Методы магнитной восприимчивости см. [9 гл. VI; 314-316]; магнитно-резонансные методы и их связь с электронным строением см. [9, гл. VI; 317-321]; Эффект Мёссбауэра и гамма-резонансные спектры см. [9, с, 173; 322-324].

ней, и большему, чем обычно, числу магнитно-дипольных переходов с сильной зависимостью вероятности последних от соотношения частоты резонанса йсо и инверсионного расщепления б.

В качестве примера рассмотрим первый исследованный теоретический случай -херма [329]. Здесь при отсутствии внешнего поля имеются шесть инверсионных состояний, дублет Е ниже и синглет А выше на расстоянии 6 от дублета, причем каждое из этих состояний является дублетом по спину S = /г. По формулам волновых функций инверсионных состояний (VI. 71) нетрудно вычислить магнитный момент в такой системе с учетом орбитальной составляющей через спин-орбитальное взаимодействие с возбужденным орбитальным триплетом Гг, находящимся на расстоянии А, и затем рассчитать поведение уровней системы в магнитном поле. Для октаэдрического комплекса при направлении постоянного магнитного поля вдоль оси 4-го порядка (например, оси Oz) значения энергий шести уровней в магнитном поле даются выражениями [329]

*-i *0-l)p -H(4p)+ S-H

(VI. 96)

где б - Инверсионное расщепление.

Расчеты волновых функций этих состояний и вероятностей переходов между ними позволяют сравнительно легко получить ожидаемый спектр ЭПР в рассматриваемом случае [276]. Анализ этого спектра удобно провести, разбив область изменений магнитного поля Я на три части (рис. VI. 20): / - низкочастотная область,

при которой -РЯ б; Я - промежуточная, -!-рЯ-б; Я/ -

высокочастотная, для которой рЯ б. В низкочастотной области / разрешены с обычной интенсивностью три перехода, указанные на рис. VI. 20 стрелками. Их частоты могут быть описаны в терминах спин-гамильтониана и g-факторов, которые при

рЯ С б для случая Я, < О равны

gi=2-x(6 + 3v); g2 = 2-(2-3Y); gs2- (VI.97)

где Y - интеграл перекрывания колебательных функций различных минимумов - дается формулами (VI. 78) -(VI. 80) и ввиду его малости может быть в ряде случаев опущен.

В другом предельном случае рЯ > б и в высокочастотной области Я/ разрешены другие три перехода с g-факторами:

g2.3 = 2-(2±3v)

(VI. 98)

В промежуточной области II с уменьшением напряженности поля низкочастотный спектр усиливается, а высокочастотный ослабляется, так что при некоторых значениях Я должны наблюдаться и те и другие линии.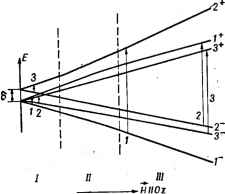

Рис. VI. 20. Уровни энергии основного состояния терма в магнитном поле с учетом инверсионного расщепления.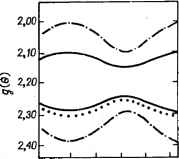

-20 О 20 АО 60 ВО В

Рис. VI. 21. Угловая зависимость g-фактора без учета (пунктирные линии) и с учетом (сплошные линии) инверсионного расщепления. Точками нанесены экспериментальные данные [332].

->

В промежуточных направлениях поля Я, не совпадающих с тетрагональными осями, уровни сближаются таким образом, что различия в g-факторах уменьшаются, и при направлении поля вдоль тригональной оси все значения g-факторов как низкочастотного, так и высокочастотного нолей совпадают и равны g = = 2 - 4VA. Если обозначить направляющие косинусы направления Я через I, т и п, то для угловой зависимости g\ и g2 в низкочастотной области / можно получить (в первом приближении по VA) [330]

gi. 2 = 2 - ± [1 - 3 {Im + Рп + тп )] (VI. 99)

а g3 полностью изотропен. Заметим, что без учета инверсионного расщепления угловая зависимость g-фактора в рассматриваемом случае была бы существенно иной [331]:

= 2 - ± [1 - 3 {Рт + Рп + тп)]!

(VI. 100) 239

На рис. VI. 21 представлены эти две зависимости с учетом и без учета туннельного расщепления и нанесенные точками экспериментальные данные, полученные Кофманом [332, 333] для случая Си* в MgO при 1,2 К (см. также [334, 335]). Опытные данные подтверждают наличие инверсионного расщепления.

Другой яркой иллюстрацией влияния инверсионного расщепления на спектр ЭПР служит температурная зависимость последнего. Оно проявляется через температурную зависимость величины инверсионного расщепления б. Действительно, предполагая сильный рост б с температурой, мы приходим к следующей картине температурной зависимости спектра. При низких температурах б мало, так что при достаточно большом Я выполняется неравенство

б С -д- РЯ и реализуется высокочастотный спектр. С ростом температуры б увеличивается, так что при некоторых температурах (при постоянном Я) б становится --д- рЯ; в результате достигается промежуточная область II. И, наконец, при достаточно вы-

I Я I

соких температурах б -д- РЯ и спектр ЭПР становится низкочастотным, соответствующим области /.

Таким образом, с ростом температуры в некоторой области может быть достигнут переход из высокочастотного спектра к низкочастотному через промежуточную область. Именно такой температурный переход в спектре ЭПР наблюдается для отдельных координационных систем (подробнее см. в работе [9, табл. VI. 4]), число которых увеличивается.

При очень больших туннельных расщеплениях б, когда заселен только нижний вибронный дублет (в случае Е-терма) или триплет (в случае Г-терма), задача ЭПР легко решается с помощью параметров подавления (раздел VI.5). Для частот ЭПР переходов в вибронном дублете Ё-терма можно получить [282] (v - квантовое число сверхтонкого расщепления)

Ьа>+ = (§,РЯ -Ь P,v) ± 1<:(Е) (зРЯ -Ь Р\) [1-3 + Рп + тп)р

(VI. 101)

Туннелирование существенно сказывается и па вероятностях релаксационных переходов [337-339], проявляющихся, например, в ширинах линий ЭПР. Этот эффект связан, во-первых, с наличием нескольких (вместо двух в отсутствие туннелирования) близких уровней, что увеличивают число каналов релаксации. Во-вторых, релаксационные переходы между различными орбитальными состояниями значительно более вероятны, чем между различными спиновыми (или, как говорят, крамерсово сопряженными) состояниями. Первое из этих обстоятельств приводит к тому, что вероятности релаксации в зависимости от соотношения между параметрами могут быть пропорциональны не только первой (прямые процессы) и седьмой (рамановские процессы) степеням температуры, но зависеть от темпер)атуры как ехр(-б/Г) или Г соответственно. Второе из указанных выше обстоятельств приводит к значительному увеличению вероятностей релаксационных переходов.

В ряде работ исследовано также влияние туннельного расщепления: на спектры ЭПР Гг-терма [282, 310], Е- и Гг-тсрмов [340]; на сверхтонкую структуру рассмотренного выше спектра ЭПР 2£-терма [341]; на возможность осуществления медленно насыщаемого микроволнового лазера с широким динaмичecкм диапазоном [342]; на микроволновое поглощение в отсутствие магнитного поля [343]; на резонансное поглощение ультразвука [327, 344]; на аномалии в теплоемкости и теплопроводности [345]; на мёссбауэров-ские спектры [346, 347] (см. также [282-284, 326-328]). Другие проявления эффекта Яна - Теллера см. в главах VII-IX.

4Я 4Я п п

-д- §2=--Р\ и Рг -константы контактного

где g, = 2-

и диполь-дипольного сверхтонкого взаимодействия. Приведенные выше формулы (VI. 97) -(VI. 99) получаются из (VI. 101) для случая сильной вибронной связи, при которой параметр подавления Ке(Е)с/2 (раздел VI. 5). Как показали Хэм [311] и Чейз [336], достаточно сильное влияние случайных деформаций, обязанных дефектной структуре кристалла, приводит в спектре ЭПР лишь к изменению формы линий поглощения (но не к смещениям их положений). Аналогично (VI. 101) получены формулы для частот линий ЭПР в случае вибронного триплета [282].