йоля, ибо оно зависит от состояния остальных электронов, которые, в свою очередь, определяются состоянием данного. Математическое рассмотрение этой ситуации (см. раздел II. 2) приводит к системе нелинейных интегродифференциальных уравнений (11.41), которые решаются совместно посредством метода итерации. Последний сводится к процедуре, в которой при решении уравнения,для данного электрона состояния остальных считаются известными (например, водородоподобными). Полученное решение затем используют для уточнения состояния остальных электронов и создаваемого ими эффективного поля. После этого уравнение для данного электрона решается снова и т. д. до тех пор, пока полученное решение в пределах требуемой точности не совпадает с предыдущим; такое решение называется самосогласованным.

Метод Хартри - Фока дает наиболее точные результаты, совместимые с полным разделением переменных. По этой причине он может служить эталоном верхнего предела точности, достигаемой при таком полном разделении переменных. Значение энергии легких атомов удается вычислить этим методом с точностью до 1-2%. Для молекул задача существенно усложняется многоцентровостью одноэлектронных функций (см. ниже) и поэтому достижение такой точности для них почти невозможно. Все другие методы разделения переменных в рамках этого приближения менее точны, чем метод Хартри - Фока.

Основные принципиальные недостатки метода самосогласованного поля в том, что в нем учитывается взаимодействие между электронами лишь в среднем (т. е. не учитывается явный вид членов l/rjj - так называемая корреляция электронов). Это приводит к существенным отклонениям волновой функции от истинной в точках столкновения электронов, что сказывается на ее поведении в ряде областей, например, вблизи ядра (хотя в среднем -для энергии-она может давать хорошее приближение). Последнее существенно при расчете физических и химических характеристик системы, которые в большинстве случаев зависят от локальных значений функции, а не от их значений в среднем. Учет корреляции электронов поэтому становится сейчас важной проблемой *.

Приближение ЛКАО

Для молекулярной системы нахождение одноэлектронных функций резко усложняется по сравнению с атомом. Действительно, атом, являясь, одноцентровой системой, имеет сферическую симметрию, благодаря которой угловая часть волновой функции электрона легко отделяется и находится непосредственно в аналитическом виде (раздел II. 1). Радиальная же часть подчиняется достаточно простому уравнению [точнее, системе типа (11.41)]. Моле-

* в настоящее время известны различные методы частичного (прямого или косвенного) учета корреляции: наложение конфигураций [34]; нецолное разделение переменных [35]; адиабатическое приближение [36], н др. (см. обзоры [37-39]).

кула из-за наличия многих ядер (неподвижных в адиабатическом приближении) является многоцентровой системой и по своей симметрии в общем случае не допускает дальнейшего ра.зделения трех переменных электрона. Численное интегрирование же системы (11.41) относительно функции трех переменных -практически невыполнимая задача. Отсюда вытекает необходимость дальнейших упрощений.

В подобных случаях обычно прибегают к спасительным разложениям искомой функции по системе известных функций. Если последняя является полной (в математическом смысле этого слова), то такое разложение будет точным. Упрощение здесь сводится к тому, что система функций, по которой ведется разложение, берется конечной, неполной. Такую систему удобнее всего взять в виде набора атомных функций if, всех атомов, входящих в состав соединения (подробно см. главу V). Тогда искомая функция одно-электронного молекулярного состояния - молекулярная орбиталь (МО)-представляется в виде линейной комбинации атомных орбиталей (ЛКАО):

Коэффициенты ЛКАО Cji находят из условия минимума энергии системы, вычисленной при помощи функций W} всех заполненных МО.

Таким образом, в приближении ЛКАО к неточностям одно-электронного приближения прибавляются ошибки, происходящие от разложения искомой функции по неполной системе атомных функций. Различные усовершенствования этого приближения направлены на компенсацию этих ошибок.

Метод МО ЛКАО в настоящее время является наиболее распространенным при исследовании электронного строения молекулярных систем,. а в случае координационных соединений - и наиболее точным (из практически приемлемых). К валентным соединениям (к которым относятся главным образом органические, раздел 1.2) наряду с методом МО ЛКАО весьма применим конкурирующий с ним метод Гайтлера - Лондона (метод валентных связей, локализованных пар). В новой более совершенной форме этот метод получен в виде естественного развития метода МО ЛКАО Ленард-Джонсоном с сотрудниками [20, 21; 22, с. 240] и носит название метода эквивалентных орбиталей. Ввиду малой эффективности этого направления исследования для координационных соединений он не рассматривается здесь подробно.

ГЛАВА II

АТОМНЫЕ СОСТОЯНИЯ

Дается краткая характеристика атомных состояний, которые необходимы для описания электронного строения многоатомных систем, в том числе координационных *.

1М. ОДНОЭЛЕКТРОННЫЕ СОСТОЯНИЯ Угловые и радиальные функции

Определение одноэлектронных состояний многоэлектронного атома основано на предположении о сферической симметрии поля, в котором движется электрон. В этом случае координатная часть его волновой функции может быть представлена произведением радиальной R{r) и угловой ф) составляющих и охарактеризована теми же квантовыми числами п, I, т, что и у водородоподоб ного атома:

Р гт (г, Ь, (р) = R t (г) Yi (О, ф) (II. 1)

Шаровая функция Yim{b,(f) известна непосредственно а Р? {х) - присоединенный полином Лежандра:

(II. 2)

(П.З)

При / = О, m = О (s-состояния) функция (П. 2) не зависит от углов и ф, т. е. функция (П. 1) зависит только от расстояния до центра атома г, так что ее диаграмма в пространстве имеет форму шара (рис. П. 1,а).

При /= 1 (р-состояния) m = О, ±1, т. е. имеется всего три функции (II. 2), две из которых (при m = 1 и m = -1) комплексны. Поскольку в этом случае значения энергии всех трех состояний одинаковы (случай трехкратного вырождения) в качестве волновых функций р-состояний можно взять любые три комбинации функций (II. 1). В частности, удобно их выбрать так, чтобы они были действительными (табл. II. 1, рис. II. 1,6).

* Подробно см. [29, гл. X; 33, гл. I. III; 40, гл. I, II].

Аналогично, действительные комбинации функции (II. 1) можно выбрать для пяти d-состояний (1 = 2; m = О, ±1, ±2) (табл. II. 1, рис. II. \,в,г).

.,л- у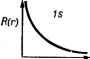

5-0р5италь И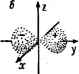

%

р-ОрЫтапь ♦! р-Ор!италь

dj;j-Op too/lb dxi-Орбиталь

кг-Орбиталь й

-%У й-ОрВипаль

dx.yt-Орбиталь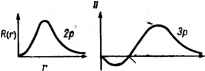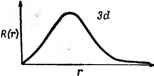

Узел

Рис. II. 1. Угловое (/) и радиальное ( ) распределение атомных функций [41]. as; б-р; в-й{1); e-de).

Отметим, что изображение р и d-состояний на диаграммах стало возможным лишь после произвольного в сущности выбора таких линейных комбинаций [функций (II. 2)], которые действительны и допускают наглядное изображение. Отсюда видна условность гантельного изображения одноэлектронных р-, d- и f-состояний в отсутствие внешних возмущений (при наличии

Таблица И. 1

Одноэлектронные действительные и ортонормироваиные угловые чвсти s-, р- и <{-функций

Обозначение

Функция

в полярных координатах

в декартовых координатах

. Ру

dxy dyz

(3C0S2©-I)

aJsin & cos e cos Ф

sin & cos & sin Ф

V V V

15 1

4Я r 11 1

вырождения утверждение о реализации одного определенного состояния из этих нескольких возможных лишено смысла).

В частности, для семи /-функций (/ = 3; m = О, ±1, ±2, ±3) обычно применяют два набора действительных угловых частей (табл. II. 2, рис. II. 2). Первый из них, называемый кубическим, удобен при исследовании поведения системы в кубическом окружении лигандов (см. стр. 100). Второй набор предпочтителен при более низкой симметрии окружения. В то же время функции одного набора легко получаются в виде простой линейной комбинации функций другого набора (например, fy, = - {li)X

X[VT0f 3 , + V6/J)-

Радиальные функции Rni{r) в (II. 1) для одноэлектронного во-дородоподобного атома могут быть также представлены в аналитическом виде (Z -заряд ядра, Со - боровский радиус)

Таблица п. 2

Одноалектронные действительные и ортонормироваиные угловые части атомных /-функций

Обозняче-нне

Функция

в полярных координатах

в декартовых координатах

У fxyz

fx (Z=-J/ )

fz (x-z )

Кубический набор

105 16я

Ш 16я

(5 sin & cos ф - 3)

sin в sin ф

(5 sin2 0sin2ф -3)

Л/ХШ (ScosO-Scos))

V V

sin Ь COS Ь sin 2ф

sin О cos ф (cos* Ь -

- sin2 е sin2 ф)

8!п©МПф(С08=д- .

- 81п=Фс082ф)

sin & COS & COS 2ф

л/ ш

Vis-

V105 ш

Низ к о с имметричный наб

-;с(5*-3г)

-1г(52-3г) I

-рз-хуг

-z(*-j,) op

z(5z-3r)

-~x{5z-r)

-f/(5z-r=) 1

-2(>:-f,)

±jc(x-3y)

-y(3x-y )