Таким образом, можно получить:

(VI. 76)

где для вытянутого октаэдра Q = ро дается формулой (VI. 32), а для сплюснутого Q = -ро.

Вид электронных волновых функций в минимумах можно найти непосредственно, подставляя в общие формулы (VI. 36) и (VI. 37) значения й, соответствующие координатам минимума. Таким образом, например, для удлиненного октаэдра получаем:

<p, = lt,; <pj, = -.,I --g; <рз = 1 (VI.77)

Для интеграла перекрывания имеем:

S = J <Pi<P2 dx J х, Х2и dX-jy

a=l a=l a=l

(VI. 78)

Пренебрегая выщеуказанным расщеплением eg-частоты в минимумах, можно получить для основного колебательного состояния Шз = Шз = О

2ft

/ 1 Vr V

где Еят определяется по формуле (VI. 34).

Аналогично вычисляется Ук для возбужденных колебательных состояний.

С учетом расщепления частот в минимумах на две компоненты сор и Шф получаем (р = соф/сор):

Vo =

( бр у/ Чзр= + 10р-ьз/

P=-f 3 1

tOp 3p2-i-l0 + 3.

(VI, 80)

Для вычисления йедИагональнйго матричного элемента гамильтониана

+ 2 ZCaQaaQpX SP

(VI.8I)

положим для определенности Л > О и Л > 0. Тогда с учетом значений функций ф{ по (VI. 77) и гармонических осцилляторов X (Qa*) с координатами QJ/* по (VI. 76), а также матричных

элементов операторов {dVjdQQ и {dVIdQadQ по секулярному уравнению (VI. 28), можно получить для основного состояния и р = 1:

Uo---Ш-л/ AQ + 2 V3 AQQi х.) ==

= 4 Л 4 QOVO - V3- Л 4 Qc., = 4 (, )vc (V1.82)

Из этой формулы, в частности, видно, что, так как t/ > О, то, как и ранее, основным инверсионным состоянием будет дублет (рис. VI. 15). Пренебрегая значением по сравнению с единицей, можно записать:

*о=Уо(ят-4-Д)

(VI. 83)

Отсюда естественно следует, что для основного состояния Е-е-задачи критерии приближения туннельных расщеплений хорошо выполняется уже при Еят йсо. Волновые функции инверсионных уровней А и Е определяются по формуле (VI. 71) с коэффициентами по табл. VI. 3.

Полученные выражения для энергий и волновых функций инверсионных (туннельных) уровней в указанном приближении не совсем точны, так как в выражениях (VI. 77) не учитывается сильная зависимость электронных состояний в минимумах от ядерных координат [ср. с (VI. 36)]. Впоследствии задачу решали и другими методами. Например, ОБрайен [306], в отличие от приведенного рассмотрения, отталкивалась от линейного случая мексиканской шляпы с достаточно глубоким желобом, для которого приближенное решение (в области вблизи дна желоба) получается непосредственно

(г,Р,Ф) = 1)(г,<р); (р-Ро)е (/п=±1, ±...-) (VI.84)

fico.

где / (р)-осцилляторные функции.

(я = 0, 1,...) (VI.83)

Включая теперь квадратичные члены вибронного взаимодействия в виде возмущения и считая, что они не перемешивают колебательные состояния с разными п, можно получить следующее

приближенное уравнение для движения вдоль желоба

-5 -Ь р cos Зф - £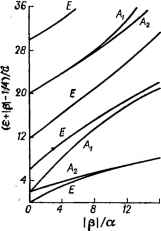

Х(Ф) = 0 (VI. 86)

(Йсор)

ЗМр;

Рис. VI. 17. Вибронные уровни энергии квадратичной Е - е-задачи как функция отношения I р /а, полученные решением уравнения (VI. 86) (по работе [306]).

Результаты численного решения этого уравнения приведены на рис. VI. 17. Можно видеть, что уже при ( р /а) 2, т. е. когда величина квадратичного барьера становится больше кинетической энергии свободного движения в желобе, 16 качественная картина расположения низ-колежащих уровней соответствует ожидаемому в теории инверсионного (туннельного) расщепления.

Рассмотрение ОБрайен [306] нельзя признать достаточно корректным, так как по численным оценкам, приведенным в этой же работе, в рассматриваемом случае сильной вибронной связи р сравнимо или больше колебательного кванта йсор, и, следовательно, пренебрежение перемешиванием колебательных состояний и разделение движений по р и ф необосновано (к тому же в [306] волновые функции инверсионных состояний не получаются в удобном для использования виде).

Недавно [285] предложено использовать вариационный принцип для решения этой задачи. Можно показать, что пробные функции вида

Хе (р. ф) - { } ехр [- J (<7 - 1 ) -f V cos Зф] (VI. 87)

где Л -константа нормировки; q = р/ро [и аналогичная функция для Л-уровня с множителем со8(Зф/2)], с двумя вариационными параметрами ы и v удовлетворяют всем требованиям симметрии и поведения функции вблизи минимумов и под барьерами между ними. Минимизация полной энергии, вычисленной с помощью этих функций, позволяет определить значения энергий уровней и параметров ы и V как функций параметров линейного Х = 2£ят/йюр и квадратичного у = 2A/fic)p барьеров.

В более сложном случае Г-терма туннельное расщепление для частных случаев линейных Г-<2- и Г-е-задач определяется относительно не сложно. В Г-случае с четырьмя тригональными

минимумами адиабатического потенциала матричный элемент вычисляется аналогично случаю Е-терма с надлежащим набором нормальных координат типа tz в минимумах [276, 302]. В линейном приближении получаем

причем для основного колебательного состояния:

у = ехр(-44т/ЗН)

(VI. 88)

(VI. 89)

Более точные расчеты для этого случая, упомянутые нами выше, приводят к системе уровней рис. VI. 14.

В случае линейной Г-е-задачи электронные функции, как указывалось в разделе VI. 3 ортогональны между собой. Поэтому 1/=0 - основное триплетное состояние не расщепляется тунне-лированием (что непосредственно следует также из соображений симметрии).

Решение для общего случая Г -(е +г)-задачи встречает большие трудности, связанные со сложным характером полученного выше пятимерного адиабатического потенциала. Расчеты для некоторых низколежащих уровней энергии в линейном приближении проводились при ограничивающих предположениях о характере вибронной связи с двумя типами колебаний. Сильная связь с е-и <2-колебаниями рассмотрена ОБрайен [307]; исследованию любой произвольной связи с этими колебаниями в предположении

= соь и Еят = -Еят посвящены работы [307, 308], а сильная связь с е-колебаниями и слабая связь с 2-колебаниями рассмотрена в статье [309].

Туннельное расщепление в случае шести орторомбических минимумов адиабатического потенциала, обязанных влиянию квадратичных членов в основном состоянии приводит к двум виброн-ным триплетам типа Ti и Гг [280, 281] с расщеплением

3 рс

24 - 28ЛГ - + 9N S

S = exp

(4 - 3N) (4 - 3/у2) 12 - 20ЛГ -

3 £Т

L 2 Йсо (4-3N){4

l-S - дМ) J

(VI. 90)

(VI. 91)

где константа определяется по (VI. 54).

Подавление электронных величин вибронным взаимодействием

Одно из интересных следствий вибронных взаимодействий - уменьшение (подавление) физических величин, определяемых электронным строением основного состояния. Речь идет об обратном влиянии динамики движения ядер, полученной с учетом вибронного взаимодействия, на электронное строение и его характеристики.

Выше при решении вибронной задачи подчеркивалось, что основное вибронное состояние во всех случаях получается того же типа симметрии (той же мультиплетности, степени вырождения и т. д.), что и исходный электронный терм в максимально-симметричной конфигурации ядер. Этот результат можно объяснить тем, что члены вибронного взаимодействия V по (VI. 18), возмущающие электронные состояния, в совокупности имеют ту же симметрию, что и основной гамильтониан, и поэтому они не снимают вырождения электронного терма (вопреки упрощенной формулировки теоремы Яна -Теллера, см. раздел VI. 2).

Совпадение типа симметрии терма основного состояния с учетом и без учета вибронного взаимодействия позволяет в ряде случаев существенно упростить расчеты наблюдаемых величин. Еще в первой работе по расчету спин-орбитальногб расщепления основного вибронного уровня [310] было показано, что без учета перемешивания с другими уровнями это расщепление пропорционально не только константе спин-орбитальной освязи, как в случае расщепления чисто электронного терма, а той же константе, умноженной на интеграл перекрывания колебательных функций в соседних минимумах Уи по (VI. 78). Так как Уи < U то это расщепление в результате учета влияния вибронного взаимодействия оказывается значительно уменьшенным, иногда на несколько по- рядков. Хэм [282, 311] обобщил эту идею и показал, что так подавляются любые физические величины, если их операторы зависят только от электронных координат.

Можно сформулировать следующую теорему о подавлении: пусть необходимо вычислить матричный элемент оператора физической величины -/гу (О. преобразующейся по строке у неприводимого представления Г точечной группы симметрии задачи, на функциях основного вибронного состояния 4rv(r,Q),H пусть известны волновые функции исходного электронного терма фгу()-. Теорема подавления утверждает, что

\ Ргусгу Сг) Prv. dxKrif) *rv,%v*rv. dx (VI. 92)

где /Сг(Г)-константа, не зависящая от конкретного вида оператора F, а только от типа симметрии Г, по которому он преобразуется, и от вибронных параметров. Доказательство этой теоремы см. в работах [267, 309]. /Сг(Г) называют константами подавления (или редукции).

Из теоремы подавления следует, что если только константы Кт(Т) известны, то для определения электронных характеристик основного состояния системы нет необходимости решать виброн-ную задачу - достаточно вычислять матричные элементы на исходных электронных функциях вырожденного терма. В частности, можно определить константы /Сг(Г) из одного эксперимента и использовать их для предсказания результатов во всех других.

при решении вибронной задачи можно получить и выражения для констант подавления через константы вибронной связи. Для линейной £-е-задачи получаются значения /СвИг) и Ке{Е), приведенные на рис. VI. 18. Для линейной Г-е-задачи можно приближенно принять [282, 311]:

(Г,) (Т) - ехр (- 3£°т/2Ё ),) Kj{E)=\

(VI. 93)

Более точные значения этих констант с учетом влияния колебаний получены численно [307, 309]. Для случая линейной Г-<2-задачи известны следующие приближенные выражения [282]

Kj.(7,) Кг{Е)с ехр (- 94т/4й ,) (2) i [2 + Р (- 9£ят/4ЙС0б)

(VI. 94)

которые качественно согласуются с результатами численного расчета [296] (рис. VI. 19).

Для случая орторомбических минимумов при Ка = Кь= К (й = (06 = (О имеем [280, 281]

/Су (£) = (Ц-8S-Ь 6S) (4-f 8S)-

Kj{T) = {3S + S)(\ -b2S) /Cr(72)=(l+6S)(2-t-4S) К

S=l ехр(-7С(3<>7йсо)

(VI. 95)

где координаты точки минимума Qf°> даются выражениями (VI. 55).

Из приведенных формул видно, что подавление электронных характеристик, обязанное вибронному взаимодействию, экспоненциально зависит от отношения £ят/Ёсо, определяющего величину эффекта Яна - Теллера, и поэтому в случае сильной вибронной связи весьма велико. В частности, во всех случаях сильнее всего подавляются операторы типа Т\, к которым принадлежит орбитальный момент электронов и, следовательно, спин-орбитальное взаимодействие. Существенное подавление спин-орбитального расщепления основного состояния (иногда на 1-2 порядка, см. например, [310]) -одно из наиболее ярких проявлений эффекта Яна -Теллера в системах с Т-термом (С-терм не расщепляется спин-орбитальным взаимодействием в первом порядке). Другие подавляемые величины - это, например, анизотропная (орбитальная) часть зеемановского расщепления, все виды взаимодействия электронной оболочки с ядром (диполь-дипольные, квадрупольные и др.), кулоновские и обменные взаимодействия между электронными оболочками ян-теллеровских центров в кристалле [312] и др.