сформулированной прямой задаче. В этих уравнениях предполагается, что электронные состояния при фиксированных ядрах (адиабати- ческие потенциалы) известны и решается задача о поведении ядерной системы. Поэтому решение этих уравнений по физической сущности есть не что иное как решение обратной задачи квантовой химии. Ее можно вкратце сформулировать в тех же терминах, что и прямую задачу: для известного электронного строения молекулярной системы при фиксированных ядрах необходимо определить соответствующее ему поведение ядерной подсистемы *.

В то время как прямая задача квантовой химии решается вот уже скоро полстолетия, обратная задача начала решаться недавно- лет 15 тому назад. Между тем интерес к ней непрерывно возрастает по мере увеличения вычислительных мощностей и возможностей более тонкого экспериментирования. Заметим, что одна из центральных задач химической науки - определение механизмов и скоростей химических реакций - в сущности опирается на решение обратной задачи.

С известными ограничениями (см. стр. 204) эффекты Яна - Теллера и Реннера можно рассматривать как качественные аспекты обратной задачи вблизи точки вырождения или псевдовырождения. Ее более полное выражение дается системой уравнений (VI. 13). Собственные значения этой системы дают уровни энергии системы, а функции %j{Q), будучи подставлены в выра--жение (VI.14), позволяют определить распределение ядерной плотности или вероятности той или иной конфигурации ядер. Дальнейшее обсуждение этой важной задачи дается при анализе приложений (главы VII-X).

Общие решения. Случай слабой вибронной свизи

Полное решение системы вибронных уравнений (VI. 13) весьма сложно и проведено до сих пор только в двух случаях - линейной Е-е-задачи [295] и линейной Г -г-задачи [296]. В первом случае для молекулярной системы с потенциалом вида мексиканской шляпы система (VI. 13) состоит из двух зацепляющихся уравнений. Численное решение последних позволило получить таблицы уровней энергий и коэффициентов волновых функций для различных значений константы линейной вибронной связи, которая в данном случае представлена в виде 7. = 2£ят/йсор, где Йсор - квант колебаний в желобе (вдоль координаты р). С этими данными были вычислены вероятности электронных переходов с участием Е-терма и невырожденного Л-терма: Л-*£ и Е-*А (см, рис. VII. 5).

* По замечанию М. Г. Веселова, приведенные здесь формулировки прямой и обратной задач по сути своей должны быть переставлены местами, так как определение движения ядер больше соответствует прямой задаче решения дифференциального уравнения. Нам представляется, однако, что в методическом отношении приведенная классификация более приемлема.

Для линейной f-/2-задачи в системе (VI. 13) получаются три зацепляющиеся уравнения. Их численное решение позволило получить систему уровней энергии как функцию X, приведенную на рис. VI. 14. Позднее [297] на основе этих данных была также рассчитана форма полос ожидаемого электронного спектра (см. рис. VII. 11).

5,0 г-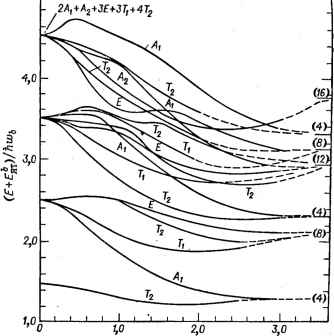

Рис. VI. 14. Вибронные уровни энергии как функция параметра Ejjbah, полученные численным интегрированием вибронных уравнений для линейной Т - /г-задачи [296].

Можно видеть, что эти два случая далеко не исчерпывают обратную задачу квантовой химии, и ввиду сложности решения система (.VI. 13) в общем виде весьма желательны исследования предельных случаев, а также приближенные и полуэмпирические решения.

Прежде *всего, целесообразно разделить задачу на два предельных случая (йо) - квант колебаний в минимуме адиабатического потенциала):

Л < 1 лт < у fiw - слабая вибронная связь Л > 1 Efij > Йт - сильная вибронная связь

в чисто физическом плане принципиальное различие между этими двумя вариантами состоит в том, что в первом из них при

ят < в потенциальных ямах, характеризующих искаженную

конфигурацию системы, могут не реализоваться локальные состояния, в то время как во втором они всегда есть. Однако в обоих вариантах, как мы увидим ниже, в стационарных состояниях система делокализована по всем эквивалентным минимумам. Поэтому используемые иногда названия динамического эффекта Яна - Теллера для случая слабой связи и статического - для сильной - неудачны, ибо оба случая динамические . Термин, статический эффект имеет смысл лищь для обозначения ситуации, когда рассматривается состояние одного минимума, или предельный случай больших барьеров между минимумами, когда состояние в каждом из них практически стационарно.

Рассмотрим сначала приближенные решения для случая слабой связи. Общее исследование показывает [271, 298-300], что в этом случае моменты количества движения электронов и ядер в отдельности не сохраняются, а сохраняется их некоторая сумма. Дополнительное специальное квантовое число, составленное из квантовых чисел проекций моментов количества движения электронов и ядер, характеризует уровни энергии системы в целом. Ситуация здесь несколько аналогична той, которая возникает при сложении орбитального и спинового моментов количества движения при LS-связи в атомах.

Для случая К < 1 уровни энергии системы с учетом вибронного взаимодействия могут быть найдены методами теории возмущений. Для линейной Е-е-задачи невозмущенная задача является двухмерным осциллятором. Во втором приближении теории возмущения для уровней энергии получаются следующие выражения [295, 298, 299]:

Ер1=Ьт[р + 11\--(\1\+У Ер1Ът[р + \1\-1 + (\1\-У

(р = 1,3. 5,...)

(р=2, 4,6,...) (VI.69)

/=±1. ±.

Отсюда видно, что так как энергия зависит только от абсолютного значения /, все уровни энергии (в том числе основной) двукратно вырождены. Следовательно, первоначальное двукратное электронное вырождение не снялось, а трансформировалось из электронного в вибронное.

Для Т-/г-задачи исходное (нулевое) приближение является трехмерным осциллятором, а для возмущенных вибронным взаимодействием уровней энергии получается [299]

£nmi-Eco{n---f (/(Л-1)-т(т-1-1)-6]л} (VI.70)

где п = 0, 1, 2, т = п, п - 2, n - i..... 1 или 0; 1 = т,

mil, при m > 1 и / = 1 при m = 0. Здесь вырождение каждого уровня равно 2/+1, так что для основного состояния п = 0, т = 0 и /=1, 21-\-1=3, т. е. сохраняется трехкратное вырождение исходного Г-терма.

Для остальных, вибронных задач простые формулы типа (VI. 69), (VI. 70) неизвестны.

Случай сильной вибронной связи. Инверсионное (туннельное) расщепление [301-304, 280-284]

В случае сильной вибронной связи К > 1 (ят > <) глубины минимумов адиабатического потенциала достаточно велики, так что в точках минимумов расстояние до следующего листа адиабатического потенциала (равное, например, для С-терма 4£ят), становится сравнимым с обычными расстояниями между потенциалами невырожденных термов. Тогда, в области вблизи минимумов система уравнений (VI. 13) расцепляется и для них становится применимым обычное адиабатическое приближение для невырожденных термов.

Предположим, что в нулевом приближении состояния в минимумах независимы; обозначим электронную функцию в i-м минимуме посредством ф{, колебательную х, и полную Q)i = (ргХы-Так как в системе г эквивалентных минимумов, то в этом приближении система г-кратно вырождена. Можно легко установить, какими членами гамильтониана необходимо пренебречь, чтобы получить решение Фи- Считая эти члены малым возмущением, запишем полную волновую функцию нулевого приближения в виде линейной комбинации:

Чаи=ЕСгаФ/и (а=1.2.....г)

(VI. 71)

Тогда уровниг энергии и коэффициенты Ci определяются из решения секулярного уравнения

[l;-£ S l = 0 (/,/ = 1...., г) (VI.72)

где Н - полный гамильтониан, а 55= Ф/иФ/и dx - интеграл перекрывания.

Можно легко показать, что для/=?*:/Я?/ = Я 2==Г/и, Sy = S2= = Sk, и уравнение (VI. 71) решается непосредственно. Полученные Еа и для г = 3, 4, 6 цривсдены в табл. VI. 3. Видно, что если Vy ф О, то рассматриваемый и-ый электронно-колебательный уровень в минимуме расщепляется на два (рис. VI. 15): один невырожденный и один двукратный (в случае г 3) или трехкратный (для г = 4), либо два трехкратных (г = 6) (см. также [290]). По аналогии с аммиаком это расщепление было названо

Симметрия инверсионных уровней

Энергии уровней

Коэффициенты

1 -S 1+25

l-S 1-3S

1 +2S

2<7к 1 -2S

V6(l-S) 1

(0, I, -1)

V2(l -S)

2V1 -s 1

2V1 -S 1

2Vl -S I

2 Vl + 3S 1

2VI +2S 1

2 Vl + 2S

2 Vl + 2S 1

2 Vl - 2S 1

2 Vl - 2S 1

2VI -2S

(l.-l. -1, 1) (l.-l, 1, -1) (1. 1, -I, -1) - (1. 1. 1, 1)

(1, 1. 1. 1. 0, 0) (1. 0, -1, 0, 1, 1) (0, -1, 0, 1, 1, -1) (1, -1, 1, -1, 0, 0) (-1. 0, 1, 0, 1, 1) (0, -1, 0. 1, -1, 1)

инверсионным [302]; некоторые авторы считают более удобным название туннельное расщепление (см. [267, 282]). Критерием применимости теории возмущений является малость инверсионного расщепления по сравнению с величиной колебательного кванта в минимуме Ёсо:

. 6и<Ёсо (VI. 73)-

Для вычисления обратимся сначала -к Е-е-задаче. Для этого случая в соответствии с табл. VI. 3 имеем:

, зи

1 + 2Sk 1 - S (1 + 2S ) (1 - SJ

(VI. 74)

Отсюда видно, что для расчета б необходимо вычислить и и. Для этого необходимо задаться определенным видом колебательной функции в минимумах х/и- В принятом предположении

dlkj

Рис. VI. 15. Инверсионное (туннельное) расщепление в квадратичной Е - е-задаче (а), линейной Т - <2-задаче (б) и в орторомбиче-ских- минимумах квадратичной Т - {е + <2)-задачи (в).

достаточно глубоких минимумов естественно считать нормальные колебания гармоническими (по крайней мере для достаточно низких колебательных состояний и). Поэтому можно записать

XiK = nXm (QaO (VI. 75)

а=1

где % (Qa О ~~ гармоническая ос-

цилляторная функция для Шц-коле-бательного состояния нормального колебания Qa* в i-ой равновесной конфигурации. В последних только тетрагональные eg-типа колебания Qi и Q3 окажутся различными, остальные нормальные колебания не смещены и одинаковы во всех конфигурациях. В тетрагональных минимумах двукратно вырожденное eg - колебания расщепляется на два: aig (типа Q3 см. рис. VI. 1 и табл. VI. 1) и big (типа Q2) (расчеты таких расщеплений см. [305]).

Выражения для новых нормальных координат в минимуме Q2* и Q3 можно найти из соображений симметрии так, чтобы они переходили друг в друга при операциях симметрии системы,

в частности при повороте ее на ± (рис. VI. 16).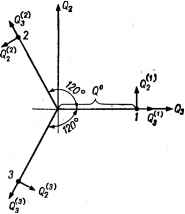

Рис. VI. 16. Выбор местных нормальных координат в каждом из трех тетрагональных минимумов в пространстве е-смещений.

Коэффициенты С, , Са,..., С, (а = 1, 2.....г) из (VI.71),

записанные в виде iV (m , п ,£ ), где iV - иориировочиый множитель