двойной штриховки тригональные экстремумы глубже тетрагональных, а в области одинарной штриховки, наоборот, тетрагональные экстремумы глубже тригональных. Во всех случаях для устойчивости системы необходимо, чтобы M-<; 1.

Наиболее существенно влияние учета квадратичных членов .еХ2-типа на положение и характер шести эквивалентных промежуточных экстремумов орторомбического типа (которые в линейном приближении могут быть только седлообразными точками). Их глубины и координаты одного из них (для остальных

Рис. VI. 10. Область существования абсолютных

бических минимумов адиабатического потенциала Г - (е--<2)-задачи с учетом квадратичных членов.

координаты могут быть найдены из соображений симметрии) даются выражениями:

= в- (;v2 4д2д m)/8KaN (1 - м)

= Л(2- N)l2Kb{l-M) Qf = с (ЛГ - 2M)l2KN (l - М )

(VI. 55)

При пр иближении к точке С = 0, М = Л = 0 вдоль линий Af== = ±yvV3/2Ha плоскости MN (рис. VI. 9) глубина этих экстремумов становится равной глубинам тетрагональных и тригональных: ят =-£ят = £ят. и реализуется упомянутый двумерный желоб минимумов на пятимерной поверхности адиабатического потенциала. Вне этой точки £ят Ф Efir, так что с учетом квадратичных членов вибронного взаимодействия, двумерный желоб минимумов гофрируется , - вдоль желоба появляются чередующиеся холмы и впадины, в принципе вполне аналогичные случаю £-терма. Весьма важно, что для большой области параметров М и N орто-ромбические экстремумы становятся абсолютными минимумами (рис. VI. 10).

Наряду с этими тремя типами экстремумов с учетом квадратичных членов на поверхности адиабатического потенциала появляются три новых типа экстрему.мов, в двух из .которых имеется

по 12 эквивалентных, а в третьем их 24. Однако область существования последнего типа экстремумов выходит за пределы значений параметров, при которых система устойчива, а экстремумы первых двух типов нигде не становятся абсолютными минимумами. Подробные расчеты в этпх случаях проведены численно [281, 289].

Теоретико-групповому исследованию формы потенциальных поверхностей при вибронном взаимодействии посвящены работы [290].

Псевдовырожденные состояния

Рассмотрим сначала простой случай двух близких невырожденных электронных состояний и i))2, разделенных интервалом энергии 2А [274]. Учитывая, как и ранее, линейные члены вибронного взаимодействия V по (VI. 18) в виде возмущения, мы придем к секулярному уравнению (VI. 19), которое для рассматриваемого случая приобретает вид (предполагается, что только одна координата Q перемешивает рассматриваемые состояния)

(VI. 56)

- Д - е aQ aQ Д - е

где а = ()р - константа линейной вибронной связи (энергия

е отсчитывается от середины интервала 2Д).

Решения (VI. 56) -вибронные поправки к электронным энергиям - находятся непосредственно

е = ± + aQ (VI. 57)

что с учетом энергии упругой связи в остове по (VI. 17) (которая для простоты предполагается одинаковой в обоих состояниях) дает: .

е {Q)=~KQ± Va + oV (VI. 58)

Из этого выражения видно, что с учетом вибронного взаимодействия два адиабатических потенциала меняются по-разному: в верхнем кривизна (частота колебаний) увеличивается, а в нижнем-уменьшается, но до тех пор пока А>(а1К) минимумы обоих кривых находятся в точке Q = О (случай слабого псевдоэффекта Яна - Теллера; рис. VI. И, о). При =/СА кривизна нижней кривой становится равной нулю.

При выполнении условия

A<flV/C (VI. 59)

система (в состоянии нижнего листа) становится неустойчивой по отношению к смещениям Q (сильный псевдоэффект Яна - Теллера; рис. VI. 11,6). Минимумы адиабатического потенциала расположены в точках

S (VI. 60)

Рассмотрим теперь более сложный случай комплекса переходного металла с электронной конфигурацией (Р, например, четырехвалентного титана, с октаэдрической координацией кислородного типа [284, 291]. Одноэлектронная схема уровней МО ЛКАО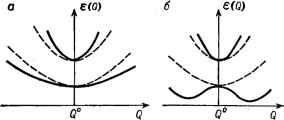

Рис. VI. 11. Поведение адиабатических погенцналов в случае слабого Jja) и сильного (б) псевдоэффектов , Яна - Теллера.

Прерывистыми линиями показаны те же потенциалы, но без учета их вибронного перемешивания.

(раздел V. 3) для этого случая иллюстрируется на риС. VI. 12. Основное состояние системы как целое есть Mig, а ближайшее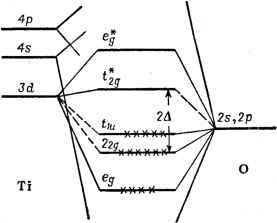

Рис. VI. 12. Примерная схема одноэлектронных уровней энергии МО и их заселенности в кластере TiOg~.

возбужденное состояние той же мультиплетности Tiu соответствует возбуждению одного электрона с 1 -уровня. Для сколь-нибудь полного рассмотрения задачи необходимо принять во внимание образующие эти термы шесть 2/7л-орбиталей кислорода и три Зл-орбиталей титана, комбинации которых формируют ближайшие внешние hg, tiu и молекулярные орбитали комплекса.

Основное Aig и ближайшее возбужденное Ti U состояния комплекса перемешиваются его нечетным трехкратно вырожденным колебанием типа <i (ig X = Tiu). Обозначим его три компоненты через Qx, Qy и Qz (рис. VI. 13) и исследуем поведение адиабатического потенциала системы в пространстве этих координат. Ограничиваясь линейными членами возмущения V по (VI. 18), мы должны ввести в соответствии с теоремой Вигнера - Эккарта (III. 35) одну константу вибронной связи а, через которую можно выразить все матричные элементы секулярного уравнения теории возмущений (VI. 19), построенные на упомянутых выше девяти функциях атомов Ti и О:

=5*Д)с*-н (VI. 61)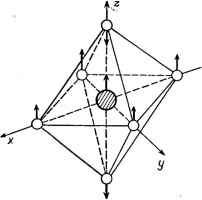

Другой константой будет 2А - энергетическое расстояние Рис. VI. 13. Сг-Компонента нечетного между атомньГми состояниями Гщ - колебания в комплексе TiOg~ 3dxy{Ti) и 2ру{0). Не выписывая (длины стрелок выбраны условно), здесь всего уравнения, приведем сразу его корни - поправки к электронным энергиям, возникающие из-за ядерных смещений:

=5.6-

Заселяя нижайшие три уровня шестью электронами и подставляя соответствующие выражения из (VI. 62) в (VI. 20), мы получим следующее приближенное (из-за пренебрежения межэлектронным отталкиванием) уравнение для адиабатического потенциала основного состояния:

е {Qx. Qy. Qz)=K (Ql + Ql + <Й) -

-fVA + aQ + CD] (VI. 63)

Форма этой пЬверхности зависит от соотношения между константами А, а и /С. При А > {4аУК) поверхность имеет один минимум в точке Qx= Qy = Qz - О, в которой система имеет первоначальную неискаженную конфигурацию. Этот случай соответствует слабому псевдоэффекту Яна -Теллера (рис. VI. 11,с). Но если

(VI.64)

то поверхность (VI. 63) приобретает сложную форму с четырьмя типами экстремальных точек:

один максимум в точке Qx = Qy = Qz = 0 (динамическая неустойчивость) ;

восемь минимумов в точке Qx = Qy = Qz = Qi

0<> = [(8аМ)-(дМ1/ (VI. 65)

на глубине £пят, отсчитанной от точки максимума - энергии стабилизации псевдоэффектом Яна -Теллера

fj.p = 3 [iaK + HKlia - 2Д] (VI. 66)

В этих минимумах атом Ti смещается вдоль тригональной оси, приближаясь одновременно к трем атомам кислорода и отдаляясь от трех других;

двенадцать седлообразных точек при Qp = Qg =И= О, Qr = О, р, q, г = X, у, Z (с максимумом в сечении г и минимумами вдоль р и <7). В этих точках атом Ti смещен к двум кислородам, расположенным на осях р и q;

щесть седлообразных точек при Qp==Qq = 0, Qr = Qo

Q<f) = V(16aW-(AV) (VI. 67)

на глубине

£g).j, = 2 UajK + klW - 2Д] (VI. 68)

Аналогичная трактовка возможна и для тетраэдрических комплексов [292], В этом случае в сильном псевдоэффекте Яна-Теллера ожидаются четыре эквивалентных минимума, в каждом из которых имеется одна неэквивалентная связь ц. а. -лиганд, которая короче или длиннее трех других, остающихся одинаковыми.

Приведенные вьше примеры показывают, что в случае достаточно близких электронных термов (псевдовырождение) адиабатический потенциал имеет особенности, аналогичные полученным выше для случая точного вырождения, а именно: неустойчивость в конфигурации максимальной симметрии и наличие нескольких эквивалентных минимумов. Критерий сильного псевдоэффекта Яна - Теллера (или критерий неустойчивости) (VI. 59) или (VI. 64) (во всех остальных случаях он имеет в принципе тот же вид) содержит три параметра, А, К п а, тл поэтому может оказаться весьма мягким для одного из них. В частности, сильный эффект может возникнуть при больших Д, если К мало или а велико.

Существенны для приложений и те случаи, когда этот критерий не выполняется, т. е. А alK. Действительно, хотя при таком соотношении параметров неустойчивости адиабатического потенциала не возникает, но, как уже указывалось (рис. VI. И, а), в результате вибронного взаимодействия кривая адиабатического потенциала основного состояния становится более пологой, т. е. система размягчается в направлении Q, и тем больше, чем больше а и меньше А в сравнении с К. Это обстоятельство очень

важно, Например, при Исследовании механизмов химических реакций (см. раздел X. 3).

Наряду с большим сходством имеются и существенные различия между эффектом и псевдоэффектом Яна - Теллера.

Отличительной особенностью псевдовырождения является то, что смешиваемые колебаниями электронные состояния Г и Г могут принадлежать к разным представлениям группы симметрии задачи (в то время как в случае вырождения Г = Г). Это обстоятельство существенно меняет пространство нормальных смещений ядер, в котором проявляются неустойчивость системы и сложный характер адиабатического потенциала. В частности, для систем с центром инверсии Г и Г могут обладать противоположной четностью, вследствие чего константа а отлична от нуля только для нечетных ядерных смещений Qu, снимающих центр инверсии и приводящих к образованию дипольного момента (ди-польная неустойчивость [293, 294]). В этом случае в каждом из минимумов адиабатического потенциала система будет обладать дипольным моментом (см. раздел IX. 2). Вполне очевидно, что этот эффект невозможен в случае взаимодействия электронных состояний вырожденного терма, так как в этом случае Г = Г и активные смещения Q могут быть только четными.

VI. 4. РЕШЕНИЕ ВИБРОННЫХ УРАВНЕНИЙ. ИНВЕРСИОННОЕ (YУHHEЛbHOE) РАСЩЕПЛЕНИЕ

Обратная задача квантовой химии

Рассчитанные в предыдущем разделе адиабатические потенциалы электронно-вырожденных и псевдовырожденных систем позволяют, подставив эти потенциалы в вибронные уравнения (VI. 13), перейти к исследованию динамики движения ядер в таких системах. По сути своей такая процедура может быть названа решением обратной задачи, квантовой химии. Действительно, наиболее общей известной до сих пор центральной задачей квантовой химии с момента ее возникновения как науки в 1927 г. было определение электронного строения молекулярной системы, имеющей определенную ядерную конфигурацию (т. е. при фиксированных ядрах). В некоторых случаях конфигурации ядер варьировали, но задачу электронного строения по необходимости решали для каждой фиксированной конфигурации.

Именно решению такой задачи и посвящены все описанные выше в главах IV и V методы квантовой химии (теория кристаллического поля, все варианты метода МО ЛКАО, Хц-метод и др.). Ее можно сформулировать вкратце так: для известной ядерной конфигурации молекулярной системы, необходимо определить соответствующее ей электронное строение. Назовем такую постановку прямой задачей квантовой химии.

Легко видеть, что изложенная выше постановка задачи, приводящая к вибронным уравнениям (VI. 13), .как раз обратна