октаэдры, рис. VI.6,б), а для последних трех -она короче двух других (укороченные или сплюснутые октаэдры).

Наоборот, при Л < О и А >0 минимумы поверхности находятся в точках ф = я/З, л, 5л/3, а седлообразные точки - при Ф = О, 2л/3, 4л/3 (при А = 0 мы возвращаемся к прежней картине непрерывной линии минимумов вдоль окружности радиуса ро). При Л > О эти условия меняются на обратные.

Глубины минимумов и высоту барьеров между ними для этих случаев можно найти, подставив в выражение для потенциала е(р, ф) по (VI. 31), координаты соответствующих точек. Для энергии ян-теллеровской стабилизации получаем

(VI. 34)

а для минимальной высоты барьера между минимумами:

Д = 4АЕт./{К: - 2Л)

(VI. 35)

По известному из (VI. 32) значению ро можно найти степень тетрагонального искажения октаэдрического комплекса - разность

длин двух его диагоналей g = 2 7?oi --ог 1 = VS Ро- Решая до конца задачу теории возмущений, можно найти две волновые функции, соответствующие двум решениям (VI. 31) (двум ветвям поверхности адиабатического потенциала)

-= cos-у - sin - я1)2

+ = sin -- -f cos ilj2

Л 8тф- Apsm2(p А cos ф Ар cos 2ф

(VI. 36)

(VI. 37)

Заметим, что во всех публикациях (до работы [285], см. также [283]) принималось Q = ф, что, как видно из (VI. 37), верно только в линейном приближении при А = 0.

Из полученных результатов видна важнейшая роль констант /4 и Л, в связи с чем весьма актуален вопрос об их вычислении.

В приближении теории кристаллического поля константы А и Л определяются сравнительно просто [276, 277]. Действительно, матричный элемент Уц определяется непосредственно по формуле (IV. 7), так что, используя соотношения

ЕдУ дRl

дУ дУ dRi UMlJQi

dRi dRi dRi dQs d Rt

(последнее есть следствие унитарности преобразования декартовых координат к нормальным), можно получить (штрихи в правой

части означают производные)

dVi \ 2 V3

А==и) =--ф (/о) 2 I. dQl J 7

Ф (Ro) = eg

F2{Ro) + YFi [Ro)

(VI. 38) (VI. 39)

(VI. 40)

a Fk{R) даются формулой (IV.8).

Расчеты по этим формулам показали, однако, что они едва ли пригодны для количественного определения вибронных констант. Этого следовало ожидать, ибо грубость приближения кристаллического поля не позволяет вычислить достаточно точно характеристики системы, критически зависящие от характера связи металл - лиганд [в выражения (VI. 38) - (VI. 40) входят первые и вторые производные от матричного элемента вибронного взаимодействия по межатомному расстоянию].

Силовая константа К может быть оценена по известной частоте е-колебания ( продольное колебание в минимуме характеризуется константой К - 2Л).

Более точные результаты получаются при расчетах адиабатического потенциала методом МО ЛКАО, в котором определяют полную энергию системы в различных точках нормальных координат ядер, соответствующих различным пространственным конфигурациям системы (см., например, упомянутые в разделе V. 5

расчеты дляСиРе [180], в которых получено g~ 0,3-0,4А; CuClf [163, 183], VCI4, NiCl [183], Си(Н20)Г, Сг(Н20)б и Мп(Н20)б* [179], СиС1б~ [286] и др.; см. также [182]). В таком расчете автоматически определяется и К. Однако и в этом случае техника расчетов не достигла уровня, когда константы вибронной связи могут быть вычислены с достаточной точностью. В прикладных задачах эти константы остаются параметрами теории.

Случай Г-терма. Тетрагональные, тригональные и орторомбические минимумы

Другой важный случай электронного вырождения - трехкратные Г,- и Гг-термы, актуальные в кубических системах. Ввиду полного подобия результатов рассмотрим здесь только случай Га-терма. Его три электронные функции я]?!, и преобразуются как произведения координат ху, xz и yz соответственно (см. табл. V. I).

Случай Гг-терма существенно сложнее рассмотренного выше £-терма, прежде всего потому, что здесь наряду с тетрагональными искажениями типа е вырождение снимается также при три-гональных искажениях типа <2, описываемых нормальными координатами Qi, Q5 и Qg из табл. VI. 1 ([Гг X al = i + £ + 72).

Рассмотрим сначала линейный случай. Возмущение вырожденного терма линейными членами из V по (VI. 18) содержит наряду с двумя членами выражения (VI. 21) еще три члена типа {dVldQi)oQi (t = 4, 5, 6). Выражая все матричные элементы через минимальное число констант, требуемое теоремой Вигнера - Эккарта (111.35), можно существенно упростить секулярное уравнение теории возмущений. Оно принимает вид [274]:

-ЛОз-е Здесь

2-AQ3-1-

AQ2 - е

лдз-е

\ ЭОз Л

(SVii\ \ dQ, Jo

(VI. 41)

(VI. 42) (VI. 43)

константы связи электронов с тетрагональными и тригональными колебаниями.

Уравнение третьего порядка относительно е (VI. 41) определяет, вообще говоря, три корня el (i = 1, 2, 3), являющихся поверхностями в пятимерном пространстве тетрагональных Q2 и Сз и тригональных Q4, Qs и Qe смещений. Определение аналитического вида этих поверхностей в общем виде едва ли возможно.

Рассмотрим сначала наиболее простой частный случай, когда В =0, А ФО (сокращенно Т - е-задача). В этом случае уравнение (V. 41) решается непосредственно: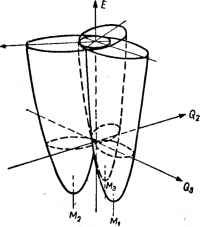

AQ,

e2 = AQ, + AQ,

Рис. VI. 7. Форма адиабатического потенциала для 7-терма в пространстве нормальных координат Qj и Q3.

3 = -kAQ,-

(VI. 44)

Подставляя эти значения в выражения (VI. 20), мы получим для поверхности адиабатических потенциалов некоторую совокуп-\ ность параболоидов, из которых содержащие координаты Q2 и Q3 ] имеют смещенные из начала координат положения равновесия. 1 В пространстве этих координат, таким образом, поверхность ; имеет вид трех пересекающихся параболоидов (рис. VI. 7).

214 I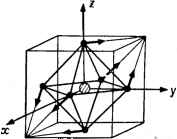

* Положения трех минимумов на плоскости (Qa, Q3) даются координатами

(Ос. 0). Оо. Оо), {~Qo. Оо) (VI. 45)

где Q,) = A/Ka, Ка = Ма<Оа, (Юа -частотэ тстрагональных колеба-. НИИ). Для глубины минимумов - энергий ян-теллеровской стабилизации - имеем:

4t = V2/C (VI. 46)

Заметим, что характер поведения листов поверхности в точке вырождения Q2 = Q3 = О (рис. VI. 7) отличается от случая £-терма (рис. VI. 5 и VI. 6): в то время как для Г-терма в этой точке происходит действительное пересечение поверхностей, в случае £-терма она носит характер точки разветвления поверхностей. Соответствующие адиабатическим потенциалам (отдельным параболоидам на рис. VI. 7) волновые функции, в отличие от варианта £-терма, не перемешиваются ядерными смещениями е-типа и остаются ф1 ~ ху; i]52 ~ и 1]5з ~ yz для 1-го, 2-го и 3-го минимумов соответственно.

В другом частном случае Л = О, ВфО (Т - 2-задача) алгебраическое уравнение 3-й степени (VI.41) непосредственно не упрощаются. Опик и Прайс [274] предложили метод, с помощью которого можно определить экстремальные свойства поверхности - корней уравнения (VI. 41) без его полного решения. Для рассматриваемого случая в трехмерном пространстве координат (Q4, Qs, Qe) поверхность e{Qi, q5, Qe) имеет четыре минимума, лежащих на осях Сз кубической системы в точках (miQo, m2Qo, tnQo). Наборы (m, т2, /Пз) принимают значения

(1.1.1); (-1.1, -1); (1. -1. -1) и (-1. -1,1), а

00 = -- (VI. 47)

где Kb = Мь(оь (юь - частота тригональных колебаний типа /g)-

В этих минимумах комплекс искажен вдоль тригональной оси. При этом смещения лигандов из положений правильного октаэдра [на рис. VI. 8 они показаны для минимума (Qo, -Qo,-Qo)] происходят по поверхности описанного куба по направлению к двум его вершинам (по три лиганда к каждой), через которые проходит соответствующая ось третьего порядка [276]. Энергетическая глубина минимума равна:

Рис. VI. 8. Искажение октаэдров в тригональном минимуме 7-терма.

(VI. 48)

Электронные волновые функции в минимумах в этом случае даются выражением:

- (mill), +т2ф2 -Ь/ИзФз)

(VI. 49)

В общем случае линейной Т - (е +/2)-задачи, когда одновременно учитывается взаимодействие как с тетрагональными (АфО), так и с тригональными (ВФО) колебаниями, поверхность адиабатического потенциала в пятимерном пространстве пяти нормальных координат ( = 2, 3, 4, 5, 6), в целом довольно сложна, но методом Опика и Прайса [274] можно сравнительно несложно определить ее экстремальные точки. Оказывается, что в этом случае альтернативно реализуются либо тетрагональные, либо тригональные минимумы в зависимости от соот-нощения между константами. При {АУ2Ка) > {В/ЗКь) в точках (VI. 45) реализуются тетрагональные минимумы. При этом указанные выше тригональные точки тоже являются экстремальными, но не минимумами, а седлообразными точками. Наоборот, при (Л2/2/Са) < {2ВУЗКь) минимумы образуются в четырех триго-нальных точках, а тетрагональные точки являются седлообразными. В обоих случаях имеется еще один тип экстремальных точек поверхности - шесть эквивалентных по симметрии экстремумов орторомбического типа, с промежуточной энергией

ят = 1-ят + 4ят

(VI. 50)

которые в линейном приближении всегда являются седлообразными точками.

В частности, когда {А/2Ка) = (2В/ЗКь) все три типа экстремальных точек находятся на одинаковой глубине:Еят = £ят = £ят. и на поверхности реализуется непрерывный лист минимумов одинаковой глубины (двумерный желоб в пятимерном пространстве), охватывающий все экстремальные точки [287] (ср. со случаем линейной Е-е-задачи, приводящей к линейному желобу в двумерном пространстве).

Для констант линейной вибронной связи А и В в приближении теории кристаллического поля можно получить следующие выражения [276, 277]:

[92 (о)-54(0)] (VI. 51)

(VI. 52)

Их можно использовать для качественной ориентировки (но едва ли они позволяют получить сколь-нибудь точные количественные оценки этих величин). В частности, так как для рассматриваемых значений Ro F2 (Ro) I > I К (R) I и F2 (Rn) < О (см. Приложение I и таблицы [288]), то Л < () и октаэдры в равновесных конфигурациях минимумов адиабатического потенциала Гг-терма в этом приближении ожидаются сплюснутыми.

В квадратичном приближении вибронная задача Т - (6 + 2) очень сложна и была решена лишь недавно [280, 281, 289]. Как и в случае £-терма оказалось, что квадратичные члены V по (VI. 18) существенно меняют форму поверхности адиабатического потенциала Г-терма. С учетом этих членов секулярное уравнение (VI. 41) усложняется, причем в соответствии с теоремой Вигнера-Эккарта (111.35) необ.ходимо ввести [дополнительно к Л и В по (VI. 42) и (VI. 43)] еще три вибронные константы связи с квадратичными е-, 4- и перекрестными е X 2-колебаниями. Из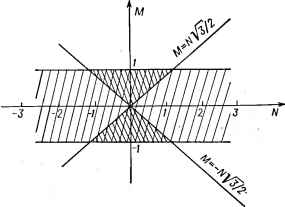

Рис. VI. 9. Область существования тетрагональных (одинарная штриховка) и тригональных (двойная штриховка) минимумов адиабатического потенциала Г - (е-f 2)-задачи на плоскости параметров М и N.

них наиболее существенны в изменении формы поверхности смешанные колебания типа е х 2- Поэтому, имея в виду качественные и полукрличественные результаты, введем одну константу квадратичной связис е X 2-колебаниями

dVis

(VI. 53)

и рассмотрим зависимость поверхности адиабатического потенциала от пяти констант Л, В, С, Ка и Къ. Оказывается, что две безразмерные комбинации этих констант достаточны для описания основных характеристик поверхности:

м=С1КаКьГ: N===BCIAKa (VI. 54)

На плоскости (М,Щ (рис. VI. 9) случаю линейной вибронной связи С = 0 соответствует точка начала координат (0,0). На линиях М=±:Ы/3/2 энергии тетрагональных и тригональных экстремумов (глубины и положения которых не меняются с учетом квадратичного е X -взаимодействия) совпадают. В области