(подробнее см. ниже, раздел VI. 3). Ситуация в целом получается аналогичной эффекту Яна -Теллера для случая электронного вырождения, если считать, что в точке сближения потенциалов происходит их псевдопересечение (показанное на рис. VI. 3,6 пунктиром). Отсюда название явления - псевдоэффект Яна-Теллера.

Как видно из самой формулировки, теорема Яна - Теллера не относится к линейным многоатомным молекулам. Однако при наличии электронного вырождения линейным молекулам присущи особенности, аналогичные описанным выше для нелинейных молекул. Это было показано Реннером [270] на примере трехатомной молекулы задолго до опубликования работы Яна и Теллера [266] *.

Для линейных молекул с электронно-вырожденным в точке термом, все матричные элементы типа (VI. 16) для линейных членов разложения (VI. 15) равны нулю, и поэтому в линейном приближении расщепления вырожденного терма не происходит (точка

e(Q)

Рис. VI. 4. Поведение адиабатических потенциалов в точке вырождения в случае, эффекта Реннера: с-слабый эффект-отсутствие неустойчивости; б - сильный эффект-динамическая неустойчивость.

Q° экстремальна). Однако с учетом квадратичных членов (VI. 15) всегда найдутся такие ядерные смещения, которые расщепляют адиабатический потенциал (эффект Реннера). При этом возможны два случая эффекта Реннера:

слабый, когда константа эффекта [матричный элемент квадратичного члена электронно-колебательного взаимодействия (,dV/6Ql)o] мала настолько, что расщепление не приводит к неустойчивости основного состояния (рис. VI.4,а).

сильный, когда из-за большого расщепления состояние нижнего листа адиабатического потенциала становится неустойчивым . (рис. VI. 4, б) [в этом случае загибание кривой вверх обеспечи- вается за счет четвертых степеней разложения (VI. 15)].

Таким образом, и в случае линейных молекул при наличии электронного вырождения и достаточно сильной электронно-колебательной связи адиабатический потенциал не имеет минимума. Однако в отличие от нелинейных молекул здесь (de/dQ) п = о для

всех Qv, точка вырождения экстремальна, но (d\/dQl) о < О, т. е.

эта точка соответствует максимуму поверхности (в этом сечении).

* Именно работа Р Реннера, ученика Э. Теллера, явилась предметом упомянутой выше дискуссии с Л. Д. Ландау, которая привела к формулировке теоремы Яна - Теллера.

В условных терминах неустойчивости такая система может быть названа динамически неустойчивой, в отличие от случая нелинейных молекул, которому соответствует статическая неустойчивость.

Заметим также, что в разложении электронно-колебательного взаимодействия (VI. 15) константы при членах второго порядка обычно заметно меньше констант при членах первого порядка. На этом основании можно полагать, что эффект Реннера, появляющийся в результате учета членов (VI.15) начиная со второго (квадратичный эффект), окажется соответственно слабее эффекта Яна -Теллера (линейного эффекта). По теории эффекта Реннера см. также [270, 271].

В приведенном обсуждении формулировки и интерпретации теоремы Яна - Теллера мы ограничились для простоты орбитальным вырождением в электронной подсистеме. Все сказанное относится и к спиновому вырождению [272], за исключением двукратного спинового вырождения для систем со спином S = V2 (так называемое крамерсово вырождение). Следует, однако, отметить, что влияние чисто спинового вырождения на электронное строение и свойства системы значительно слабее орбитального, так что до сих пор подавляющее большинство исследований посвящено последнему.

VI.3. АДИАБАТИЧЕСКИЕ ПОТЕНЦИАЛЫ ПРИ НАЛИЧИИ ЭЛЕКТРОННОГО ВЫРОЖДЕНИЯ И ПСЕВДОВЫРОЖДЕНИЯ

Как указывалось выше, для определения движений ядерной системы при наличии электронного вырождения или квазивырож-цения (псевдовырождения) необходимо решить сложную систему электронноколебательных (вибронных) уравнений (VI. ГЗ), а это требует прежде всего знания адиабатических потенциалов em(Q). Последние представляют и самостоятельный интерес, ибо, как будет показано ниже, они позволяют получить ряд качественных и полуколичественных выводов о свойствах системы без решения уравнений (VI. 13). Схема приближенного расчета формы адиабатических потенциалов для ряда актуальных случаев сравнительно несложна *.

Прежде всего примем во внимание, что обычно встречающиеся случаи электронного орбитального вырождения цо кратности равны либо f = 2 (£-терм), либо f = 3 (Г-терм) (без учета спинового вырождения). Причем последнее присуще только высокосимметричным кубическим комплексам (октаэдр, тетраэдр, куб), и поэтому достаточно исследовать только эти два случая. Более высокие кратности орбитального вырождения - f = 4 и f = 5 - могут реализоваться в редких случаях, например, икосаэдрической координации.

Далее, разделим, как обычно, все электроны на внутренние и валентные и предположим, что в вибронное взаимодействие

См. [267, ch. 3; 273-284].

V{q,Q) вносят вклад только последние, а внутренние электроны вместе с ядрами образуют атомные остовы, взаимодействие между которыми может быть аппроксимировано гармоническим членом

(VI. 17)

где Ка = Маа - силовая константа а-го нормального колебания (Ма - его приведенная масса; to - частота).

Пусть теперь при решении электронной части уравнения Шредингера (VI. 3) с потенциалом V (q, QV) для фиксирований точки Q = Qa мы получили /-кратно вырожденный терм. При малых от- клонениях Qa от Qa потенциал V(q, Q) не очень сильно отличается от V (q, Qa), так что разность

У = У{1 Qa)-n. Q) = Z()o(2a-Qa) +

может считаться малым возмущением.

Решая задачу теории возмущения для вырожденного терма, мы придем к секулярному уравнению

f/-A/l = 0 (г,/ = 1,2.....П (VI.I9)

которое имеет / корней 8fe(Qa). Очевидно, что полный адиабатический потенциал thiQa) есть сумма электронной части (Qa) и взаимодействия остовов W°{Qa):

nea) = ]-2]aQa + efe(Q )

Случай £-терма. Мексиканская шляпа

(VI. 20)

Для вычисления матричных элементов Уц в уравнении (VI. 19) примем во внимание, что они представляют собой интегралы типа (VI. 16) и отличны от нуля, если произведение представлений, по по которым преобразуются волновые функции вырожденного терма i и фз, содержит в себе представление, по которому преоб-

разуется соответствующий член {-щ или (-qJ из (VI. 18) (см. раздел (III.4). В случае Е-терма обе функции преобразуются по £-представлению и так как [Е X E] = Ai-\- Е, то отличны от нуля только те матричные элементы, которые соответствуют смещениям ядер (или колебаниям) щ- и е-типа. Из них йрколебания полносимметричны, не искажают комплекса и не снимают вырождения электронного терма. Поэтому они нас не будут интересовать здесь (их можно исключить из конечного результата

надлежащим выбором начала отсчета. Единственно активными остаются двукратно вырожденные е-колебания, так что сокращенно рассматриваемый случай иногда называют Е-е-задачей.

Форма нормальных колебаний е-типа, Q2 и Q3 и их выражение через декартовы координаты для октаэдра и тетраэдра даны на рис. VI. 1 и VI.2 и в табл. VI. 1. По виду смещений ядер в случае октаэдра (рис. VI. 1) они называются тетрагональными. Примем, что в точке электронного вырождения Qi = Qli - 0. Для этих же случаев две электронные функции С-терма преобразуются как функции ifi = rfz и -фг = соответственно (см. табл. V. 1).

Эти данные позволяют сравнительно просто вычислить матричные элементы членов V, содержащих колебания Q2 и Q3.

Рассмотрим сначала линейное по вибронному взаимодействию приближение, когда в возмущении V по (VI. 18) учитываются только линейные по Q члены. Тогда возмущение, дающее отличные от нуля поправки, принимает вид

(V1.21)

И для заполнения секулярного уравнения (VI.19) второго порядка необходимо вычислить восемь матричных элементов типа (dViildQi). Однако, используя теорему Вигнера -Эккарта (раздел III. 4), мы можем непосредственно выразить все эти матричные элементы через одну константу - приведенный матричный элемент. Выберем последний в виде

(VI. 22)

(А имеет смысл константы линейной вибронной связи, характеризующей скорость изменения электронных состояний с изменением межатомных расстояний). Тогда секулярное уравнение для рассматриваемого случая принимает вид:

- AQi - e AQs AQ2 AQs - b

(VI. 23)

Его корни находятся непосредственно:

1.2 =

miVq1+q1

(VI. 24)

Подставляя эти значения е в формулу (VI. 20), мы получим выражение для адиабатического потенциала в виде:

8 (Qg. q3) = J ( 2 + QD±\A\ Vq + Q (VI. 25)

Последнее было получено впервые Ван Флеком [84]. Форму поверхности e(Q2, Q3) удобнее представить наглядно, если перейти к координатам р и ф:

Qj = psln9, Q3==pcosqJ (VI. 26)

Тогда

С(р. ф) = -/!Гр±Мр

(VI. 27)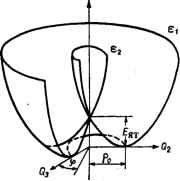

откуда видно, что е не зависит от ф (рис. VI. 5). Из-за своей формы эта поверхность получила название мексиканская шляпа .

Как следует из рис. VI. 5, точка Q2 = Qs = О есть точка пересечения двух ветвей поверхности ei и ег, а минимумы ее расположены вдоль окружности с радиусом ро = Л С на глубине £ят = = Л72/С. Отсчитанная от точки пересечения термов (точки вырождения) EfiT называется энергией стабилизации в эффекте Яна-Теллера. Для октаэдрической системы, например, минимумы поверхности с учетом формы смещений Q2 и Qs (см. рис. VI. 1) соответствуют таким искажениям октаэдра, при которых шесть лигандов остаются попарно на трех взаимно перпендикулярных тетрагональных осях, причем лиганды каждой пары расположены на одинаковом расстоянии от центра но обе его стороны, а суммы квадратов этих расстояний для трех пар во всех точках минимумов остаются постоянными. В этом случае можно предположить, что с учетом динамики ядра будут свободно перемещаться вдоль окружности радиуса Ql-f Q3 = po. непрерывно меняя пространственную конфигурацию системы в пределах описанных выше искажений. Вдоль остальных координат (Э (а Ф 2,3) поверхность адиабатического потенциала (VI. 20) имеет параболическую зависимость с минимумом в точке Qa = Qa. С учетом квадратичных членов вибронного взаимодействия в возмущении (VI. 18) можно все матричные элементы выразить через один - на основе теоремы Вигнера - Эккар-та (аналогично линейному случаю). Тогда секулярное уравнение теории возмущения принимает вид [279]

-AQz + A(Ql-(i)-e AQ2-2AQ,Q

AQ2 - 2AQ3 AQ, - л (Ql - Ql) - e где A - константа квадратичного взаимодействия;

Корни уравнения (VI. 28) определяются непосредственно !

Рис. VI. 5. Форма адиабатического потенциала в случае £-терма (без учета квадратичных членов электронно-колебательного взаимодействия) ( мексиканская шляпа ).

= О (VI. 28)

± р л/а + Лр -f 2ЛЛр cos Зф

(VI. 30)

где координаты р и ф выражаются через Q2 и Q3 по (VI. 26). Отсюда для адиабатического нотенциала в отличие от (VI. 27) получаем:

е (р, (f) = j кр ± р л/а + ЛV -f 2ЛЛр cos Зф

Его экстремальные точки даются выражениями:

± Л

Ро-УС + (-1) 2Л Ф = пя/3 (п = 0, 1,.... 5)

(VI. 31).

(VI. 32)

При этом верхний знак соответствует случаю Л > О, а нижний - Л < О, причем предполагается, что К > 2А.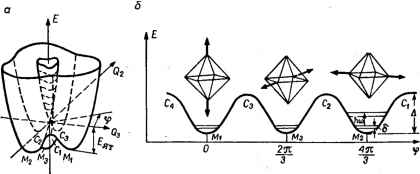

Рис. VI. 6. Три минимума адиабатического потенциала для £-терма:

с-в пространстве нормальных координат Q, и Qj; (Ati, М М,-минимумы; Ci, С, и С -седлообразные точки); б-как функция угла q> с указанием направления Искажения октаэдра в каждом из них.

Для случая Л < О вторые в экстремальных точках г/==5д

производные

с точностью

функции (VI. 31) до членов

(VI. 33)

А/К удовлетворяют соотношению [275]:

азз = *:-(-1) 7Л

Отсюда следует, что при Л < О в трех точках п = О, 2, 4 (т. е. при ф = О, 2л/3 и 4л/3, рис. VI. 6) поверхность имеет минимумы [так как в соответствии с условиями минимума функции двух переменных в этих точках первое выражение (VI. 33) отрицательно, а второе положительно], а в других трех точках при п-\, 3, 5 (ф = л/3,л,5л/3) поверхность имеет седлообразные точки.

Переход к обычным декартовым координатам по формулам табл. VI. I показывает, что всем этим точкам соответствуют тетрагонально искаженные октаэдры, причем для первых трех точек одна диагональ длиннее двух других (удлиненные или вытянутые