поле (см. раздел IV. 2). Зная, как должны расщепляться те или иные колебания (и их частоты) в полях различной симметрии (что определяется непосредственно методами теории групп, табл. IV. 3, стр. 80), можно использовать колебательную спектроскопию и для исследования влияния окружения на координационную систему (или ее колеблющийся фрагмент). Наличие высокой симметрии и возможность ее использования для упрощения исследования - одно из особенностей колебательной задачи для координационных систем.

Другая существенная особенность связана с отмеченной ранее (стр. 12) трехмерной делокализацией электронного облака координационной химической связи, приводящей к отсутствию характеристичности колебаний металл - лиганд. При наличии разных лигандов в общем случае невозможно выделить отдельное колебание металл- лиганд и считать его хотя бы приблизительно одинаковым при переходе от одного комплекса к другому. Трехмерная делокализация электронного облака приводит к коллективизации связей, и колебания, как правило, должны рассматриваться для всей С41стемы в целом. В этом заключается одно из основных отличий колебательной спектроскопии координационных соединений от спектроскопии органических валентных соединений.

И, наконец, частоты колебаний координационных систем характеризуются большим разнообразием и охватывают широкий диапазон, простирающийся далеко в низкочастотную область - до десятков см-. Дополнительные экспериментальные трудности исследования в этой области частот, требующие специальных спектрографов, в широких масштабах преодолеваются лишь в последние годы. Анализу инфракрасных спектров и колебаний координационных систем посвящены монографии [261-265].

VI.2. ТЕОРЕМА ЯНА-ТЕЛЛЕРА

Электронно-колебательные уравнения при наличии электронного вырождения

При наличии электронного вырождения или близких электронных уровней отбрасывание членов AmhXkiQ) в системе уравнений (VI. 5) незаконно. Действительно, если полученный при решении уравнения (VI. 3) электронный терм вырожден, или почти вырожден, то поправка к функциям фй(9,Q), учитывающая зависимость от ядерных смещений Q, будет иной, чем в (VI. 8) (см. [29, с. 168])

Ф, 7. о)-Ф,(?. +Z\,k-w Е

/=1 m=f+i *

е Ф/(?. 0)-f fc*. - ь

/=f+l * I

где / - кратность вырождения. 200

(VI. 12)

Здесь первая сумма дает поправку на перемешивание рассматриваемой функции с другими из того же набора /-функций, образующих вырожденный терм, а вторая - взаимодействия со всеми остальными возбужденными состояниями. Последние имеют тот же порядок величин, что и поправки к функции невырожденного терма (VI. 8), и поэтому могут быть игнорированы как и в обычном адиабатическом приближении. Однако первая сумма содержит знаменатели с разностями Wuh-VFjj, которые при малых Q могут стать сколь угодно малыми (при этом может нарушиться критерий применимости теории возмущений). Эти члены не могут быть игнорированы и связанные с ними члены Amh в системе уравнений (VI. 5) не могут быть отброшены. В этом случае критерий адиабатического приближения в форме (VI. 10), вообще говоря, не выполняется.

Отсюда следует, что при наличии электронного вырождения адиабатическое приближение неприменимо. Это существенно усложняет исследование задачи.

В том же приближении, в котором были получены колебательные уравнения адиабатического приближения (VI. 9), можно сохранить в (VI. 12) только первую сумму поправочных членов, и бесконечная система уравнений (VI.5) переходит в конечную систему / уравнений:

(VI. 13)

При этом полная волновая функция также содержит / членов:

1(9, Q) =

i%t{Q)<fi(q> Q)

(VI. 14)

Основной вывод, следующий из (VI. 13) и (V. 14), состоит в том, что при наличии электронного вырождения отдельные электронные состояния вырожденного терма теряют физический смысл, так как они полностью перемешиваются ядерными смещениями. С другой стороны, и ядерные колебания в этом случае - в отличие от случая невырожденного терма - нельзя более рассматривать как зависящие только от одного электронного состояния; ядерные и электронные движения полностью перемешиваются и состояния системы становятся электронно-ядерными (виброн-ными).

Формулировка теоремы Яна-Теллера и ее содержание

Задача движения ядер при наличии электронного вырождения существенно отличается от задачи для невырожденного случая не только тем, что в первом случае необходимо решить систему уравнений (VI. 13) вместо одного уравнения (VI. 9); не менее важно

то обстоятельство, что для электронного вырождения форма адиабатического потенциала em{Q) гораздо сложнее. Именно к поведению адиабатического потенциала вблизи точки вырождения относится теорема Яна - Теллера.

Предположим, что при решении электронного уравнения (VI. 3) адиабатического приближения для некоторой симметричной конфигурации ядер, описываемой точкой Qa (а = 1, 2, Л) (Q - нормальные координаты для этой симметричной конфигурации), мы получили два совпадающих значения адиабатического потенциала ei (Qa) = Вг (Qa), которым соответствуют две электронные функции 41 и 42- Как ведут себя эти потенциалы вблизи точки

Для исследования этого вопроса разложим энергию взаимодействия электронов и ядер V(q, Q) в ряд по небольшим смещениям вблизи точки QI [ср. с (VI. 7)]:

-iZ() ( .- Dt...

Решение электронного уравнения при фиксированных в точке Qa ядрах равносильно учету в нем лишь первого члена V (q, Qa) разложения (VI. 15), Считая смешения Qa -Qa достаточно малыми, мы можем учесть влияние следующих членов в виде малого возмущения.

Если адиабатический потенциал имеет в точке Qa минимум, то {de/dQa)o = 0 и e(Q ) не содержит линейных членов ядерных смещений Qa - Qa. Это, в свою очередь, возможно, если все матричные элементы линейных членов разложения (VI. 15), построенные на функциях 41 и Чг, равны нулю. Другими словами, если хотя бы один из матричных элементов

(VI. 15)

(VI. 16)

отличен от нуля, то адиабатический потенциал в точке Qa не имеет минимума.

Ян и Теллер впервые показали* [266], что для любой многоатомной системы при наличии электронного вырождения в нелинейной симметричной конфигурации ядер всегда найдутся такие

* По признанию Теллера, приведенному в виде Исторического замечания к вышедшей недавно книге, посвященной эффекту Яна - Теллера [267], идея эффекта принадлежит Л. Д. Ландау, который отстаивал ее в дискуссии с Телле-ром во время их совместного пребывания в Копенгагене в 1934 г, В последующие два года Ян и Теллер перебором всех точечных групп симметрии убедились, что идея Л. Д. Ландау в применении к нелинейным молекулам верна. По этой причине Теллер считает, что эффект должен носить имя Л. Д. Ландау. Более полные доказательства теоремы см. в работах [268],

ядерные смещения Q, для которых интеграл (VI. 16) отличен от нуля.

Доказательство этого утверждения проводится непосредственно при помощи теории симметрии. Действительно, можно показать (раздел III. 4), что интеграл типа (VI. 16) отличен от нуля в том случае, когда произведение представлений, по которым преобразуются подынтегральные выражения, содержит единичное пред-, ставление. Представления, по которым преобразуются волновые функции вырожденного терма данной симметричной конфигурации ядер, хорошо известны. Что касается представления, по которому преобразуется производная (dV/dQ), то оно совпадает с таковым для Qa [ибо произведение (dF/dQJo(Qa - Qa), как и все

е(0)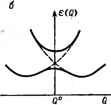

Рис. VI. 3. Поведение адиабатических потенциалов вблизи точки вырождения в эффекте Яна - Теллера (а) и вблизи точки псевдопересечения (показано пунктиром) в псевдоэффекте Яна - Теллера (б).

члены гамильтониана, должно преобразоваться по поЛносиммет-ричному представлению], т. е. с представлением, по которому преобразуется соответствующее нормальное колебание.

Перебрав все возможные точечные группы, можно показать, что в любой из них для каждого типа симметрии вырожденного электронного терма всегда найдутся в той же группе такие типы симметрии нормального колебания, сочетание которых приводит к отличию от нуля интеграла (IV. 16).

На рис. (VI. 3, о) показан схематический ход адиабатического потенциала в рассматриваемом случае двукратного электронного вырождения как функция координаты Qv, для которой интеграл (VI. 16) отличен от нуля. В точке вырождения Qv = Qv адиабатические потенциалы пересекаются, а вне этой точки происходит расщепление и снятие вырождения. Любое расщепление (при сохранении центра тяжести терма) приводит к понижению энергии основного подуровня расщепления, поэтому неполносимметричные конфигурации с Qv Ф Qv энергетически более выгодны [до тех пор, пока не преобладают квадратичные члены потенциальной энергии ядер типа V2K(Qv -QvT см. раздел VI. 3] и это может служить дополнительной иллюстрацией к теореме.

На основе сказанного можно привести следующую общую формулировку теоремы Яна - Теллера [269]:

если адиабатический потенциал нелинейной многоатомной системы e(Qi, Q2,...,Qn), являющийся формальным решением электронной части уравнения Шредингера, имеет несколько пересекающихся ветвей, то в точках пересечения Qo = Qa, а= 1, 2, .... ц

всегда найдутся такие ядерные смещения Qv, для которых ((3e/(5Qv)qo =70; следствием этого является то, что e(Qi,Q2.....Qu)

в точке Qa не имеет минимума.

Расчеты показывают (см. ниже), что для двукратно вырожденного электронного £-терма активными в смысле теоремы Яна - Теллера, т. е. снимающими его вырождение, являются двукратно вырожденные нормальные колебания е-типа (табл. VI. 1), а для трехкратно вырожденного Г-терма ими могут быть как е-колеба-ния, так и трехкратно вырожденные /г-колебания (раздел VI.3).

Интерпретация теоремы в терминах неустойчивости и ее критика [269]

Отсутствие минимума адиабатического потенциала в точке электронного вырождения обычно интерпретируется как неустойчивость ядерной конфигурации в этой точке. Поэтому чаще всего встречается формулировка теоремы Яна - Теллера в виде утверждения: нелинейная многоатомная система в ядерной конфигура-ции с вырожденным электронным термом неустойчива. При этом утверждение о неустойчивости системы истолковывается в том смысле, что она самопроизвольно искажается так, чтобы электронный терм расщеплялся и основное состояние оказалось невырожденным.

Такая формулировка и интерпретация теоремы Яна -Теллера, исходящая от самих ее авторов [266], и перенесенная затем в ряд монографий и учебных пособий (см., например, [29, § 102]), получила широкое распространение среди исследователей, использующих эту теорему для толкования экспериментальных данных. Между тем, реальная ситуация в системах с электронным вырождением, как будет показано ниже, значительно сложнее простого утверждения о неустойчивости. Более того, понятое буквально такое утверждение просто неверно и может привести к грубым ошибкам.

Как было показано выше, вывод об отсутствии минимума E(Qa) В точке электронного вырождения следует из решения электронной части уравнения Шредингера и, поэтому, не может относиться к поведению ядерной подсистемы в рассматриваемой ситуации. Последнее, естественно, определяется решением уравнений для ядерной подсистемы и может быть получено только после их решения. Отсутствие минимума у функции e(Qa) можно непосредственно интерпретировать как неустойчивость, вообще говоря, лишь только в отсутствие электронного вырождения. Действительно, в этом случае электронное и ядерное движения разделяются, так что адиабатический потенциал e(Qa), как указывалось, имеет смысл потенциальной энергии ядер в среднем поле всех электронов, и, следовательно, производная (<3e/c)Qv)o означает обобщенную силу, которая действует на ядра в точке Qa. Поэтому здесь условие (de/dQv)o#0 можно интерпретировать

как отличие от нуля действующей на ядра некомпенсированной искажающей (в сторону ядерных смещений Qv) силы, делающей ядерную конфигурацию Qa неустойчивой.

Однако при наличии электронного вырождения адиабатический потенциал e(Qa) уже не имеет смысла потенциальной энергии ядер в поле электронов, ибо движение электронов и ядер более не разделяется. В этом случае e(Q ) теряет наглядный физический смысл, становясь формальным понятием. Поэтому в данном случае приведенные выше рассуждения о неустойчивости и искажающих силах, строго говоря, неприемлемы. Используемое здесь как термин слово неустойчивость следует понимать формально - как отсутствие минимума адиабатического потенциала, а не как характеристику поведения ядерной подсистемы. Последнее, как указывалось, выясняется только после решения уравнений динамики движения ядер. Как будет показано ниже, в общем случае квантовомеханически понимаемая конфигурация ядер при наличии электронного вырождения не искажается. При этом и вырождение терма не снимается, а переходит из электронного в вибронное.

Необычное поведение адиабатического потенциала системы вблизи точки электронного вырождения и вытекающие из этой ситуации физические следствия в литературе объединяются под названием эффекта Яна -Теллера.

Псевдоэффект Яна-Теллера. Эффект Реннера

Из приведенного выше обсуждения адиабатического приближения и его неприменимости к случаю электронио-вырожденного терма однозначно вытекает, что вполне аналогичные явления должны быть и тогда, когда электронные термы не вырождены, но энергетически достаточно близки между собой. Действительно, для близких уровней критерий адиабатического приближения (VI. 10) не выполняется, поправки к электронной функции, учитывающие зависимость от ядерных координат (VI. 12), и с ними члены Amh в уравнениях (VI. 5), достаточно велики и не могут быть отброшены. Следовательно, колебательная задача для близких электронных состояний, как и в случае вырождения, сводится к решению системы уравнений (VI. 13), а не отдельных уравнений (VI. 9) для каждого электронного состояния. Поэтому ситуацию с достаточно близкими электронными уровнями иногда называют квазивырождением.

Проведенная аналогия между вырождением и квазивырождением распространяется и на поведение адиабатического потенциала вблизи области квазивырождения. На рис. VI. 3,6 показан случай, когда в пространстве ядерных смешений Q вблизи точки Q = Qo электронные уровни достаточно близки между собой, причем матричный элемент А по (VI. 16) предполагается отличным от нуля. В этом случае два уровня взаимодействуют - отталкиваются, в результате чего основное состояние становится неустойчивым в смысле отсутствия минимума потенциала в точке Q°