и обозначим линейный по Q член посредством W = (~)о

Тогда при решении электронного уравнения с учетом только нулевого члена разложения (VI. 7) мы получим систему функций фй(9. 0), не зависящую от Q. Учитывая теперь влияние члена W в виде малого возмущения, мы найдем поправки к функции

(VI. 8)

откуда видно, что производные от фй по Q в (VI. 6), а вслед за ними и все выражение (VI. 6), отличны от нуля только за счет малых поправочных членов в (VI. 8), содержащих большие знаменатели (eh - Bj)-разности энергий основного и возбужденных электронных состояний, и по этой причине малы.

Без учета членов Amh уравнения (VI. 5) разбиваются на простые уравнения, отдельные для каждого %m(Q)

x (Q) = o

(VI. 9)

и, следовательно, каждому фт(9, Q) соответствует свой набор %m(Q). При этом состоянию системы в целом соответствует волновая функция (q,Q) = ({>m(q,Q)%n,(Q).

В уравнении (VI.9) член em(Q) есть средняя энергия электронов при фиксированном положении ядер плюс энергия взаимодействия между ядрами и имеет смысл потенциальной энергии ядер; он называется адиабатическим потенциалом, а уравнение в целом есть не что иное как уравнение Шредингера для движения ядер в рассматриваемом приближении.

Таким образом, решение полного уравнения Шредингера (VI. 1) после отбрасывания некоторых членов, которые в отсутствие электронного вырождения предполагаются малыми (см. ниже) свелось к двум более простым этапам; сначала решается электронное уравнение (VI. 3) при фиксированных ядрах и затем полученный при этом адиабатический потенциал em(Q) используется для решения задачи о движении ядер. Это и есть широко известное адиабатическое приближение (VI. 9).

Из сказанного вытекает следующий количественный критерий применимости адиабатического приближения: необходимо, чтобы-расстояние между уровнями колебательной задачи (VI. 9), т. е. величина кванта колебаний йсо, было значительно меньше разности электронных уровней eft -ej [знаменателей в формуле (VI. 8)]:

Ьа<.е - (VI. 10)

Можно привести некоторые оценки порядков величин, из которых явствует степень приближенности результатов метода адиабатического приближения [70]. При получении уравнений (VI. 9) мы должны отбросить члены Удф, Vqjj и /Доф по сравнению с фД(}Х. Заметим, что ф занимает область порядка одной атомной

единицы, в то время как х отлично от нуля лишь в пределах величины порядка с - амплитуды колебаний ядер. Поэтому производная от X будет в 1/а раз больше производной от ф, так что по порядку величин справедливы соотношения: (VQф VQx/фДoзc) ~ а и (хДдф/фАох) ~ а. С другой стороны, обозначая здесь массу электрона и ядра через т и М, силовую константу через К, электронную энергию через и колебательную Е имеем: = = = И (К/М)/ = h (Kim) Ч (т/М) Ч ~ (т/М). Кроме этого ~ Ка и учитывая, что по порядку величин Е ~ 1 ат. ед., К = = 1 ат. ед., получаем, что ~ (т/М)Ч или а ~ (т/М)1\ Отсюда следует, что отброшенные в адиабатическом приближении члены имеют порядок величины корня четвертой степени от отношения масс электрона и ядер. Такой параметр малости адиабатического приближения получается и в более строгой общей теории [253, гл. IV]. Заметим, что, полагая £~ти и мы по-

лучим, что (v/Ve) ~ (mlM)\ т. е. отношение скоростей электронов и ядер по порядку величины равно кубу параметра малости.

Нормальные координаты. Гармонические колебания

Существенное упрощение колебательного уравнения системы (VI. 9) в адиабатическом приближении, допускающее его непосредственное решение, достигается в так называемом гармоническом приближении при введении нормальных координат. В общем случае уравнение (VI. 9) - уравнение ЗЛ переменных координат ядер НЛаауа), а = \,2, N, которое после исключения переменных, характеризующих вращение и перемещение, системы как целого, превращается в уравнение ЗЛ -6 переменных. Для сложной зависимости адиабатического потенциала от координат

Ra переменные в уравнении (VI. 9), вообще говоря, не разделяются. Однако в отсутствие электронного вырождения этот потенциал обычно имеет один абсолютный минимум, соответствующий устойчивой пространственной конфигурации ядер Ra = Ra. Вблизи этого минимума е( ) хорошо аппроксимируется квадратичной зависимостью от R - параболой (гармоническое приближение). В этом приближении зависимость e(Ra) можно привести к так называемому каноническому виду. Иными словами, вместо декартовых координат Х, Y и можно выбрать новую систему координат Qa так, чтобы в этих новых координатах адиабатический потенциал e(Qa) имел вид суммы квадратов QI, е= X <uQ2

(без перекрестных членов типа Q Qp), а кинетическая энергия осталась бы аддитивной функцией производных от Q (приведение квадратичной формы см. [254, с. 120]). Такие координаты называют нормальными.

В определении нормальных координат существенную роль играет симметрия системы. Действительно, так как уравнение (VI. 9)

есть уравнение Шредингера с гамильтонианом, обладающим той же симметрией, что и пространственная симметрия системы, то его собственные функции и значения (а вслед за ними и © ) должны классифицироваться по неприводимым представлениям

группы симметрии задачи (см. раздел III.4). Иначе говоря, неприводимые представления группы симметрии соединения определяют типы симметрии возможных нормальных колебаний, а вместе -с ними -форму колеба-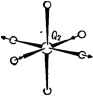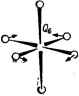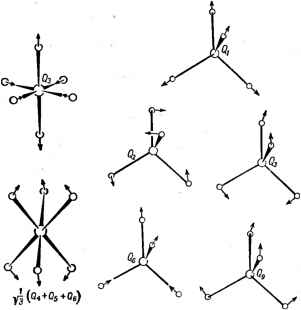

Рис VI. 1. Форма ядерных смещений для наиболее актуальных нормальных колебаний октаэдрического комплекса.

В случае вырожденных колебаний может реализоваться любая их линейная комбинация [например, типа {Qt + Q( + Qt> для колебаний i 1.

Рис. VI. 2. Формы ядерных смещений для наиболее актуальных нормальных колебаний тетраэдрического комплекса.

2gi-

НИИ, кратность вырождения частот и др. Оказывается, что используя методы теории симметрии, можно сравнительно просто заранее определить эти характеристики [29, с. 434; 255, гл. VI; 256; гл. V].

На рис. VI. 1 и VI. 2 показан вид наиболее важных нормальных колебаний октаэдрического и тетраэдрического координационных комплексов, а в табл. VI. 1 - возможные гипы колебаний и выражение нормальных координат Qa через декартовы координаты Ха, Ya и Za.

Нормальные координаты кубических систем, выраженные через декартовы координаты смещения л, Y, Z

Нормальные координаты

Тип симметрии

Выражение через декартовы смещения

Октаэдрическая система МАе симметрии о/,

Тетраэдрическая система MA4 симметрии

(Zi+z2+Z3 + Zt)/2

(yi-y2-Y3 + y,)/2 (Х,-Ха-Хз-ЬХ4)/2

(Z,-Z2-bZ3-Z4)/2 (Z,-bZ2-Z3-Z4)/2 (Z,-Z2-Z3-bZ4)/2

(-X, -I- X2 - Хз -f X4)/4 + л/Н-yi +y2-Y3 + + y,)/4

(- X, - Xj -b Хз -b x4)/4 + V3 (yi +y2-Y3-

-yt)l4 (Х,-ЬХ2-ЬХз-ЬХ4)/2

Координаты одинакового типа симметрии и t\. и не являются нормальными

из-за их взаимодействия между собой. т п л/ ,!1л т,пг

Для группы смещения даиы в единой системе координат, а для i-в локальных

свстеиах на лигандах (см. рис. V. 1, стр. 114).

Число нормальных колебаний Q и соответствующих им частот равно числу колебательных степеней свободы системы ЗЛ -6. Для колебаний вырожденных типов симметрии частоты совпадают. В этом случае отдельные колебания вырожденной совокупности остаются неопределенными - любая их линейная комбинация есть нормальное колебание. В частности, приведенные в табл. VI. 1 и на рис. VI. 1 и VI. 2 формы двукратно вырожденных колебаний .типа е (Qz и Qs) и трехкратно вырожденных типа (Qe) произвольны (с точностью до их любой комбинации внутри вырожденной пары е или тройки ).-При наличии двух или нескольких нормальных колебаний одинакового типа симметрии (например, /г и t в случае тетраэдра, табл. VI. 1) они взаимодействуют между собой (подобно тому, как взаимодействуют между собой электронные термы одинаковой симметрии) и их частоты уже не независимы. Для октаэдрической системы е-колебания называются иногда тетрагональными, а tg - тригональными - по виду искажения, к которому приводят соответствующие ядерные смещения (рис. VI. 1).

Оказывается, что не все типы симметрии колебаний разрещены для данной системы. В табл. VI. 2 показаны возможные типы симметрии колебаний для некоторых систем [29, с. 434; -256, гл. Vl.

Таблица VI. 2

Классификация нормальных колебаний до симметрии для некоторых типов молекул

Число атомов N (число нормальных колебаний

3W-6)

Симметрия

Типы нормальных колебаний

4(6) 5(9) 7(15) 7(15)

9(21)

Та Он

NH3, пирамида МпО, тетраэдр CrFg , октаэдр

MAjBj, тетрагонально искаженный октаэдр

OsFe, куб

А[, Е, Т2, Т2

jg g 2б> 72 , Ji,

A,g, Aig, Л2 , А2ц, Bjg, Bg,

Axg, Лц, Eg, £ , Tju, 7, , T , T2

В нормальных координатах уравнение (VI. 9) разбивается на 3N - 6 уравнений (по числу координат Q), причем каждое из них есть уравнение гармонического осциллятора

-MTO + i Саа = а (а = 1, 2, ..., 37V - 6) (VI. Юа)

где М - так называемая приведенная масса а-го нормального колебания; сОд - его частота.

Как известно, в этом случае

( = 0, 1. 2,...)

(VI. 11)

Т. е. уровни энергии осциллятора меняются только на целые кратные значения fioj. С другой стороны, - собственная частота механических колебаний системы с потенциальной энергией вида V2MaCuaQL т. е. она появляется в виде решения колебательного уравнения вида:

Отсюда следует, что для нахождения частот малых колебаний многоатомной-системы при отсутствии электронного вырождения можно решать механическую задачу собственных колебаний системы ядер с потенциальной энергией взаимодействия e(Qa), аппроксимируемой параболой.

Методы решения таких задач можно найти в специальных руководствах по теории колебаний [256, гл. 8; 257, гл. П]. Важное значение имеют также интенсивности колебательных переходов [258-260].

В заключение следует подчеркнуть также, что представления о нормальных колебаниях приемлемы только в гармоническом приближении, когда вследствие малости амплитуд колебаний (например, при достаточно низких температурах и в отсутствие вырождения) можно пренебречь кубическими и более высокими членами зависимости потенциальной энергии от координат ядер. В противном случае существенны эффекты ангармонизма [256, с. 71; 257, с. 219].

Особенности колебаний координационных систем

Возможные частоты (и формы) колебаний, таким образом, связаны с симметрией системы, и это обстоятельство лежит в основе идентификации колебательных спектров инфракрасного поглощения и комбинационного рассеяния. Чем выше симметрия соединения, тем легче идентификация и анализ электронного строения на основе спектров. Например, для правильной октаэдрической системы из семи атомов возможны всего 3-7 - 6=15 колебаний, объединяемых в группы: одно aig-, два eg-, три tg-, три tiu; три t\u- и три Ти-колебаний (табл. VI. 1 и VI. 2). Каждой из групп вырожденных колебаний соответствует одна и та же частота, так что всего следует ожидать шесть колебательных частот. Из них в инфракрасном поглощении проявляются только нечетные колебания, т. е. три частоты t2u, t\u и tU, а четные колебания aig, eg и hg проявляются только в комбинационном рассеянии [257, с. 277].

Для дальнейшего анализа происхождения колебательных частот можно использовать представления о расщеплении вырожденных колебаний в полях более низкой симметрии, вполне аналогичном расщеплению электронных термов атома в кристаллическом