сомнения в том, что вместе с ростом объема памяти и скорости счета ЭВМ наряду с усовершенствованием самих методов и алгоритмов трудоемкость неэмпирических методов будет непрерывно убывать, а их точность и адэкватность расти. Поэтому сегодняшние неэмпирические методы создают ту базу, на основе которой будут вестись массовые расчеты ближайшего будушего. Помимо этого они являются также основой для усовершенствования существующих и создания новых полуэмпирических и полуколичественных методов, сохраняя по отношению к последним контрольный характер.

Сравнение с теорией кристаллического поля

При сравнении метода МО ЛКАО с теорией кристаллического поля видно, что в ряде случаев они приводят к аналогичным, внешне очень сходным результатам и прежде всеГо -к совпадению качественных характеристик: симметрии молекулярных термов, их мультиплетности, взаимного расположения и др., для которых основные результаты теории кристаллического поля могут быть получены из более общих результатов метода МО ЛКАО, если для разрыхляющих орбиталей параметр ковалентности [у в формуле (V. 26)] положить равным нулю. В этом отношении любопытна дискуссия об эффективности приближения теории кристаллического поля для координационных систем, излагаемая здесь вкратце (более детальные ссылки см. [9, с. 91]).

Первые расчеты параметр*а расщепления Д в приближении теории кристаллического поля с лигандами - точечными ионами и диполями, - выполненные Ван Флеком и Полдером для иона Сг+ в окружении шести молекул воды, дали результаты, качественно согласующиеся с экспериментальными данными. Клейнер [230] попытался улучшить расчеты, отказавшись от предположения о точечности зарядов лигандов и учитывая их размазанность в пространстве посредством лигандных функций (но, по-прежнему, без учета ковалентности). Но результаты при этом настолько ухудшаются, что А становится отрицательным (порядок следования уровней меняется на обратный).

Дальнейший вклад в выяснение ситуации внесли Танабе и Сугано [230]. Они учли, что при делокализации электронов лигандов надо провести ортогонализацию волновых функций центрального иона к волновым функциям лигандов электронов, что существенно исправляет результаты. Филипс [230] показал, что влияние орто-гонализации- равносильно появлению дополнительного члена отталкивания от лигандов, а учет делокализации электронов (отказ от точечности поля) лигандов эквивалентен некоторому дополнительному притяжению. При этом догГолнительные члены отталкивания и притяжения приближенно компенсируются и точечная модель кристаллического поля оказывается хорошим приближением.

Дальнейший анализ и более точные расчеты были выполнены авторами работ [102, 103, 202] и др. Сугано и Шульман [202]

в приближении МО ЛКАО рассчитали вклады ковалентности на примере координационной системы [NiFe] * кристалла KNiFa. Свои результаты они интерпретировали так, что основной вклад в величину параметра расщепления А вносит учет ковалентности. Однако более глубокий анализ этой системы [102] показал, что такая трактовка некорректна и непосредственный вклад ковалентности не превышает 10-20%.

Таким образом, можно утверждать, что в ряде случаев модель кристаллического поля с лигандами - точечными зарядами или диполями - оказывается разумной. При этом необходимо иметь в виду, что по самой постановке вопроса ряд задач не может быть рассмотрен в такой модели. Это относится прежде всего к эффектам, связанным с переносом спиновой плотности в любых системах, а также к анализу электронного распределения и свойств ряда сложных координационных систем (металлоорганических, хелатных, сэндвичевых и других), для которых существенны детали строения лигандов, не учитываемые аппроксимацией электростатического влияния.

В каком-то смысле промежуточным между методом МО ЛКАО и теорией кристаллического поля можно считать метод углового перекрывания (раздел V. 3), позволяющий, загнав ковалент-ность в параметры, изучить зависимость относительных свойств систем разной геометрии от координат точек лигандов.

V.6. Х -МЕТОД СЛЭТЕРА-ДЖОНСОНА

Новый метод расчета электронного строения многоатомных систем, получивший распространение за последние несколько лет (его полное название: Х-метод самосогласованного поля и рассеянных волн* -ССП -Ха - РВ), как и метод МО ЛКАО основан на одноэлектроииом приближении и на методе самосогласованного поля Хартри -Фока. Однако, в отличие от метода МО ЛКАО в нем отказываются от представления МО в виде ЛКАО, заменив его другим подходом. Последний состоит в том, что МО ищут в виде самосогласованного суммарного решения, надлежащим образом сшитого из приближенных решений, полученных отдельно для областей вблизи ядер, между ними и вне их, предполагая некоторое усредненное распределение плотности электронов в каждой из них.

В настоящее время известно значительное число конкретных расчетов, проведенных этим методом, которые демонстрируют ряд его преимуществ перед методами МО ЛКАО, и в первую очередь резкое уменьшение (по словам авторов - на два порядка) затрат машинного времени, необходимого для расчета многоатомной системы. Основными авторами метода являются Слэтер и Джонсон, его главные особенности и детали изложены в ряде обзорных и основополагающих статей [231-236].

* В литературе ня английском языке: Self Consistent Field Х -Scattered Wave Method (SCF - Хц - SW).

Рассмотрим многоатомную систему - комплекс переходного металла (или любую другую произвольно выбранную группу атомов вещества), или кристаллическую рещетку. В духе одноэлектронного приближения предположим, что каждому электрону можно поставить в соответствие одноэлектронное состояние, характеризующееся волновой функцией его координат и спина Ц)}{г),

и определим электронную плотность р(г) как сумму плотностей электронов со спинами V2 и -V2 (обозначаемых дополнительными стрелками вверх и вниз)

~ (V.99)

рФ(г)=2 /ф/ИР P(r) = pt()--P4-(T)

(V. 100)

где tij - числа заполнения одноэлектронных состояний 9j(r); для свободного атома rij равно О или 1.

В этих обозначениях выражение для полной энергии системы принимает вид (без энергии взаимодействия между ядрами)

Ях = X! г 5 ф! (О Я°ф (О rfT -Ь1 е= 5 р (1) р (2) J- dr, dx +

+ Т S [Pt (1) Uxi) + PiO) X (1)] (V. 101)

Здесь /?° - гамильтониан остова (11.38).- оператор кинетической энергии электрона и его взаимодействия с ядрами: 6x >b и Ux-соответствующие обменные потенциалы, различные для спинов вверх и спинов вниз, так как обменное взаимодействие отлично от нуля только для электронов с одинаковым направлением спина.

Во второй член (V. 101) -чисто кулоновское отталкивание между электронами (вычисляемое классически как отталкивание двух электронных облаков)-входит также энергия взаимодействия электрона с самим собой, которая, однако, сокращается с соответствующей частью третьего члена - обменного взаимодействия [вполне аналогично уравнению Хартри-Фока (11.41)].

Уравнение (V. 101) -точная запись полной энергии системы в одноэлектронном приближении при условии, что вместо х (1) подставляют точный потенциал обменного взаимодействия. Название метода обязано приближенному выбору этого потенциала. Из статистической модели атома известно, что обменный потенциал можно представить пропорциональным плотности электронов в степени Vs. Слэтер [231] предложил выбрать этот потенциал в виде

где (х, - некоторый параметр (см. ниже). Для Ux выражение аналогично. Представление обменного потенциала в форме (V. 102) - первое существенное приближение Х -метода.

Варьируя энергию (V. 101) по ф((г) при фиксированных щ [с учетом (V. 102)], мы найдем уравнения, которым должны подчиняться функции фi(г), соответствующие минимуму энергии системы

Ф,(0 = е,Ф,() (V.103)

-iir+cir)+Vxj)

где Vcir) - классический кулоновский потенциал от всех электронов и ядер;

Vx, (г) = (2/3) Ux tr) и Fx + fr) = (2/3) Ux (г) - обменные по-

тенциалы, различные для разных групп электронов.

Уравнения (V. 103) в принципе не отличаются от уравнений Хартри -Фока (П.41) [а с выбором обменного потенциала по (V. 102] они ближе к уравнениям Хартри (11.37)]. Если теперь

искать фг(г) в виде ЛКАО и минимизировать полную энергию по коэффициентам ЛКАО, то мы придем снова к упрощенному ва-пианту метода МО ЛКАО. В отличие от последнего в Хд-методе, начиная с этого места, процедура рещения уравнения (V. 103) совсем иная.

Окружим каждый атом некоторой сферой радиуса R с центром в ядре, так чтобы сферы различных атомов соприкасались (в необходимых случаях, например, для неполеленной пары, вводят еще дополнительные промежуточные сферы ), а всю систему - большой сферой, охватывающей все атомы, и разделим все пространство на три области (рис. V. 8):

I - область внутриатомных сфер; И - область между атомными сферами, но внутри большой сферы;

1П-область вне большой сферы.

Второе существенное приближение Х -метода заключается в том, что уравнение (V. 103) решается отдельно для областей I, II и III и затем эти решения сшиваются. При этом потенциал Vc + Vx в области I берется средним сферическим симметричным (по каждой сфере), в области II - постоянным, усредненным по объему области, а в области III - также сферически симметричным (относительно выбранного центра системы, вокруг которого проведена большая сфера).

С такими потенциалами решения уравнения (V. 103) в областях I и III получаются в виде водородоподобных функций типа (II. 1) с радиальной частью, определяемой численным интегрированием, а в области II - в аналитических специальных функциях, которые можно интерпретировать как расходящиеся, сходящиеся

и стоячие сферические волны, отраженные от атомных областей и области внешней сферы. Для сшивания этих решений искомую

q>i{r) разлагают по системе решений в каждойобласти и затем из

условия непрерывности ((ii{r) и ее первых производных находят соотношения между коэффициентами разложения, которые имеют вид некоторой совокупности секулярных уравнений. Последние дают нетривиальные решения только при определенных значениях

по щ [231, 234, 237]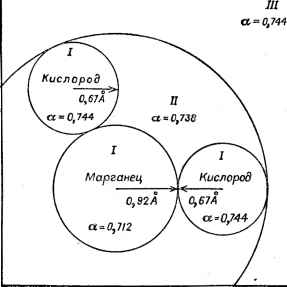

Рис. V.8. Разделение комплекса МпО на три области и значения параметра а при расчете его электронного строения по методу ССП-Х -РВ [235]:

1-область внутри атомных сфер; П-область между атомными сферами внутри большой сферй;

большой область вне боль-

шой сферы. 1 а=10~ м.

энергии е, которые и есть собственные значения одноэлектронного

состояния фг(). Этз процсдурз сшивания решений получила название метода многократно рассеянных волн.

Зная функции фг(), можно вычислить по формулам (V. 99)

и (V. 100) электронные плотности р(г). РИ) и р(г) и с их помощью определить потенциалы Ус (используя классическое электростатическое уравнение Пуассона) и Ух [по формуле (V. 102)], усреднить последние (сферически- в областях 1 и 111 и объемно в области II), затем решать уравнение (V. 103) по соответствующим областям, методом рассеянных волн сшить найденные решения, определив при этом новое значение ф(г) и соответствующий вид е и т. д. до полного самосогласования.

Существенно, что в Х -методе соотношение между одноэлектронной энергией ei и полной энергией системы Е иное, че*! в обычном методе Хартри - Фока. Действительно, в Х -методе одноэлектронная энергия е равна производной от полной энергии

.х

(Эп,

(V. 104)

В то время как в методе Хартри - Фока е,- равна разности энергий двух состояний, отличающихся соответствующими числами заполнения:

гх-Ф = х-Ф (п = 1) - Ех-ф (п; = о) (V. 105)

Представление (V. 104) с учетом нелинейной зависимости Е от щ имеет ряд преимуществ перед (V. 105). В частности, для вычисления энергии одноэлектронного перехода с изменением чисел заполнения Пг-щ-!, mj-vmi-fl, на основе (V. 104), нет необходимости рассчитывать полные энергии двух состояний, начального и конечного, - достаточно вычислить их в так называемом промежуточном состоянии cnt = ni--j и тг = т,-Ьг [231].

Некоторые пояснения требуют выбор параметров а в обменном потенциале t/x по (V. 102) и радиуса сферы вокруг атомов. Первоначальное значение а= 1, предложенное Слэтером [238] для атомных расчетов, было затем исправлено Гашпаром [239], который показал, что а 2/3. Более точные значения а можно получить, например, из сравнения полной энергии основного состояния соответствующего атома, вычисленной с потенциалом (V. 102), с более точным значением, полученным по методу Хартри - Фока. Таким путем были протабулированы значения а для всех атомов от водорода до ниобия [240] (возможны и другие методы оценки а [234, 237]; все они получаются довольно близкими и промежуточными между значениями Слэтера а=1 и Гашпара а = 2/3). В области II а можно взять средним по сферам области 1, а в области III близким к а для внешних атомов.

Радиусы сфер области I Rf предлагается выбрать с учетом межатомных расстояний так, чтобы на границе между двумя соприкасающимися атомными сферами потенциал не имел разрыва. В случае сложного соединения здесь остается некоторый произвол, хотя результаты расчетов не зависят сильно от малых изменений R{. В области III могут быть дополнительные граничные условия (например, для заряженного кластера в кристалле можно ввести дополнительный, тоже усредненный потенциал ионов окружения в кристаллической решетке).

С увеличением расстояния между атомами общее решение в Х -методе будет приближаться к сумме решений для системы невзаимодействующих атомов [231]. В отличие от этого метод МО ЛКАО дает решения, которые на больших межатомных расстояниях включают с одинаковым весом атомные и ионные состояния (например, для молекулы водорода - состояния H-j-H и H+-I-H-), что является результатом недооценки электронных корреляций в этом методе. Особенно это относится к той ее части, которая обязана локальному взаимодействию электронов