Неэмпирические расчеты пятикоординированных комплексов CuCls , Cu(H20)5 и Fe(CO)5 [175] в конфигурациях квадратной пирамиды и треугольной бипирамиды показали, что энергии этих jpyx конфигураций очень близки (разность составляет величину порядка десятка кДж/моль), что объясняет их стереохимическую мягкость .

Энергии связей определены только в некоторых из перечисленных случаев. Сравнивать эти цифры с экспериментом трудно, так как иногда не совсем ясно, что следует считать связывающимися продуктами - нейтральные лиганды, их ионы, отдельные атомы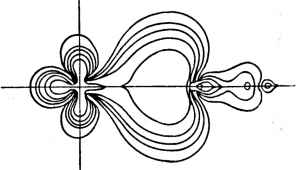

Рис. V. 7. Кривые распределения электронного облака вдоль связи Ni-С в соединении Ni (CN)~ по результатам неэмпирического расчета [164].

И Т. Д. Например, рассчитанная энергия связи в №(С0)4 по отношению к лигандам и нейтральному атому Ni в синглетном состоянии 5 360 кДж/моль (86 ккал/моль) [164], а в другом расчете [161] по отношению к триплетному состоянию нейтрального никеля получается 604 кДж/моль (144 ккал/моль) [экспериментальное значение в газовой фазе - 587 кДж/моль (140ккал/моль)]. В случае Ni(CN) энергия связи [2547 кДж/моль (608 ккал/моль)] рассчитана по отношению к распаду на ионы Ni и CN, так 4jo большая часть этой энергии падает на электростатическое взаимодействие ионов [164], и поэтому ее нельзя сравнивать с экспериментальной оценкой -180 кДж/моль (43 ккал/моль) для сольва-тированных ионов.

Для перманганат-иона MnOI энергия связи получается отрицательной и существование этого иона в кристаллах можно объяснить либо стабилизацией его в кристаллической решетке, либо несовершенством расчета (за счет неполноты базиса и неучета эффектов корреляции). Интересно отметить, что энергия связи в ионе Ag(C2H4)+ 117 кДж/моль (28 ккал/моль) большей частью [63 кДж/моль (15 ккал/моль)] приходится на зарядовую поляризацию, а остальное -на электронную делокализацию и ковалент-ность [173].

Существенные закономерности удалось выявить при анализе потенциалов ионизации и их связи с порядком расположения рассчитанных одноэлектронных уровней в системе. Согласно теореме Купманса (раздел V. 3), энергия ионизации электрона из данного одноэлекгронного состояния молекулы равна взятой с обратным знаком энергии соответствующей МО. Поэтому последовательность потенциалов ионизации (или расположения пиков в фотоэлектронных спектрах, см. главу VII) должна следовать за последовательностью расположения уровней МО сверху вниз. Эта закономерность действительно иногда наблюдается, например, для упомянутого Ni(C0)4 [161, 164]. Однако для большинства случаев ее нет. Это относится прежде всего к металлорганическим соединениям и комплексным анионам. Например, для ферроцена расчет дает следующий порядок расположения -уровней МО [170]:

fli {3d) < e2g {а - Ср) ~ Оги { - Ср) ~ ги (f - Ср) < < e2g{3d) <eig{n - Cp) ~ е, (я - Ср).

Экспериментально же установленный по фотоэлектронным спектрам порядок следования потенциалов ионизации / иной [176].

Если отказаться от приближенной теоремы Купманса, то потенциалы ионизации необходимо считать разностью энергий исходного состояния молекулы Fe(Cp)2 и конечного состояния иона Fe(Cp+)2. Проведенные таким образом расчеты [170] дают следующий порядок следования /

He2g) < I {aig) < I (е, ) < / (е,)

находящийся в полном согласии с экспериментальными данными. Эти и другие расчеты показали, что широко используемая теорема Купманса, вообще говоря, может привести к ошибочной интерпрета111и. Как и в примере с ферроценом в комплексных анионах очень часто верхними заполненными оказываются уровни лигандов (р-уровни галогенов; зт-уровни CN и т. д.), в то время как первый потенциал ионизации, рассчитанный как разность энергий основного состояния исходного и ионизованного комплексов, соответствует удалению З-электрона металла в согласии с экспериментальными данными.

Особенно интересны для химии получаемые из расчета детали электронного строения, позволяющие оценить переносы и перераспределения зарядов при комплексообразовании. Эти данные можно сравнить с получаемыми из экспериментов по сверхтонкой структуре спектров ЭПР и ЯМР. Например, расчеты магнитного экранирования протонов в комплексе ТсНд оказались в хорошем согласии с экспериментальными данными и позволяют заключить, что все водороды находятся в почти идентичных условиях электронного окружения [169]. Большое число приложений результатов расчетов относится к электронным спектрам (глава VII).

Гораздо больше расчетов выполнено полуэмпирическими (МВГ, НДП) и полуколичественными (ПК) методами. Под

последними понимается рутановский расчет методом ССП МО, в который введены существенные упрощения с целью сокращения объема расчетов, основанные, например, на разложениях типа Рюден-берга [114] или Маликена [134]* (или неэмпирические варианты НДП). В литературе встречаются разные варианты ПК расчетов. При этом имеется в виду, что эмпирические параметры (кроме параметров геометрии системы и зарядов разных ядер) обычно не используются. Примером полуколичественных расчетов могут служить ранние расчеты ферроцена [177] и недавние расчеты фторидов, в основном, неметаллов, проведенные М. Е. Дяткиной с сотрудниками [178, с. 19-26].

В отличие от полуколичественных в полуэмпирических методах, описанных выше, используются эмпирические параметры, главным образом, спектроскопические данные для атомов, входящих в систему. Ниже приведено весьма краткое обсуждение некоторых результатов таких расчетов, в целом представляющих лишь очень малую часть той информации об электронном строении соединений, которую можно получить ш этих работ.

В серии расчетов гексагидратов двухвалентных и трехвалентных металлов [179] методом ППДП исследована их возможная геометрия и показано, в частности, что Си(Н20)2+, Сг(Н20)+ Мп(Н20)+, имеющие в основном состоянии конфигурации правильного октаэдра, двухкратно вырожденный электронный £-терм, имеют минимумы энергии в тетрагонально искаженной конфигурации, в полном соответствии с предсказаниями эффекта Яна - Теллера (глава VI). В другом расчете [180] определена равновесная конфигурация CuFg , которая также, в подтверждение эффекта Яна-Теллера, оказалась тетрагонально искаженной (с разностью длин связей ~0,2А). Этот результат подтверждается также в работе [181], в -которой методом ППДП рассчитана серия гексафторидов переходных металлов. Расчеты величины ян-телле-ровского искажения октаэдрических комплексов методом МВГ приведены также в работе [182]. Полуэмпирические расчеты статических искажений в тетраэдрических комплексах см. в работе [183].

Результаты серии расчетов карбонилов металлов сведена в табл. V. 10 (большая часть данных этой таблицы заимствована из обзора [131]). Одно из следствий этих расчетов состоит в том, что появляется возможность оценки относительных вкладов п-и а-типов как в образование связи металл - лиганд, так и в изменение связи С-О при координировании к металлу. Из результатов расчетов изоэлектронной серии [190] Мп(СОб)*, Mn(C0)5CN, Mn(CN)5C0 и Mn(CN)g можно заключить, что карбонильная группа участвует в связи, главным образом, своей возбужденной я*-орбиталью. Участие же цианидной группы в связи зависит от

Разложение Рюдеиберга [114] является обобщением формулы Маликена (V.58) или (V. 65), в котором используется точное разложение орбитали данного атома, по ортогональной системе орбиталей другого атома,

* в скобках указан ее тип симметрии; ХФР-Хартри -Фок-Рутаав.

Некоторые результаты расчета карбонилов переходных металлов полуколичественными (ПК) и полуэмпнрнческнмн методами (типа МВГ)

числа соседей-карбоиилов: при преобладании CN-rpynn их участие в связи приводит главным образом к изменению их зт-связей, а при преобладании карбонилов в координационной сфере меняются как а-, так и зт-связи этой группы.

Хорошее согласие рассчитанных полуколичественным методом [196] данных с опытными, полученными из результатов фотоэлектронной спектроскопии, найдено для энергии верхних заполненных МО в серии карбонилов марганца общей формулы Мп(СО)бЬ, где L -Н, С1, Вг, 1 (табл. V. 11). В расчетах карбонильных кластеров металлов, например, типа Мег (СО) ю, где Мег -Мпг, Тсг, Кег, MnRe, и других [191; 192, 197], выявлено происхождение сильной связи Me-Me и Me данного фрагмента с группой СО другого.

Таблица V. 11

Сравнение рассчитанных н наблюдаемых.энергий внешних заполненных МО для ряда карбонилов типа Mn(c0)5L [196]

Расчет двуядерных карбоксилатов меди [198] дал интересные сведения о происхождении связи между моноядерными группировками и ее ВЛИЯНИИ на наблюдаемые магнитные свойства соединений.

Оказалось, в частности, что в отличие от упомянутых карбонилов металлов предположенная ранее непосредственная связь Си-Си весьма незначительна, и что обменное взаимодействие между спинами неспаренных электронов ионов Си* осуществляется через кислородные мостики.

Многие расчеты посвящены фторидам переходных металлов:

TiFi . VF, CrFi , MnFr, МпЕГ. VeVt, FeF, СоГГ. CoF.

NiFe и CuFe ; проведены они полуэмпирическим методом типа МВГ [199], методами ППДП [181] и МЦНДП [200], а также неэмпирически [163, 201]. В большинстве из них главное внимание

уделено получению правильного значения разности энергий основного и первого электронно-возбужденного состояния, по смыслу совпадающей с введенным в теории кристаллического поля основным параметром расщепления Д = lODg. Ниже приведены (весьма поучительные) результаты ряда неэмпирических расчетов этой величины, проведенных для одного и того же объекта - с различными упрощениями процедуры ССП МО ЛКАО (либо с различными базисами), а также (для сравнения) в приближении МВГ и в модели теории кристаллического поля (ТКП) с точечными зарядами:

Автор

Сугано. Шульман [202] Ватсон, Фримен [102] . Хаббард с сотр. [203] . Ричардсон с сотр. [201]

Ричардсон с сотр. [204] . Элис, Фримен, Рос [205] Глэдни, Вейяр [206] . . Московиц с сотр. [163] . Офенхартц [207 .... Приближение Т Ш [163] Баш с сотр. (МВГ) [147] Эксперимент [208] . . .

Д= 10 D, см

6350 2800 5400 7126 7922 7210 10500 4670 6089 7250 1512 7300 7250

Эти данные показывают, что (за исключением случая ТКП) все расчеты в основном правильно схватывают сущность явления и дают правильный порядок величины А, а в некоторых случаях (в том числе методом МВГ) получено весьма удовлетворительное количественное согласие с экспериментом.

В этих расчетах попутно решался ряд методических задач, что позволило лучше понять роль и место приближения теории кристаллического поля в анализе свойств таких комплексов (см. ниже).

В полуколичественных расчетах ряда тетраэдрических (TiCU, VCI4, FeCU, MhCir, FeCir, C0CI4 , NiCl ) и октаэдрических (TiCle , VCle. CrCli , FeCle) хлоркомплексов [209] получено удовлетворительное качественное согласие между заселенностями связей М-С1 и соответствующей частотой колебаний. Аналогичные расчеты серии комплексов MCle (где М - Re, Os, 1г, Pt) методом МВГ проведены в работе [210].

Большой интерес для приложений представляют рассчитанные заряды на ц. а. Для них в большинстве случаев получаются разумные значения (см. табл. V.9, V. 10 и V. 12), которые качественно согласуются с экспериментальными данными, например, по /С-краю поглощения рентгеновых лучей. При анализе этих величин следует, однако, иметь в виду, что используемое выше определение эффективного заряда на атоме по Маликену [141] [формула (V. 77)] не совпадает с действительным распределением заряда вблизи данного атома, особенно в случае переходных металлов