на отдельные фрагменты и последовательному расчету каждого из них - пофрагментный расчет.

Проблема подобных расчетов особенно важна еще и потому, что с увеличением числа функций в базисе метода МО ЛКАО затраты машинного времени т очень быстро возрастают (т и расчеты больших молекул без деления на фрагменты становятся экономически неприемлемыми.

Из известных методов пофрагментных расчетов отметим здесь предложенный недавно [154], главным образом, для неэмпирических расчетов органических молекул с заполненными оболочками. Суть- этого метода состоит в том, что предварительно рассчитывают небольшие молекулы - аналоги фрагментов искомой большой молекулы, а затем используют полученные татим образом функции как базис метода МО ЛКАО для полного расчета большой молекулы. Например, для расчета молекулы этана [155] сначала проводят неэмпирический расчет для молекулы метана, а затем ищут решение для молекулы этана в виде линейной комбинации решений для двух молекул метана (предполагая, что удаление двух атомов водорода при образовании этана из метана компенсируется в базисных функциях образованием связи С-С). При этом расчеты фрагментов проводят с использованием плавающих сферических гауссовых функций* [156], для которых варьируется не только показатель экспоненты, но и их местоположение в пространстве. Автору [154] удалось распространить этот метод на ряд больших органических систем, однако к координационным соединениям он в его нынешней форме едва ли применим.

Анализу проблемы пофрагментных расчетов, в том числе (и особенно) координационных соединений, посвящена работа [157].

Пусть молекулярная система формально разделена на два фрагмента. Очевидно, что последовательный расчет фрагментов по схеме МО ЛКАО вместо одновременного расчета системы в целом возможен в том случае, если удается привести матрицу секулярного уравнения (V. 8) к квазидиагональному виду. Тогда на ее Диагонали расположатся две квадратные матрицы, так что ее детерминант станет равным произведению двух детерминантов меньшего порядка. В поисках условий, при которых это возможно, необходимо, в первую очередь, проанализировать роль атомов, расположенных на границе между фрагментами - пограничных атомов ПА, так как остальные атомы из разных фрагментов, как предполагается, пренебрежимо слабо взаимодействуют между собой из-за большого расстояния между ними. Допустим, что имеется всего один ПА, который образует с каждым из фрагментов только а-связи (рис. V. 6). Обозначим а-функции, направленные к двум фрагментам, через а, и as, а непосредственно перекрывающиеся с ними а-функции соседних атомов в фрагментах - через ai и ак.

* В литературе на английском языке: Floating Spherical Gaussian Orbitals (FSQO).

Для простоты последующих рассуждений предположим, что задача МО ЛКАО решается в ортогонализованном базисе (т. е. атомные функции выбраны ортогональными между собой и все Sij = 0); это же относится, естественно, и к выделенным четырем функциям. Тогда в секулярном уравнении (V. 8) соответствующая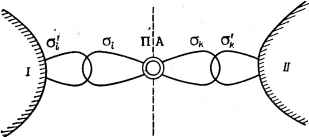

Рис. V.6. Пограничный атом (ПА) и четыре о-состоя-ния, наиболее активные во взаимодействии фрагментов.

взаимодействиям ПА часть, представленная функциями, имеет вид, выделенный пунктиром:

этими четырьмя

(V.92)

Очевидно, что упомянутый выше квазидиагональный вид секулярного уравнения будет достигнут, если

(V.93)

Оказывается [157], что это условие выполняется точно только тогда, когда а-связи ПА с фрагментами осуществляется чистыми (негибридными) р-, d- или /-функциями (например, если о есть рзс-фупкция, а Oft - Ру или d-функция). Эти случаи довольно редки и нуждаются в дополнительном обосновании отсутствия s-вклада. Во всех остальных вариантах межфрагментные резонансные интегралы Hiu пропорциональны разностям кулоновских интегралов состояний, участвующих в гибридизации. Для гибрид-пых 5р2-функций, например, Н{Нss -Н(в то время как

внутрифрагментный интеграл Нц - {Hss + Нрр); см. таблицу в работе [157]).

Из Этого примера видно, что межфрагментные интегралы, составляя доли разности значений интегралов типа Яц для гибри-дизируемых атомных состояний ПА, существенно меньше соответствующих внутрифрагментных интегралов, равных суммам таких же интегралов. Обычно наибольший по абсолютному значению межфрагментный интеграл Hih выражается через атомные кулоновские интегралы Я, которые в свою очередь могут быть определены, например, из эмпирических данных. При этом они оказываются существенно зависящими от валентного состояния атома и заряда на нем. Например, с изменением заряда на атоме переходного металла в небольших пределах разность Hsis - Наы меняет знак, проходя через нуль (табл. V. 6). Сами же кулоновские и обменные интегралы могут быть довольно значительными. Поэтому вполне возможны условия, когда межфрагментные интегралы по абсолютному значению существенно меньше внутрифрагментных (см. также обсуждение в [24]).

Из сказанного непосредственно вытекает обоснование выбранному способу разделения системы на фрагменты, при котором ПА участвует частью орбиталей в одном фрагменте и частью в другом. Легко также видеть, что, если ПА обладает активной п-орби-талью, образующей одного порядка связи с обеими фрагментами, такое выделение фрагментов стало бы-невозможным, ибо в любой комбинации межфрагментные интегралы были бы того же порядка, что и внутрифрагментные. Этот вывод подтверждается непосредственным расчетом [158].

3 любом из рассмотренных выше случаев без дополнительного исследования остается неясным, какой малости должны быть межфрагментные интегралы, для того чтобы ими можно было пренебречь в секулярном уравнении, и какое влияние на решение задачи МО ЛКАО оказывает такое пренебрежение частью матричных элементов. Для выяснения этого важного вопроса можно воспользоваться непосредственно теоремой Гершгорина о локализации характеристических чисел матрицы [159].

Применительно к рассматриваемому нами случаю эрмитово-сопряженных матриц эта теорема гласит, что область локализации корней секулярного уравнения (V. 8) порядка п удовлетворяет следующим неравенствам (на комплексной плоскости - круги Гершгорина ):

Я -е< (t = 1.2.....п) (V.94)

Отсюда видно, что область локализации энергий МО относительно диагонального элемента Нц определяется суммой абсолютных значений всех недиагональных элементов Hij данной t-ой строки. Поэтому пренебрежение одним элементом Hih (его отбра-

сывание) сужает две области локализации корней [радиусы i-ro и k-TO кругов Гершгорина в (V. 94)], приближая соответствующие энергии МО к атомным значениям Нц и Hhh- При этом эффект определяется сравнением с суммой всех остальных значений \Hij\ (или Яь). Отсюда вытекает обоснованный критерий малого влияния на уровни энергии МО отбрасываемых межфрагментных интегралов: они должны быть значительно меньше соответствующих сумм внутрифрагментных интегралов с участием рассматриваемого состояния ПА.

После отбрасывания межфрагментных интегралов и расчета системы пофрагментно можно попытаться учесть влияние отброшенных малых членов методами теории возмущений. Для этого предположим сначала, что образованные с участием а-функции ПА МО в каждом из фрагментов достаточно сильно разнесены по энергиям, т. е. в непосредственной близости с существенным взаимодействием между ними оказываются только два уровня

и 8 от I до II фрагментов. Обозначим .коэффициенты ЛКАО при функциях ПА для этих МО с и сД (для простоты все функции и матричные элементы предполагаем действительными). Тогда секулярное уравнение возмущения этих двух уровней с учетом ненулевого значения Hih имеет вид

1 11 и

(V.95)

откуда непосредственно находятся возмущенные уровни энергии.

Обратим внимание на то обстоятельство, что смещения уровней определяются не абсолютным значением ранее отброшенного матричного элемента Hih, а выражением Рав1Ягь, где

Ра(3 = 144*1

(V.96)

- параметр, отражающий долю участия рассматриваемых функций ПА во взаимодействующих МО разных фрагментов. Так как р Г (причем знак равенства относится к практически неинтересному случаю cjj,-= с = 1, когда в фрагментах не образуются МО с участием функций ПА), то взаимодействие состояний ПА в результате образования МО в фрагментах уменьшается (подавляется), причем это уменьшение (подавление) тем больше, чем больше делокализации состояний ПА в рассматриваемых МО. Отсюда следует, что образование МО с участием возможно большего числа атомов в фрагментах уменьшает ошибки пофрагментного расчета. Параметр р по (V. 96) для краткости удобно назвать параметром подавления.

Если невозможно выделить только две взаимодействующие орбитали двух фрагментов, секулярное уравнение теории возмущений, естественно, усложняется. Но и в этом случае можно получить оценку локализации энергий МО, подобную (V. 94) [157]:

1 еа - е I < V I ciHik I [v = 2-/= (ViT+T - \)Ц (V. 97)

Отсюда Ёйдно, что смещение энергии а-ой МО под воздействием соседнего фрагмента определяется величиной, пропорциональной Cai- Как и для приведенного выше двухуровневого случая, уменьшению влияния межфрагментного взаимодействия способствует делокализация состояния ПА в МО фрагмента, уменьшающая численное значение коэффициента ЛКАО с,-.

В работе [157] был также предложен метод двойного самосогласования, в значительной мере устраняющий ошибки пофраг-ментного расчета. В этом методе расчеты фрагментов повторяются несколько раз (иттеративно), каждый раз с изменением полного заряда на них (из-за его перекачки через ПА) до полного межфрагментного самосогласования.

V. Б. ВОЗМОЖНОСТИ И ОГРАНИЧЕНИЯ МЕТОДОВ МО ЛКАО

Расчеты злектронного строения координационных систем

Начнем этот раздел с краткого обзора результативной части методов МО ЛКАО в применении к координационным соединениям на примерах конкретных расчетов электронного строения. Наиболее сложны неэмпирические аЬ initios расчеты в приближении ССП МО ЛКАО (метод Рутаана), применение которых к координационным соединениям стали возможны лишь в последние годы благодаря растущей мощности ЭВМ. В табл. V. 9 сведены данные по нескольким известным неэмпирическим расчетам координационных систем (см. обзоры [130-132, 160]). В ней для иллюстрации приведена полная энергия электронов (при фиксированных ядрах), энергия связей (по отношению к металлу в соответствующем состоянии окисления и лигандам или по отношению к составляющим систему атомам), и формальный заряд на центральном атоме, вычисленный по Маликену [141].

Помимо этих данных указанные расчеты позволяют определить детальное распределение электронного облака в соединении (см. для примера рис. V. 7), относительные устойчивости различных конфигураций (там, где проведены расчеты для различных конфигураций), порядок расположения одноэлектронных уровней энергии внешних* электронов, потенциалы ионизации из различных уровней (ожидаемые фотоэлектронные спектры) и сродство к электрону, частоты и вероятности электронных переходов с поглощением или излучением света и др.

Интересны результаты по относительным энергиям конфигурации. Так, для комплекса CUCI4 наиболее устойчива конфигурация сплюснутого тетраэдра Did (сравнивать следует данные табл. V. 9, полученные расчетами с одинаковым базисом) с углом С1-Си-С1 в 120° в согласии с эффектом Яна - Теллера (глава VI), а для тетраэдра NiCl4 высокоспиновое состояние Г, в согласии с экс- периментом (см. также стр. 170) устойчивее низкоспинового состояния Гг [на 272 кДж/моль (на 65 ккал/моль)].

Таблица V.9

Некоторые результаты назмпнрнческнх расчетов коордннацнонных систем

а-в расширенном базисе;

Ь -то.чько валентных оболочек;

с - по отношению к лигандам н металлу;

d -по отношению к N10 в состоянии IS;

е -По OTiioiueiiHro к N10 в состоянии F;

I - по отношению к чтдмам.