при большем числе атомных функций, преобразующихся по данному типу симметрии, степень секулярного уравнения и число образуемых МО повышаются, что существенно ограничивает возможности наглядного толкования. Однако и в этом случае деление МО на связывающие, разрыхляющие и несвязывающне производится по положению соответствующих им энергии относительно чисто атомных значений, а квадраты коэффициентов при ЛКАО определяют относительное распределение электронного облака на данной МО.

Случай слабой ковЬлентности. Метод углового перекрывания

В расчетах молекулярных систем, особенно координационных соединений, часто встречается случай так называемой слабой ковалентности, когда отношение Hoil{Hn - Hqq) и S малы по сравнению с единицей. В этом случае, пренебрегая квадратами этих величин, можно получить из формулы (V. 24) следующие выражения;

р (Яр! - ЯроСр!)

£l /Уро--тг--77-

Л и - Л 00

(V.25)

Для волновых функций МО удобна запись в форме

2 = ЯИФ1-Чо) где и Ла - константы нормировки:

ЛГ,= [1+у + 2уСо,] 2 \

(У.2в)

(V.27)

Из условия ортогональности функций (V. 26) легко получить соотношение между константами у и Я,*:

, Y-fCp,

1 +YGp,

В принятом выше приближении можно также получить:

Hoi - HmGoi

Нц - Но

= Y + Co

(V.28)

(V.29)

Запись волновых функций в форме (V. 26), позволяет просто истолковывать постоянные у и Я,. При у = О Ч ] = -фо и связывающий электрон находится исключительно на ц. а. С другой стороны, точное значение у = 0 возможно лишь при Яо1 = Gqi = О, так что

* Не следует смешивать константу ковалентности Я с константой спин-орбитального взаимодействия, которая обозначается той же буквой.

по уравнению (V.29) Я = О и, следовательно, 42 = Фи т. е. разрыхляющий электрон находится исключительно на лигандах. В этом случае, таким образом, МО являются несвязывающими и связь носит чисто ионный характер.

При уфО и Я, =/= О электроны связи коллективизируются, причем при Y = = 1 связывающий электрон с одинаковой вероятностью включает в себя орбиталь ц. а. ij3o и орбиталь лигандов Ф, в этом случае связь, осуществляемую на этой МО, можно считать чисто ковалентной. Отсюда следует, что константы у (для связывающей МО) и к (для разрыхляющей) могут служить мерой ковалентности связи.

Заметим, что при 0<у<1 кфу и, следовательно, степень ковалентности на связывающих и разрыхляющих орбигалях различны. При этом для Goi > О Я > Y и Л2 > Ль так что для связывающей МО вероятности нахождения электрона на ц. а. (определяемая величиной Л) и лигандах (Лу всегда меньше, чем

соответственно на лигандах {nI) и ц. а. (л1я) для разрыхляющей МО. Это объясняется тем, что в случае связывающей МО часть электронного облака, определяемая членом 2AiyGoi (облака перекрывания), смещается в область между атомами (в то время как для разрыхляющей МО соответствующий член-2A2Goi <0). Однако изменения энергий на связывающих и разрыхляющих орбиталях, как легко видеть из формул (V.25), в принятом приближении (с точностью до членов более высокого порядка малости) компенсируются, т. е. равны по величине и обратны по знаку.

Слабая ковалентность - весьма частое явление в координационных системах. К ним относятся, например, почти все координационные соединения редкоземельных элементов, для которых активные /-электроны, экранируемые внешними -электронами (как в случае комплексов редкоземельных ионов), образуют слабые ковалентные связи с лигандами. Оказывается, что для этого случая возможно приближение, которое заметно упрощает процедуру нахождения энергий МО и приводит к удобной качественной схеме анализа относительных свойств упомянутых соединений. Это приближение получило название метода углового перекрывания [100].

Воспользуемся для упрощения формул (V. 25) предположением о пропорциональности между Hqi и Goi, лежащим в основе метода Маликена - Вольфсберга - Гельмгольца, (МВГ, см. стр. 149). Согласно формуле (V. 64) с коэффициентом k = 2 Яо1 = (Яоо + Яп) Goi, что после подстановки в (V. 25) позволяет получить

1 = 00 -

2 = 11 +77-г

(V.30)

(V.31)

Отсюда видно, что в рассматриваемом приближении стабилизация связывающей и дестабилизация разрыхляющей МО в

б и. Б. Берсукер

результате образования ковалентной связи пропорциональна квадрату группового интеграла перекрывания. Это утверждение лежит в основе метода углового перекрывания. Именно дестабилизация разрыхляющих d- или /-уровней, относительно легко наблюдаемая в электронных спектрах (особенно в случае /-уровней), может служить критерием ковалентности связи и нефелоксетического эффекта (см. главу VH) на этих уровнях. Однако название метода и его возможности связаны с тем, что интеграл перекрывания Goi представляется в виде произведения радиальной Goi и угловой S частей:

G = g;,h (V.32)

Подставляя это выражение в (V. 31), мы найдем, что энергия дестабилизации разрыхляющих d- или /-электронов Е* = Ei-Hu,

Е* = еВ (V.33)

(V.34)

а индекс Я, введен для различения сг-, я-, б- и т. д. перекрывания металл - лиганд, от которого существенно зависит радиальная часть интеграла перекрывания GJi. Из формулы (V. 33) следует основной вывод метода углового перекрывания: дестабилизация атомных состояний ц. а. вследствие образования ковалентных связей пропорциональна квадрату угловой части интеграла перекрывания.

Так как радиальная часть интеграла перекрывания GSi зависит только от расстояния металл - лиганд (и характера перекрываемых орбиталей), но не от геометрии комплекса, а угловая часть. S сильно зависит от геометрии комплекса, то метод углового перекрывания- удобный способ изучения относительных геометрий комплексов.

В более общей трактовке, которая допускает (из-за низкой симметрии комплекса) перекрывание как типа а, так и двух типов п, л(-1) и л() (симметричное и антисимметричное по отношению к отражению в плоскости, проходящей лерез ось Oz), а также различные типы орбиталей лигандов, перемешивающихся с данной ц. а., формула для энергий дестабилизации d- или /-орбиталей принимает вид

= а Е (с) + *ш [ (-L)] + л (II) Z *01 [ (II)]

i i i

(V.36)

где koi - квадрат угловой части интеграла перекрывания с t-ым лигандом, зависящей от координат последнего. При переходе к групповым интегралам суммы по лигандам пропадают, и

£ (Г) = (о) + я (±) 1 (-L)] + (ю*Ьг [ (11)1 (V. 37)

гг а ч

>

о. о

е 1

м Z m о

3 са о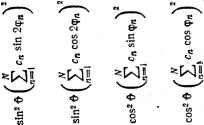

9 a

где or - квадраты угловых частей групповых интегралов перекрывания (для типа симметрии Г), приведенные в табл. V.2. Во .многих случаях фор.мула (V. 33) [только с одни.м членом из (V. 37)] оказывается вполне достаточной для анализа свойств комплексов со слабой ковалентностью по дестабилизация.м разрыхляющих d- или f-орбиталей.

Наиболее вероятные схемы МО

Как уже указывалось ранее (разд. 1.2), трехмерно делокализованные связи координационной системы лучще всего осуществляются при участии d- или /-орбиталей ц. а. Рассмотрим для примера координационную систему, образованную центральным атомом - переходным металлом группы железа (Зй-группы). Его внещние орбитали 3d, is и 4р расположены сравнительно недалеко друг от друга и в валентном (в данном случае положительно заряженном) состоянии образуют следующий порядок расположения энергии уровней: £(3d) < £(4s) < £(4р).

Основные качественные характеристики волновых функций этих орбиталей известны: при прочих равных условиях с лиганд-ными орбиталями лучще всего перекрываются 4s- и 4р-функции и хуже З-функции. Учитывая сделанное выще замечание о зависимости разрыхляющего (или связывающего) характера МО от величины интеграла перекрывания, мы приходим к выводу, что З-орбитали образуют менее связывающие (соответственно, разрыхляющие) МО, чем 4s- и 4р-орбитали.

Рассмотрим конкретную ситуацию октаэдрического комплекса симметрии 0/1. В этом случае 4s-opбитaль преобразуется по Aig (табл. V. 1), 4р-орбитали -по Tiu, а Зй-орбитали образуют две группы: 3rf(fig)-орбитали (dx-y и dzO преобразуются по Eg и, направленные своими гантелями к лигандам, образуют сг-МО, в то время как 3rf(/2g)-орбитали {dxy, dxz и dyz) могут образовать только зх-связи. Вполне очевидно, что 3rf(/2g)-орбитали образуют меньшие интегралы перекрывания с лигандами, чем 3rf(eg)-орбитали. В итоге следует ожидать, что при образовании МО наименьшее расщепление на связывающие и разрыхляющие испытывают jt-MO Tzg-Tma с участием агОрбитали ц. а. Большие расщепления соответствуют МО с участием eg-орбиталей ц. а. и самые большие-МО типа Aig и Tiu с участием его s- и р-орбиталей. Отсюда следует приведенная на рис. V. 3,о наиболее вероятная схема МО для октаэдрической координационной системы симметрии Oh с ц. а. типа переходного металла и лигандами, имеющими только S- и р-активные орбитали. При сравнении легко убедиться, что эта схема полностью соответствует данным табл. V. 1.

Для тетраэдрической системы (симметрии Та) наоборот, 3rf(eg)-орбитали ц. а. хуже перекрываются с лигандными орбиталями, че.м 3d{t2g), так что их роли по сравнению с октаэдрическим комплексом меняются: при образовании МО уровни е-орбиталей расщепляются меньше, чем t2g (рис. V. 3,б).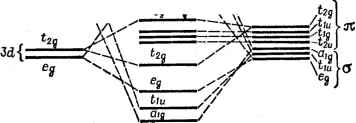

/ ti

орбитали ц.а

e a.

Орбитали лиеанвоВ

Рис. V.3. Наиболре вероятная схема МО для октаэдрического (а) и тетраэдрического {б) комАлексов переходного металла.