ГЛАВА V

МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ (ТЕОРИЯ ПОЛЯ ЛИГАНДОВ)

Молекулярные орбитали основной язык обсуждения химических проблем на электронном уровне.

Двойное название рассматриваемого здесь метода исследования электронного строения координационных систем объясняется тем, что как обобщение теории кристаллического поля, учитывающее эффекты ковалентности, он получил самостоятельное название- теория поля лигандов [1-3]. С другой стороны, метод в целом не отличается от широко известного и наиболее распространенного в квантовой химии и применяемого к любым многоатомным системам метода молекулярных орбиталей МО ЛКАО (хотя в конкретном применении к координационным системам и есть своя специфика). По этой причине в общем плане терминологии квантовой химии название Метод молекулярных орбиталей представляется более обоснованным.

V.I. ОСНОВЫ МЕТОДА

Общие положения

Теория кристаллического поля имеет ограниченную применц-мость, поскольку не позволяет рассмотреть достаточно полно такие комплексы, в которых существенна детальная электронная структура лигандов. Естественно, поэтому, стремление обобщить эту теорию с тем, чтобы по возможности расширить границы ее применимости. В методе МО мы отказываемся от основного ограничивающего предположения теории кристаллического поля, что лиганды можно рассматривать бесструктурно - как неизменные источники электростатического поля, а учитываем их электронные конфигурации и изменение этих конфигураций при комплексообразовании (координировании).

Следовательно, в методе МО учитывают детальную электронную структуру всех входящих в комплекс составных частей. При таком рассмотрении отпадает необходимость делать какие-либо предположения о характере химических связей в комплексе. В отличие от теории кристаллического поля, в которой отдельные атомы или группы атомов в координационном соединении сохраняют Б основном свою индивидуальность и претерпевают лишь нв-

которые изменения (возмущения) в результате взаимодействия с лигандами, в методе МО комплекс, в принципе, рассматривается как единое целое, в котором отдельные атомы или молекулы теряют свои индивидуальные черты.

Например, комплекс [Со(ЫНз)б? в этой теории представляется в виде скелета из 6 ядер азота, 18 ядер водорода и ядра кобальта, в поле которых движутся 84 электрона. Движение каждого электрона в комплексе определяется как положением всех ядер (если считать их в данный момент неподвижными), так и характером движения всех остальных электронов.

Однако нахождение состояний электронов, т. е. точное решение уравнения Шредингера (1.5) для координационного соединения, в настоящее время не представляется возможным, ввиду возникающих на этом пути огромных математических трудностей. Практически приемлемьш здесь остается одноэлектронное приближение, в котором предполагается, что каждый электрон можно рассматривать движущимся независимо в некотором среднем эффективном поле, созданном ядрами и остальными электронами. В этом приближении сложный комплекс описывается одноэлек-тронными состояниями, Ч-облака которых, вообще говоря, простираются вдоль всей системы и поэтому носят название молекулярных орбиталей. Этот метод в общем виде предложен Хундом и Маликеном [96], а его применением к координационным соединениям мы обязаны Ван Флеку, Оргелу, Грифитсу и др. [см. 1-11].

Задача нахождения МО многоатомной системы в общем виде остается довольно сложной. Для ее практического решения необходимо ввести дальнейшие упрощения. Основное из них - приближение ЛКАО, в котором волновая функция молекулярной орбитали представляется в виде линейной комбинации атомных орбиталей:

(V.1)

где /г -число атомов в системе*; я])г - волновые функции соответствующих валентных электронов в атоме I, образующие в совокупности так называемый базис ЛКАО.

Это предположение фактически означает, что орбитальный электрон может находиться с определенной вероятностью (задаваемой константами \Сп\) У каждого из атомов и что вблизи данного атома он движется приблизительно как обычный атомный валентный электрон. Если известны все МО типа (V. 1), то с их помощью можно определить физико-химические свойства системы. , В большинстве случаев в конкретные расчеты по методу МО ЛКАО вводят еще одно упрощение, а именно: игнорируют внутренние оболочки атомов при образовании МО. При этом предполагается, что состояния внутренних электронов атома локализованы

* Равенство числа функций в разложении (V. I) числу атомов в системе необязательно; для более точных расчетов базис ЛКАО берется значительно расширенным, см. ниже.

вблизи отдельных ядер, плохо перекрываются с состояниями соседних атомов и, следовательно, не участвуют непосредственно в образовании МО. Это приближение имеет некоторые экспериментальные обоснования [97]. (Хотя, как это видно из результатов раздела VII. 5, уровни энергии внутренних электронов довольно чувствительны к эффектам ковалентности, см. также [98]).

Секулярное уравнение

Для определения коэффициентов с< (t = 1, 2, 3, ... п) используют вариационный принцип (см., например, [33, с. 155]), т. е. условие минимума полной энергии системы в основном состоянии. Предположим, что взаимодействие электронов может быть учтено в виде некоторого эффективного потенциала. Тогда для энергии молекулярной орбиТали имеем

(V.2)

где Й - эффективный одноэлектронный гамильтониан (стр. 16).

Подставляя сюда значение -функции, определяемой пб уравнению (V. 1), и вводя обозначения

можно легко получить следующее равенство:

п п п п

(V. 3) (V.4)

(V.5)

Здесь Sih - интеграл перекрывания орбиталей атомов i и k (см. стр. 28);

при 1фк носит название резонансного интеграла, а Нц - кулоновского интеграла.

Если теперь уравнение (V. б) продифференцировать по с1 и учесть, что согласно условию минимума

- = 0 (/-=1,2.....п) (V. 6)

то легко получим для определения коэффициентов Си следующую систему уравнений:

Z к { ik - EStk) = 0; (i = 1. 2,..., n) (V.7)

Эта система уравнений линейна и однородна. Условием ее разрешимости является равенство нулю детерминанта

\\ffik-ES,\\-0

(V.8)

или в развернутом виде:

Н\\ - EiSii Hi2 - ESi2 ... Нщ- ESin Hii - £21 Нгг - ES22 24 - ESin

Hni - ESni Нп2 - ESn2 ... Hnn~ESni

Условие (V.8) представляет собой уравнение n-й степени относительно Е, которое обычно называют секулярным. В общем случае его решение дает п различных значений Е. Для каждого из них можно получить из системы (V. 7) соответствующий набор коэффициентов ci, сг, сз, с * и, следовательно, соответствующую молекулярную орбиталь (V. 1). Мы получаем, таким образом, для рассматриваемой молекулы п молекулярных орбиталей.

Следовательно, задйча нахождения одноэлектронных молекулярных орбиталей сводится к решению секулярного уравнения (V. 8) и системы уравнений (V. 7). К таким уравнениям приводят все варианты и разновидности метода МО ЛКАО.

V. 2. СВОЙСТВА СИММЕТРИИ МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ

Основные обозначения. Классификация молекулярных термов по симметрии

Значительные упрощения секулярного уравнения метода МО ЛКАО достигаются на основе анализа свойств симметрии с использованием методов теории групп (глава III). Уточним сначала некоторые обозначения. Основные из них приведены на рис. V. 1 - выбор общей и местных систем координат, нумерация лигандов, ориентация их а- и л-орбиталей для октаэдрического и тетраэдрического комплекса. При этом z-оси местных систем на лигандах выбирают направленными к ц. а., что диктуется удобствами вычисления интегралов перекрывания, а остальные оси выбирают произвольно. а-Орбитали лигандов имеют осевую симметрию относительно 2-оси лигандной системы, а л-орбитали расположены в плоскости, перпендикулярной этой оси, с ориентациями вдоль местных х- и -осей. Для спецификации лиганда, к которому относится данная орбиталь, она снабжается соответствующим индексом. Например, nix означает л-функцию лиганда 1, ориентированную параллельно оси х местной системы.

Как показано в разделе III. 4, симметрия системы сразу устанавливает классификацию молекулярных термов по неприводимым представлениям соответствующей точечной группы. Например, для октаэдрического комплекса с одинаковыми лигандами, относящегося к точечной группе симметрии Oh, возможны следующие типы молекулярных термов (в скобках указана кратность

* В силу однородности системы (V. 7) ее решение определяется с точностью до постоянного множителя, который находят затем из условия нормировки.

вырождения терма): Л.!). Л, (1). ЛИ!). 2 (1), Eg (2). Си(2), /ig{3), /iu(3), /2g(3) и T2u{3). Эти типы молекулярных термов существенно ограничивают возможные волновые функции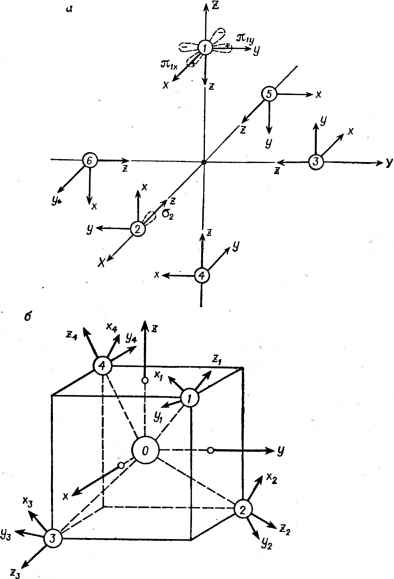

Рис. V. 1. Общая и локальные системы координат для октаэдрического (а) и тетраэдрического (б) комплексов.

соответствующих состояний. Во-первых, число независимых функций, описывающих данный терм, должно быть равным кратности вырождения соответствующего ему типа симметрии, и, во-вторых, эти функции должны обладать надлежащими свойствами симмет-

рии, определяемыми неприводимым представлением этого типа симметрии *.

Для наглядности запишем волновую функцию молекулярной орбитали в виде

¥ = а11)о-1-ЬФ (V.9)

где то - атомная орбиталь центрального атома;

Ф-молекулярная орбиталь системы п лигандов**, равная:

Ф = + Сгфг -f ... -1- СпФп (V. 10)

Здесь i - атомная орбиталь t-ro лиганда, а с, Ь, Ci ..., с - кон? станты, подлежащие определению.

Так как молекулярная орбиталь должна принадлежать к одному из перечисленных выше типов симметрии, то к нему должны относиться, и все члены выражения (V. 9). Другими словами, как г)о, так и Ф должны обладать одинаковыми свойствами симметрии, определяемыми типом симметрии, к которому относится орбиталь. Такие симметризованные линейные комбинации атомных орбиталей, преобразующиеся по определенному типу симметрии группы, получили название групповых орбиталей. Возможные неприводимые представления данной молекулярной системы, или ее тип симметрии определяются по таблицам, аналогичным табл. III. 1 для систем типа Oh (стр. 61).

Построение групповых орбиталей

Для упрощения секулярного уравнения метода МО ЛКАО (V. 8) на основе соображений симметрии необходимо сначала методами теории групп (глава III), во-первых, определить типы симметрии, по которым преобразуются МО, и, во-вторых, построить групповые орбитали -линейные комбинации атомных орбиталей, преобразующихся по данному типу симметрии. Проиллюстрируем применяемые здесь сравнительно несложные методы на примерах.

Рассмотрим октаэдрический комплекс симметрии Oh. В наиболее простом случае а-орбиталей шесть волновых функций лигандов oi, 02, сгб (рис. V. 1,с) при преобразовании симметрии этой группы преобразуются друг через друга, осуществляя некоторое, вообще говоря, приводимое шестимерное представление. Формально это можно записать следующим образом:

а,=сца1 + С12а2+ ... +Ciag ( = 1,2.....6) (V.11)

Таких шесть уравнений необходимо записать для каждого преобразования симметрии группы О/,.

Матрицы этих преобразований, составленные из коэффициентов dj, и образуют искомое представление. Зная эти коэффициенты, можно определить характеры представления - суммы Диагональных элементов каждой матрицы, и затем по формулам,

* Т. е. при преобразованиях симметрии группы Он они должны преобразоваться друг через друга, осуществляя соответствующее неприводимое представление.

** См, примечание на отр. 111.