термы, TigiF) и TigiP), М.ЛС) и M,g(S), более отдалены друг от друга. В предельном случае сильного поля относительно близкими оказываются термы: ig(f2g) и Alg{eg), iT2g(2g) и

? 2g(<2g) (fig) и т. д.

После введения поправок на взаимодействие всех этих пар термов (в общем случае их может оказаться больше, чем по два одинаковой симметрии) мы получаем положение термов, которое не связано с предположением о силе поля лигандов и, следова--тельно, не зависит от того, какой предельный случай был выбран в качестве исходного для анализа.

На рис. IV, 9 показана корреляция термов электронной конфигурации [А] (nd)2 для случаев слабого, сильного и промежуточного полей лигандов октаэдрической симметрии.

Таким образом, для произвольного значения величины энергии поля лигандов картина расщепления зависит не только от параметра поля А, но и от исходного взаимного расположения всех термов, определяемого в соответствии с табл. II. 5 тремя парамет рами Рака А, В и С. Параметр А дает просто одновременное смещение всех -термов (см. табл. II.5, рис. IV.6), зависящее от средней энергии отталкивания между электронами, так что надлежащим выбором начала отсчета энергии его можно исключить (как и среднюю энергию взаимодействия электронов со сферически-симметричной частью поля лигандов Ео). Параметры В и С могут быть определены эмпирически из данных по спектрам свободных атомов и ионов (см. главу II).

В табл. IV. 7 приведены некоторые значения этих параметров и их отношениями у = С/В, которые не очень сильно отличаются между собой (в некоторых случаях для приближенных оценок иногда принимают, что С 4В).

. Таблица IV.7

Некоторые численные значения параметров Рака В и С (в см-) и у = С/В для двух- и трехзарядных ионов переходных металлов [58]

Зная у, можно свести число параметров теории кристаллического поля, характеризующих относительные положения уровней, к двум -А и В. Выбирая, далее, масштаб в единицах В, можно строить диаграммы уровней энергии как функции одного параметра А, наглядно характеризующие электронное строение комплекса и его зависимость от силы поля лигандов.

Подобные диаграммы построены Танабе и Сугано [85; 72, р. 106] для всех конфигураций rf (п = 2, 3, 4, 5, 6, 7, 8) (рис. IV. 10). В них энергия отсчитывается от основного состояния. ]Поэтому, если при каком-то значении А происходит изменение основного состояния (результат пересечения термов), то на диаграмме все уровни испытывают излом. Обычно при этом мультиплет-ность основного состояния меняется и при значении Д (точнее, А/В), при котором появляется излом уровней, происходит переход от слабого поля к сильному.

Диаграммы Танабе - Сугано дают наиболее полную информацию о возможном электронном строении системы в рамках принятых приближений. Усовершенствование таких диаграмм с учетом спин-орбитального взаимодействия см. в работе [86]. (Обзор методов расчета уровней энергии ионов в приближении теории кристаллического поля см. также в монографии [87]).

IVA ОСОБЕННОСТИ РАСЩЕПЛЕНИЯ ТЕРМОВ /-ЭЛЕКТРОНОВ

Отличительные особенности состояний /-электронов например, в комплексах редкоземельных элементов, связанй, прежде всего, с тем, что эти состояния в значительной мере экранированы от поля лигандов внешними s-, р- и rf-электронами, и поэтому меньше подвержены его возмущающему воздействию. С другой стороны, в этих случаях в соответствии с формулой (II. 16) спин-орбитальное взаимодействие значительно больше, чем в случаях rf-электро-нов. Поэтому для /-электронов реализуется особый вариант слабого кристаллического поля, когда оно меньше как межэлектронного взаимодействия, так и спин-орбитального *.

Очевидно, что в этом случае для определения термов атома или иона в кристаллическом поле необходимо исходить из его состояний с учетом межэлектронного и спин-орбитального взаимодействий, 2®+/, которые для каждого терма с данными L и S характеризуются еще квантовыми числами / оператора полного момента количества движения, принимающего все значения от L-f S до jL -S через единицу (стр. 34). При этом, поскольку $ принимает и полуцелые значения, / также может быть полуцелым. Например, состояниями одного /-электрона (L = = 3, S = 1/2) с учетом спин-орбитального взаимодействия будут Л/г и F?, и в приближении обсуждаемого случая слабого поля расщепление каждого из них в кристаллическом поле лигандОв может рассматриваться отдельно.

Распределение электронного облака в состояниях с полным моментом / и расщепление последних под влиянием электростати-

* Бете [69] сравнивает все три вида взаимодействий и рассматривает случаи: приведенного здесь собственно слабого поля; среднего поля, когда взаимодействие с кристаллическим полем меньше межэлектронного, но больше спин-орбитального и сильного поля, когда кристаллическое воздействие больше как межэлектронного, так и спин-орбитального взаимодействий. Для комплексов с а-электронами мы привели варианты слабого и сильного полей, так как первый случай для них реализуется довольно редко,

ческого воздействия лигандов не поддается наглядному толкованию и должно быть рассчитано методами теории возмущений или определено качественно методами теории групп (раздел IV. 2). Однако определенно понимание ситуации может быть достигнуто и здесь при помощи модели чисто орбитальных состояний. Рассмотрение приведенных выше угловых распределений электронного облака /-электронов из кубического набора (табл. II. 2,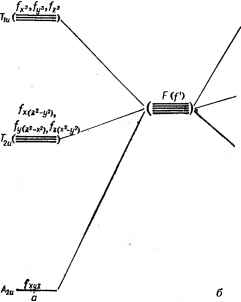

Рис. IV. 11. Иллюстрация к расщеплению орбитальных со-

стояний ском (б

-электрона в октаэдрической (а) и тетраэдриче-полях лигандов (без учета спин-орбитальноо взаимодействия).

рис. II. 2) в поле шести одинаковых лигандов - точечных зарядов или диполей - позволяет легко установить, что наибольшее отталкивание от отрицательно заряженных лигандов испытывает электрон в состояниях fj fy и (причем в одинаковой мере во всех трех)., меньшее -в трех состояниях fy, z r h(z-z) h{x-y-) и еще меньшее - в состоянии fxyz (в тетраэдре картина обратная). Отсюда следует, что семикратно вырожденный орбитально Е-терм свободного атома (или иона) с одним /-электроном в поле октаэдрической симметрии расщепляется на три подуровня, из которых два трехкратно вырождены и один невырожденный (рис. IV. 11).

По аналогии с состояниями d-электронов в кубическом поле, de(eg) и dy{t2g), приводимые выше группы состояний /-электронов называются /в (или t\u), h (или tzu) и /р (или аи) соответственно. Мы получили, следовательно, расщепление: /:->--f Гги-f Лги-

вполне аналогично расщеплению Е-терма конфигурации d, рассмотренного выше (рис. IV. 6 и IV. 7 стр. 81). Однако последовательность расположения уровней здесь обратная случаю в октаэдре (и, кроме этого, все подуровни /-электронов нечетны).

Для иллюстрации приведем также (рис. IV. 12) картину расщепления уровней /-электрона в поле гексагональной бипризмы (с осью 6-го порядка вдоль Oz), реализующейся например, в комплексах уранила [88]. В качестве одноэлектронных были использованы угловые функции из низкосимметричного набора табл. II. 2.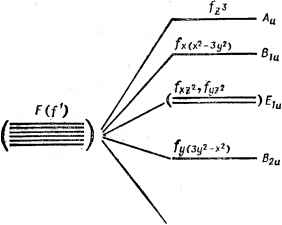

Рис. IV. 12. Расщепление орбитальных состояний f-электрона в поле гексагональной призмы.

Расщепление орбитальных состояний для других случаев симметрии поля лигандов легко находятся по табл. IV. 2.

Количественные расчеты расщеплений термов /-электронов проводятся вполне аналогично случаю d-электронов, рассмотренному выше. Для этого необходимо решить секулярное уравнение типа (IV. 5). Для матричных элементов тт можно ПОЛуЧИТЬ ВЫ-ражения, подобные (IV. 7), для общего случая расположения лигандов- точечных зарядов - в произвольных точках RiRubu Фг) [89]. Однако в отличие от случая d-электронов эти выражения не удалось пока записать единой аналитической формулой для всех матричных элементов с любыми m и т. В табл. IV. 8 они выписаны для каждого матричного элемента в отдельности. Подставляя в них конкретные значения координат лигандов, можно затем подставить их в секулярное уравнение, решения которого суть искомые энергии подуровней расщепления.

2 Таблица IV. 8

Матричные элементы кристаллического поля точечных зарядов, расположенных в точках (Rj, Оу, Фу) ив функциях /-злектронов 3m = R 3lr)Ygt&, ф), т= О, ±1, ±2, ±3. Суммирование производится по всем лигандам,

<01 VI 0> = {f о + (2/15) (3 cos* О/ - 1 )f j + (1/44) (35 cos< - 30 cos* + 3) f + (25/1716) (231 cos* ©у - 315 cos< О/ +

+ 105cos*O/-5)Fe}

<± 1 I V I ± 1) = e* {f о + (I/I0)(3cos*Oy - I)f 2 + (1/264) (35 cos< Oy - 30cos* Oy + 3) f 4 - (25/2288)(231 cos**y - 315 cos* *y-b + 105cos*Oy -5)fe}

<±2 I V I ±2) = e* Po - (7/264) (35 cos* Oy -30 cos* Oy + 3) f 4 + (5/1144) (231 cos dy - 315 cos* Oy + 105 cos* Oy - 5) Fe] I

<±3 IV I ±3> = e* {fo-(I/6)(3cos*Oy - I)f J+(1/88)(35cos* Oy - 30cos*Oy + 3)4 - (5/6864)(231 cOs**y - 315 cos* ©y + + I05cos*dy-5)fe}

<31 F12) = e* (Veyo) exp (- ф) sin * cos {- F + (5/22) (7 cos* 0 - 3) f - (35/1144) (ЗЗ cos* - 30 cos* 0 + 5)

<3 IF i 1> = e* = (V15/2) exp (- Йф) sin* {(-1/15) F + (1/22) (7 cos* - I) f - (35/3432) (33 cos* - 18 cos* 0, +

+1)6}

1F10 = e* J] V5 (7/44)exp (- /3<p,) sin 0, cos {f - (5/26) (II cos* 0 - 3) f J

<31 КI - I) = e* Vl5 (7/88) exp (- 4ф) sin* 0 {(1/3) f - (5/26) (11 совЩ - 1) f J <3Kj-2>=-e* Ve (385/2288) exp (-г5ф)sin5 0 cos*Д

<31 VI - 3) = - e* J] (385/2288) exp (- i6q,j) sin* Of g

(2 I V I - 2> = e* (35/88) exp (- *4ф) sin* 0 {(1/3) F + (3/13) (II cos* д - 1) F}

(I I VI - 1) = - e* exp (- ;2ф) sin* 0 {(1/5) F + (5/66) (7 cos*# - 1) 4 + (175/2288) (33 cos* 0 - 18 cos* в, + l)f J (I I V I 0) = - e* VS exp (- /фу) sin dcos Oy {(1/15) F + (5/132) (7 cos * # - 3) F + (175/3432) (33 cos* Oy - 30 cos* ©y + 5) f J (21 V I 1> = e* VlO exp (- /фу) sin Oy cos Oy {(- l/IO) F - (1/33) (7 cos e - 3) f 4 + (35/2288) (33 cos* dy - 30 cos* + 5) F) (21 F I 0> = e* (V30/6) exp (- /фу) sin* Oy {(- 1/5) F - (1/44) (7 cos* - 1) + (35/572) (33 cos* Oy - 18 cos* dy + 1) f J - <21 VI - 1) = e* VTO (7/44) exp (- /Зфу) sin= dy cos d {(1/3) f 4 + (15/52) (11 cos* d -3)F

CO i