Таким образом, мы найдем, что a(V=:i и aV)=i, а все остальные аР равны нулю. Отсюда следует, что пятикратно вырожденный -терм атомг в кристаллическом поле симметрии Ол расщепляется на два терма: двукратно вырожденный Eg и трехкрат-новырожденный Гг: f f

Таблица IV. 2

Типы симметрии, по которым преобразуются атомные волновые фувкции с данными L (I) или / (/) в различных точечных группах симметрии

Лу 1Тг.° имметрии. по которым преобразуются

функции с 1Ф0, может интерпретироваться как соответствующее расщепление

Таблица IV. 3

Корреляции между типами симметрии групп и и их подгруппами

Совершенно аналогично можно найти расщепление во всех подобных случаях.

В табл. IV.2 приведены типы симметрии (представления), по которым преобразуются сферические функции - орбитали свободного атома в полях различной симметрии, из которой, в частности, виден и характер их расщепления в этих полях. Например, rf-состояния расщепляются в группе Он на Eg и T2g, в группе D3 - на Е, Аи и Е (три компоненты из которых два типа Е), в Dtn - на ig. ig, B2g и Eg и т. д. Аналогичные корреляции между типами симметрии общего характера для некоторых групп и их подгрупп представлены в табл. IV. 3, из которой видно, как расщепляются термы соответствующей симметрии при переходе от группы с более высокой.симметрией к более низкой.

IV.3. НЕСКОЛЬКО (/-ЭЛЕКТРОНОВ

Случай слабого поля

Когда электронная конфигурация центрального иона содержит больше одного rf-электрона поверх замкнутой оболочки, картина возможных термов и их расщепдения в поле лигандов заметно усложняется. Существенную роль в этом случае играет взаимодействие rf-электронов между собой. Если поле лигандов не очень сильное, то атомные термы центрального иона, классифицируемые по квантовому числу полного момента количества движения L, сохраняют смысл, а влияние лигандов можно рассматривать как возмущающее эти термы; в этом случае говорят о слабом поле лигандов *.

Ниже мы сможем дать более точное определение этого термина. Сейчас достаточно подчеркнуть, что под влиянием слабого поля ES-связь между rf-электронами не нарушается и терм с максимальным спином остается основным. Поэтому комплексы со слабым полем называются также высокоспиновыми или спин-свободными.

Основной эффект влияния лигандов, как и в случае электронной конфигурации из одного rf-электрона, -расщепление термов. Но в отличие от варианта rf для нескольких rf-электронов наглядная интерпретация затруднительна. Однако причиной расщепления является тот же эффект, что и для одного rf-электрона: в поле лигандов наименьшей энергией обладают те состояния (многоэлектронные), максимум Ч-функцйй которых простираются в области, отстоящие дальше от лигандов. Рассмотрим как можно трактовать этот случай количественно.

Для электронной конфигурации ц. а. [А] (nd) в поле лигандов, влияние которых слабее межэлектрониого взаимодействия, можно сначала рассмотреть состояние свободного атома, как это сделано в разделе II. 2, и найти его термы, а затем учесть влияние поля

См. примечание к стр. 99.

лигандов на каждый из этих термов в отдельности в виде возмущения. Для двух rf-электронов возможны термы F, P}G, D, S (табл. II. 4), из которых -терм основной. Оператор возмущения двух электронов полем лигандов - точечных зарядов - дается выражением:

Yeq( \ Л- \ \ (IV.24)

Матричные элементы V на функциях (LMSM) двухэлек-тронного терма вычислить сравнительно несложно, если учесть,

что V(r) зависит or координат только одного электрона и не содержит спиновых координат. Поэтому матричный элемент V на функциях ©(mims,; тгШхг) отличен от нуля только для совпадающих у двух функций квантовых чисел ms, и ms, и одного из чисел т (mi или nil):

(Ф(m,m ; m,mJ\v\Ф{m\m,;, т[т[У) = =6,6 . (V ,6 . ,+V ,б ,-V Ь . .-V , .i> \

s, s, s.- sA г l г- 2 l2- 2 ( l , 2 Л rV

(IV. 25)

Здесь Vmm-вычисленный выше одноэлектронный матричный элемент (IV. 7).

На основании этого уравнения легко получить простые выражения для матричных элементов Уц через Vmm, приведенные в Приложении UI.

Для иллюстрации конкретного расчета рассмотрим случай семикратно вырожденного орбитально основного F-терма. Его волновые функции приведены в табл. (II. 8). Секулярное уравнение теории возмущения 7-го порядка для поправок к энергиям уровней имеет вид:

(t. /=1. 2.....7)

(IV. 26)

Для случаев лигандов - точечных зарядов, - расположенных в вершинах октаэдра [с координатами (IV. 9)], отличные от нуля одноэлектронные матричные элементы возмущения Vmm даются выражениями (IV. 11), что в сочетании с соотношениями между Vti и Vmm приведенными в Приложении И1, позволяет получить:

V\2 = Vu = V\e = V\, = = V24 = V = 127 = Vi

Помимо этого

77 22-

Ve И 1/3:

так что уравнение (IV. 26) распадается на более простые, что позволяет получить следующие корни:

2.3=22* IS

4.5.6.7 = Y [(Уп + V33) ± y/iyn-vUf + 4(yUy]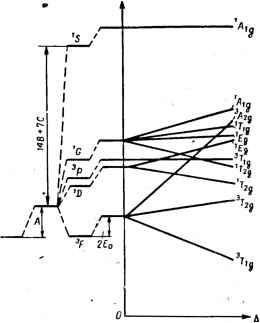

(IV. 27)

Рис. IV. 6. Растепление термов конфигурации d в октаэдрическом поле лигандов - слабое поле:

о-уровень d-электрона; б-сдвиг, вызванный симметричной частью межэлектронного отталкивания; в-расщепление, вызванное межэлектрониым взаимодействием; г-сдвиг, вызванный симметричной частью поля лигандов; в-расщепление в поле лигандов как функция Д.

С учетом значений матричных элементов Vii и выражений (IV. 11) это непосредственно дает (в скобках указаны типы симметрии уровней в группе Oh):

е, iAg) = 200 = eg [12f о + 2f 4].

62. 3,4 [T2g) = Voo + Vn eg [l2Fo +\ ее. ,eTig)==Vo + Vn=eq [12f 0 - F\

(IV. 28)

Или в обозначениях через параметр расщепления кристаллическим полем Д по (IV. 14):

e(M2p = 2£o + -g-A е(Г,) = 2£о-- А

(IV. 29)

Отсюда видно, что трехкратно вырожденный уровень Tig является основным, за ним следует трехкратно вырожденный T2g и затем невырожденный A2g. Расстояние между ними весьма просто зависит от Д и увеличивается с ростом Д, что и демонстрирует рис. IV. 6.

Таблица IV. 4

Волновые функции состояний расщепления Р(й-гбрпа в поле симметрии Од-линейные комбинации функции (LMSMJ) по табл. (II.B) [приведена только компонента с ЛГ = 1, остальные находятся по правилам (11.19)]

В табл. IV. 4 приведены соответствующие этим уровням волновые функции - линейные комбинации функции атомных состояний (LMSMs) (для триплета по спину приведены функции только одного значения спина), определяемые из решения уравнений теории возмущений для коэффициентов Си

Расщепление остальных термов конфигурации [А] (ndY находится совершенно аналогично и приводит к следующим значениям уровней энергии: 2£)-терм

е iEg) = eq[l2fо + F = 2E,+ h

eCTig)=eq

= 2E, -

зр-терм С-терм

e{Tig)=\2eqFo = 2Eo

(IV. 30)

(IV. 31)

eCAig)eq\l2Fo+-F, z(Eg) = eq е(Г,)=е9

e.{Tig)=eq

12fo + ~f4 I2Fo-b-f4j I2Fo-4?-f.

S-терм

8(M,)=:l2e9Fo = 2£o

= 2£o -h-i-A

= 2£o-l-A = 2£o-b-g-A

(IV. 32)

(IV. 33)

Расщепления эти проиллюстрированы на рис. IV. 6.

Здесь как раз уместно выяснить смысл приближения слабого поля и критерий его применимости. Расчеты проведены выше в приближении, в котором теория возмущений применяется к каждому из атомных термов в отдельности. Критерий применимости такого приближения - малость расщепления каждого из термов по сравнению с расстоянием между ними. Как видно из рис. IV. 6, для случая rf2 этот критерий выполняется только при достаточно малых значениях Д. При больших Д компоненты расщепления отдельных термов даже пересекаются, что делает неприменимым приближение слабого поля.

При понижении октаэдрической симметрии оставшиеся вырожденными уровни подвергаются дальнейшему расщеплению. Из табл. IV. 3 (стр. 80) непосредственно вытекает характер этого расщепления.

Можно получить и некоторые количественные соотношения для этих расщеплений. Если кристаллическое поле лигандов - точечных зарядов - имеет симметрию тетрагонально искаженного октаэдра с координатами (Я. II.4), то отличны от нуля те же матричные элементы Vn, что и в случае октаэдра. И, следовательно, корни секулярного уравнения (IV. 26) для расщепления -терма даются теми же общими выражениями (IV.27). Но значения матричных элементов (Я. II.5), а не (IV. 11); это приводит к тому, что пять корней в уравнении (IV. 27) (из которых два корня