центрального атома (ц. а.) можно воспользоваться теорией возмущения. В рассматриваемом случае она приводит ксекуляр-ному уравнению 5-го порядка относительно поправки е к энергии

II mm-efimm11 = О (т. = 2. 1, О, -1. -2) (IV.4)

или подробнее:

= 0 . (IV. 5)

В соответствии с уравнением (IV. 3) матричные элементы возмущения V

(IV. 6)

вычисляются на волновых функциях d-электрона (II. 2). Общее выражение для Vmm получено в Приложении I; оно имеет врд

где Лтт. Втт И Dmm - некоторые коэффициенты. Значения их, определяемые через коэффициенты Клебша - Гордана, приведены в табл.IV. 1

R оо

Fft (R) = I rF (г) dr -Ь /?Ч r-<*+>/? (г) dr (IV. 8)

а функции Fk[R) для известных радиальных функций rf-электрона могут быть получены в аналитическом виде* [см. Приложение I, формула (П1.10)].

Для примера вычислим расщепления терма rf-электрона в октаэдрическом комплексе. В этом случае все лиганды одинаковы и расположены вокруг ц. а. в вершинах октаэдра, так что:

= R{ = R (/ = 1. 2.....6)

dj = ©3 = ©5 = ©e = n/2; 04 = я (IV.9)

<Р2==0; ф8==я/2; <Рб = я; <рв==Зя/2

Подставляя эти значения в выражение (IV. 7) с учетом табл. IV. 1 находим, что V21 = V20 = V2-1 = Vw = = V1-2 =

Не смешивать функции Fi,(R) с параметрами Слэтера - Конлона F пр (П. 32), фигурировавшими в главе 11, Послеяние - просто числа.

:/4яб,

Уо 1 = = V-i-2 = 0 и корни уравнения (IV. 5) получаются непосредственно:

Далее

62 = V22 + V2-2

ва = V22 - V2-2

84, 5 = Vn

V22 = V-2-2 = eg [of о {R)+F, (/?)]

Vn = V-,-i = e<7 [ef 0 (/?) - у 4 ()] Voo = e9l6fo(/?) + f.( )l

V-22 = 12-2= jegF,(R)

(IV. 10)

(IV. 11)

так что

V22 + V2-2 = Voo

V22-V2-2 = Vxi

и различными корнями, будут всего два:

е, = 64 = Voo = eg [6f о (R) + f 4 (/?)! (двукратный)

62 = 88 = 65 = 11=69 e,Fo(R)-Fi(R) (трехкратный)

Таким образом, в соответствии с полученными выше качественными выводами пятикратно вырожденный D-терм в кубическом

(IV. 12)

(IV. 13)

Значения коэффициентов Л , и В , в матричном элементе аозмущеиия -электрона кристаллическим полем (IV. 7).

поле лигандов расщепляется на два терма: Двукратно вырожденный (Eg) и трехкратно вырожденный [Тгд) (рис. IV.2).

Формулы (IV. 10) и (IV. II) позволяют ответить на вопрос, какой из этих уровней лежит выше, и найти величину расщепления между ними Д. Действительно, из выражения (IV. 8) для Fk{R) непосредственно следует, что все Fk>0. Поэтому из двух термов (IV. 13) нижайшим будет трехкратно вырожденный Гг. Величина расщепления равна:

Д = 6 (£) - е (Tg) = у egF, (R)

(IV. 14)

С введением основного параметра теории кристаллического поля Д уровни энергии после расщепления (IV. 13) удобнее переписать следующим образом

e(Eg) = eql6Fo(R) + Fi{R)]

е (Tig)eg

QFo(R)-FiiR)

Eo=&egPD{R)

(IV. 15)

(IV. 16)

Величина £о - средняя энергия отталкивания одного d-элек-трона от шести отрицательных зарядов q при условии, что заряды распределены сферически симметрично вокруг центрального атома на расстоянии

Аналогично проводят расчеты и в других вариантах координации {Приложение II).

По сравнению с октаэдром у тетраэдра расщепление обратное (рис. IV. 3), причем

2 5

е(Г2) = £г + -5-Д, е(£)

eqF,(R)

Fl = 4eqF(R)

(IV. 17)

(IV, 18)

Заметим, что Дт==-д-А, а El = -Eo.

Для кубической координации (8 лигандов в вершинах куба) расщепление качественно такое же, что и в тетраэдре, но в 2 раза больше (рис. IV. 3):

Дк = -е<74(/?) = 2Дх £o=8c?fu(/?)=2£S

(IV. 19)

В случае тетрагонально искаженного октаэдра для описания расщеплений необходимо привлечь помимо А еще два параметра {Приложение II):

Ds = jeq lF2{R2)-F2{Ri)]

(IV. 20)

где Ri и /?2 -расстояния от ц. а. до аксиальных и экваториальных лигандов.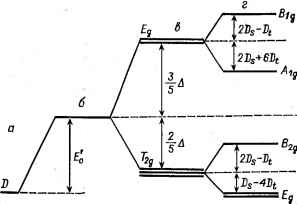

Рис. IV. 5. Соотношение между параметрами расщепления d-уровней D-терма в тетрагонально искаженном (удлиненном) октаэдре и квадрате:

о-свободный ион; б-сферическое поле; в-октаэдрическое полр; г-тетрагонально искаженный октаэдр или квадрат.

С ЭТИМИ параметрами для уровней энергии d-электрона можно получить (рис. IV. 5)

е (Л ,g; rfO = в; + 4 Д - 2Z). - Щ

(IV. 21)

г{E,d ,dy,:)E[--Ds + Щ

Квадрат - это предельно тетрагонально искаженный октаэдр для Rx-*oo. При этом Dt = (2/35) Л, так что для описания расщепления достаточно двух параметров и Л [формула (Я. II. 10)] (рис. IV. 5),

Если лаганд - точечный диполь, то расщепление получается качественно таким же, что и-для зарядов. В предположении, что

длина электрического диполя (с моментом ц) гораздо меньше расстояния до ц. а. величина расщепления, например, для октаэдрического комплекса дается выражением [ср. с уравнением (IV. 14)]

(IV. 22)

где штрих у F означает производную (f 4 < О, так что - f 4 > 0).

При более сложной координации расчеты проводят совершенно аналогично, т. е. сначала по общей формуле (IV. 7) рассчитывают матричные элементы возмущения, а затем решают секулярное уравнение (IV. 5). В случае низкой симметрии (вызванной в том числе и различием в лигандах) последнее решают численно. Варианты трирональной плоской координации, тригональной бипи-рамиды, кубической антипризмы, треугольной призмы и антипризмы и некоторые, другие рассчитаны в работе [75], а семико-ординированный октаэдр-призма симметрии Сг стереохимии 1:4:2 (типа NbF? ) рассмотрен в работе [76].

Теоретико-групповой анализ

Покажем теперь как решается задача о расщеплении вырожденного терма атома под влиянием внешних возмущений посредством методов теории групп без использования секулярного уравнения (IV.5), расчеты по которому зачастую сложны. Воспользуемся для этого результатами главы III.

Группой преобразований симметрии для атома служит группа симметрии шара, обладающая бесконечным числом элементов и множеством неприводимых представлений. Базисными функциями для этих представлений являются сферические функции [см. (II. 2)]

(&, ф) = Р (созв), где - присоединенный полином Лежандра.

Для каждого L имеется 2L + 1 сферических функций с различным М (М = О, ±1, ±2, ±:L), преобразующихся линейно друг через друга при преобразовании симметрии группы и осуществляющих неприводимое представление размерности 2L--1. Атомные термы, следовательно, имеют 2L -f 1-кратное вырождение.

Характеры матрицы представлений группы симметрии шара для поворота на угол ф легко определяются по формуле [69J:

(IV. 23)

При помещении атома в поле симметрии симметрия всей системы становится О и преобразованиями симметрии системы остаются только те, которые соответствуют группе Oh. При уменьшении количества преобразований группы может оказаться, что представление, которое было неприводимым, станет приводимым. Другими слова-ми, если для бесконечного количества преобразований

группы симметрии шара 2L -f- 1 функции базиса не могут быть разделены на группы так, чтобы внутри каждой изних функции преобразовались бы только друг через друга, то для конечного выборочного числа этих преобразований, соответствующих группе Ой, это разделение может оказаться возможным. В этом случае. неприводимое представление группы симметрии шара, которому соответствует один энергетический терм атома кратности вырождения 2L-I-1, для новой группы симметрии Он (соответствующей помещению атома в кристаллическое поле симметрии Он) окажется приводимым. В результате оно распадается на несколько неприводимых представлений (меньшей размерности), которым соответствует несколько энергетических термов (меньшей кратности вырождения), - терм окажется расщепленным.

Для определения вида расщепления необходимо, очевидно, разложить представление группы шара размерности 2L -- 1 на неприводимые представления группы Oh. Эта задача решается полностью при помощи формулы (111.31).

Рассмотрим в качестве примера расщепление D-терма атома, соответствующего L = 2, 2L + 1 = 5, в поле симметрии О/ для которого в предыдущем разделе проведен аналитический расчет.

По формуле (III. 31) нам необходимо знать характеры X(G) представления (приводимого) группы симметрии шара с L = 2 для всех операций G группы Он. Для первых пяти классов эти характеры легко находятся по формуле (IV. 23); для остал11ных пяти - из отмеченного выше условия, что каждый элемент этих классов равен соответствующему элементу из первых пяти классов, умноженному на операцию инверсии. Так как при операции инверсии волновые функции базиса с L = 2 остаются без изменения, то характеры соответствующих матриц будут такими же, как и для первых пяти классов. Например, для элемента Сг, соответствующего повороту на угол п, имеем

sin (2-1-41

s.n-

а для соответствующего элемента 0 = 62 I также Х{аа) = 1, Следовательно, можно получить:

G *£ 6С4 ЗС = ЗС2 8С3 6С2 / 6S4 85б 6а

X{G) 5-1 1 -115-11-11

Теперь при помощи формулы (III. 31) последовательно находим кратность каждого из неприводимых представлений группы Он (см. табл. III. 1) в этом приводимом:

аг = J(5 6 + 3- 8-f6 + 5- 6 + 3- 8-f6) = 0

а( -=-1 = (10-h О-i-6-f 8-h О-j-10-h О-1-6-f 8-h. 10-h 0) = 1

и t. д.