в историческом плане развития теории химической связи теория кристаллического поля в применении к неорганическим комплексам, по существу, может рассматриваться как естественное развитие доквантовых электростатических представлений. Идея электростатической связи между центральным ионом и лигандами впервые была развита Косселем и Магнусом. Электростатические представления основываются на предположении, что центральный ион и лиганды имеют определенные линейные размеры и удерживаются вместе силами ион-ионного или ион-дипольного взаимодействий.

Будучи полезными для своего времени, чисто электростатические представления в дальнейшем не получили существенного развития, так как их неквантовый характер не позволяет объяснить большинство наблюдаемых свойств, обусловленных электронными квантовыми явлениями.

В основе теории кристаллического поля лежат следующие принципиальные положения:

неорганический координационный комплекс существует и устойчив благодаря электростатическому взаимодействию между центральным ионом и лигандами -ионами или диполями;

центральный ион рассматривается с детальным учетом его электронной структуры, а лиганды - бесструктурно - как неизменные источники внешнего электростатического поля (с учетом их возможной поляризации полем центрального иона и остальных лигандов);

описание комплексов зиждется на квантово-механических законах.

Из этих положений в старой доквантовой электростатической теории фигурировало только первое, второе же и третье позволяют рассматривать явления, имеющие квантовую природу, но протекающие главным образом в оболочках центрального иона.

В теории кристаллического поля, таким образом, сама постановка вопроса не позволяет учесть явления, которые обязаны своим происхождением деталям электронной структуры лигандов. Несмотря на эти ограничения (см. подробнее раздел IV.6), теория- в рамках ее применимости - представляет весьма эффективный аппарат исследования строения и свойств координационных соединений.

В соответствии с указанными основными положениями электронное строение комплекса в приближении теории-кристаллического поля находится из решения уравнения Шредингера с гамильтонианом

H = Ho + V (IV.1)

где Но - гамильтониан свободного иона-комплексообразователя; 1 -оператор взаимодействия этого иона с полем лигандов, фиксированных в точках Ri{Ri, ф,) (г = 1, 2, .... Л).

Если воздействие лигандов аппроксимируется полем точечных зарядов qi то V дается выражением

N п

IE

(IV. 2)

рде п -число электронов. Обычно в качестве таковых берутся только валентные электроны центрального иона. Учитывая, что последний заряжен положительно и, следовательно, лиганды отрицательно, мы приходим к выводу, что V по (IV. 2) положительно (qi - абсолютное значение заряда лиганда).

IV.2. РАСЩЕПЛЕНИЕ ТЕРМОВ rf-ЭЛЕКТРОНА

Качественные аспекты теории.Наглядная интерпретация

Теория кристаллического поля приближенно рассматривает неорганический комплекс как устойчивую многоатомную систему, в которой влияние лигандов на центральный ион является чисто электростатическим. Наглядно такой комплекс можно представить состоящим из центрального иона-комплексообразователя, окруженного точечными ионами или диполями, неподвижно закрепленными в некоторых определенных точках (или совершающих малые колебания вблизи этих точек). В такой модели основной эффект комплексообразования должен выражаться в изменении состояний центрального атома при его помещении в поле лигандов. Эти изменения должны нам объяснить все основные физико-химические свойства комплексов.

Задача нахождения атомных состояний под влиянием внешних полей различной симметрии (т. е. различного расположения лигандов) решена Бете [69]. Основной эффект влияния лигандов на состояния центрального иона - расщепление его термов. Происхождение этого расщепления хорошо известно в квантовой механике под названием Штарк-эффекта.

Прежде чем перейти к расчету расщеплений мы предлагаем здесь простую и наглядную интерпретацию этого явления.

Рассмотрим простейший (с точки зрения теории) случай, когда центральный ион октаэдрического комплекса (рис. IV.1,с), например [Т1(Н20)бР+, содержит всего один d-электрон поверх замкнутой оболочки. Основное состояние иона Ti+ - Ю (см. табл. II.5, стр. 35) с орбитальным моментом количества движения L == 2 и полным спином S = V2, т. е. кратностью орбитального вырождения, равной пяти (2L-I- 1 = 5). Пять состояний d-электрона, соответствующих одинаковой энергии системы, описываются в этом случае пятью d-функциями (см. табл. II. 1, стр. 24); их -радиаль-ные части одинаковы. Как было показано (рис. II. 1,в, г, стр. 23), три орбитали dxy, d и dyt, объединяемые пол общим названием de- или <2е-орбиталей, расположены так, что их максимумы попадают в области между осями координат. У остальных двух

орбиталей dz и dx-y (так называемые dy- или eg-орбитали) максимумы расположены как раз вдоль осей. С учетом отрицательного заряда на лигандах (молекулы воды ориентированы отрицательным полюсом диполя к положительному центральному иону) это rf-электронное распределение позволяет получить некоторые качественные выводы об относительном расположении rf-состояний в поле лигандов.

Из сравнения относительного расположения в октаэдрическом комплексе 2g- и eg-орбиталей, например, dxy и dx-y легко видеть, что в состоянии dx-y электрон испытывает большее электростатическое отталкивание от лигандов, расположенных на осях координат, чем в состоянии dxy. По этой причине энергия этих двух состояний не будет одинаковой: в первом состоянии она выше, чем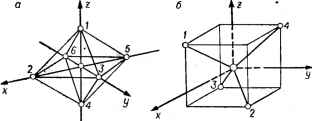

Рис. IV. 1. Нумерация лигандов в октаэдрическом (а) и тетраэдрическом (б) комплексах.

ВО втором. Все три состояния t2g (dxy, dxt и dyz) совершенно симметричны по отношению к шести лигандам, расположенным в вершинах правильного октаэдра, их энергия одинакова и они образуют трехкратно вырожденный терм. Можно показать, что в этом случае и энергия двух eg-состояний также остается одинаковой (см. ниже).

Следовательно, пять d-состояний, обладающих одинаковой энергией в свободном атоме (или ионе), в октаэдрическом поле лигандов разделяются на две группы с различными значениями энергии в каждой. Другими словами, пятикратно вырожденный Ю-терм свободного иона в поле лигандов октаэдрического комплекса расщепляется на два: трехкратно вырожденный T2g и двукратно вырожденный *:

W-g + Eg (IV. 3)

Отметим, что часто приводимые в литературе рисунки расщепления термов, в которых нерасщепленный терм представляется как терм свободного иона, вообще говоря, неправильны. Действительно, при помещении свободного положительного ионе в поле лигандов

* Использованы обозначения Малнкена [68] (см. разделы III. 3 н III. 5); для состояний системы в целом используют большие буквы вместо малых, обозначающих одноэлектронные состояния; в системе с одним rf-электроном одноэлектронные [tag) и полное (Ггв) состояния совпадают.

(например, бтрицательных точечных зарядов) все состояния внешних электронов дестабилизируются из-за дополнительного отталкивания на величину Eo = GeqFo{R) (см. выражение (IV. 16)].

По этой причине картина изменения электронных состояний свободного иона в поле лигандов имеет вид, представленный на рис. IV. 2. Энергия дестабилизации Ео при комплексообразовании компенсируется за счет основной энергии связей, в данном случае- притяжения положительного остова центрального иона и отрицательных лигандов. Эту часть энергии в теории кристаллического поля не рассчитывают и поэтому положение центра тяжести

(=Г=Г)Э(2)

3/5А

D(5) ,

2I5&

Рис. IV. 2. Расщепление атомного D-терма в октаэдрическом поле лигандов:

о-свободный втом; б, в-сферическое и октаэдрическое поля

расщепленных уровней (относительно которого отсчитывается расщепление) остается неопределенным. Легко показать, что он совпадает с положением терма центрального иона в поле заряда лигандов, распределенного сферически симметрично. Вполне определены здесь лишь относительные положения уровней Tje и Eg, энергетическое расстояние между которыми Д называется параметром расщепления кристаллическим полем.

Для тетраэдрического окружения центрального иона (см. рис. IV. 1,6) картина расщепления будет обратной. В этом случае наиболее близкими к лигандам окажутся а- или <2б-орбитали и следовательно, они испытывают большее электростатическое отталкивание, чем eg-орбитали. Поэтому уровни энергии, соответствующие гб-состояниям, лежат выше eg-уровней. Приводимые ниже соображения симметрии и расчет показывают, что в этом случае три состояния <2g и два состояния е§ образуют трехкратно вырожденный терм и двукратно вырожденный терм Е *.

* Индексы *g и ы здесь опущены, так как тетраэдр не имеет центра симметрии и его термы не обладают симметрией {g) или антисимметрией ( ) по отношению к инверсии.

Таким образом, для тетраэдрического комплекса состояния компонентов расщепления D-терма по симметрии будут такими же, как и в случае октаэдрического комплекса, однако взаимное расположение уровней будет перевернутым (рис. IV. 3), т. е. Гг-терм окажется выше С-терма.

Отметим, что дестабилизация терма из-за среднего отталкивания от лигандов в случае тетраэдра меньше, чем для октаэдра [см. уравнение (IV. 18)].

Как октаэдрическая, так и тетраэдрическая симметрии относятся к одной и той же кубической группе симметрии. При понижении симметрии комплекса 6 , термы Т2 н Е подвергаются

} дальнейшему расщеплению. Рассмотрим, например, случай тетрагонального расположения лигандов, образующегося за счет удлинения одной диагонали правильного октаэдра. В этом случае энергии двух eg-состояний {dx-y и rfO уже не будут одинаковыми, так как в первом из них : электрон испытывает более сильное отталкивание от лигандов, чем во втором. Легко видеть, что три состояния t2g также не остаются более полностью симметричными относительно лигандов: два из них - dxz и dyz - одинаково меньше подвержены влиянию лигандов, чем третье - йжу-состояние. В тетрагональном комплексе поэтому D-терм центрального иона расщепляется на четыре терма, из которых только один - Eg, - соответствующий состояниям dxz и dyz, остается двукратно вырожденным (рис.1 V. 4). При дальнейшем понижении симметрии и этот терм расщепляется.

В случае, когда электронная конфигурация центрального иона более сложная, наглядная интерпретация расщепления термов становится затруднительной. Однако когда число d-электронов поверх замкнутой оболочки равно девяти, картина расщепления может получить наглядную интерпретацию, подобную приведенной для случая одного d-электрона. Для этого достаточно принять во внимание, что электронная конфигурация d может быть формально представлена как содержащая одну d-дырку в замкнутой оболочке d (см. принцип дополняющих конфигураций, стр. 43). Ее поведение в поле лигандов совершенно аналогично поведению d-электрона, с той лишь разницей, что в соответствующих членах взаимодействия знаки противоположны (притяжение вместо от-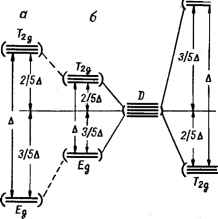

Рис. IV. 3. Расщепление D-терма в кубическом (а), тетраэдрнческом (б) и окта-эдрическом (9) полях лигандов.

талкивания, и наоборот). По этой причине, во-первых, основное состояние электронной конфигурации также является пятикратно вырожденным О-термом и, во-вторых, схема расщепления термов в полях различной симметрии аналогична случаю d (рис. IV.4), однако расположение уровней перевернуто. Это правило взаимного (Соответствия уровней расщепления (с изменением лишь их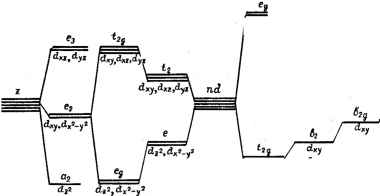

К V Dd Oh Td Oh I!*h

[XkM] [MXg] [MXa] [MX4] [мП [MXg] [MXsY] [MX4Ys1

Икосаэдр Антипризма Kj6 Тетраэдр cqseguwec- Октаэдр

Ш симметрия

----..... --

[MX4]

Плоский транс) квадрат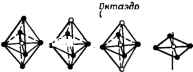

Рис. IV. 4. Расщепление d-орбнталей в полях различной симметрии [74].

взаимного расположения на обратное) сохраняется для любых пар электронных конфигураций d nrfw- (n=l,2,3,4), в которых количества d-электронов и d-дырок в замкнутой оболочке d соответственно одинаковы.

Расчет расщеплений

Количественный расчет расщеплений в теории кристаллического поля не встречает принципиальных трудностей. В рассматриваемом случае свободный атом или ион-комплексообразователь имеют один d-электрон (конфигурация [Л]d, где [Л]--замкнутая оболочка), образующий основной пятикратно вырожденный орби-тально и двукратно по спину терм В поле с потенциалом V этот терм расщепляется.

Предположим, что V значительно меньше внутриатомных взаимодействий. Тогда для расчета влияния лигандов на состояния