Соответствующие этим значениям К\ и /Сз окружно- ги, построенные на комплексной плоскости по ф-лам (1,6), пересекутся в двух точках N я Ni (рис. 6.6). Одна из этих точек будет соответствовать истинному значению комплексного сопротивления Za, а другая - его комплексно-сопряженному значению Zд.

Для определения знака реактивной составляющей измеряемого сопротивления В. И. Бекетовым и А. С. Князевым было предложено включать последовательно с Za дополнительное реактивное сопротивление известного знака. Пусть это дополнительное сопротивление будет емкостью. Тогда при индуктивной реактивной составляющей измеряемого сопротивления последовательная дополнительная емкость Сд переместит точку n (рис. 6.6) в точку М, более близкую к вещественной оси Н1 величину MN=\/(i)Cj, и коэффициент отражения при этом уменьшится, что сразу будет отмечено по уменьшению напряжения в диатонали cd на рис. б.5а [4].

Если же реактивная составляющая измеряемого сопротивления будет иметь емкостный характер, то под-к ючение дополнительной последовательности емкости уместит точку Ai (рис. 6.5) от вещественной оси вниз, в точку Ми что приведет к увеличению коэффициента згражения (увеличению напряжения в диагонали cd).

В принципе, в качестве дополнительной реактивно-:гп может быть взята и индуктивность, но емкость яв-1яется более предпочтительной, так как ее можно вы-юлнить с весьма малыми потерями и небольшой по га-5 ритам.

Указанная дополнительная емкость не должна быть лишком малой, так как при ее большом реактивном опротивлении точка М при измеряемой реактивности -ндуктивного характепа может опуститься значительно иже точки Ni, обусловив тем самым увеличение коэф-ициента отражения и, как следствие этого, ошибку в [тределении знака измеряемого реактивного сопротив-рия.

Гпафоаналитический метод нахождения комплексных противлении г пезультатам двух замепов коэффици-тов бегущей волны напояжения К К дает различаю точность р зависимости от соотношения между венчиками волновых сопротивлений Za < и Zo-; с кото-ыми проводились измерения, и Za.

Рассмотрим, в чем тут дело?

Вследствие noroeuiHOCTefi, завис:чш>их от разлипы) причин, измерение кбв в каждой из линий Zo i . Zn будет проведено с какой-то ошибкой ±АК, поэтому истинное значение кбв окажется ограничено преде-iriM /С(1±Д) и каждому значению кбв на комплексной :ло. скости i X + R будут соответствовать уже некотгоые кольцеобразные области, заключенные между эксценгри-ческими окружностями, определяемыми формулами (1.6), (1.7) при подстановке в них предельных з; 1че-ний: Д (1±А). Координаты конца вектора Za буду находиться в пределах областей взаимных пересечений кольцеобразных зон разброса кбв. Конфигурация этих областей, показанная на рпс. б.бб, зависит как от соотношения величин Zo i и Zo 2, так и от углов, под которыми будут пересекаться окружности.

Относительная погрешность А в из.мерениях кбв для конкретного измерительного прибора в первом приближении является постоянной, поэтому диапазон воз>: к-ных значений кбв можно представить состоящим из последовательности взаимно примыкающих друг к дгугу интервалов шириной 2АК-

В практических условиях сравнительно нетрудно г-су-ществить измерения кбв с относительной погрешностью \ = 0,030,05.

На рис.. 6.7 приведены два графика семейств ок--уж-ностей, определяемых ф-лами (1.6)-41-8) Для послгдо-вательных значений К при А = 0,03 для Zo 2 = 2Z -i (рис. 6.7а) и Zo 2 = 4Zo i (рис. 6.76). Зачерненные к е-лые косоугольные площадки на этих графиках, явл-о-щиеся результатом взаимных пересечений двух семей тв окружностей, в соответствии : изложенными выше г-ловиями их построения дают геометрические места цов вектора Za при трехпроцентной погрешности б мерениях кбв Ki и /С.,

Из графиков рис. 6.7 видно, что на различных у :гках комплексной плоскости площадки погрешнос-ззличным образо.м ориентированы относительнг координат, обусловливая в ряде случаев ппеобл,:::: -щую ошибку лг. одной и? -ставляюшиг. ismepnev гопр :тпгленмя, Рл или В лгстности, при Za. к цем в основном активный характер, весьма замйл i Л лвляется ошибка в определении реактивной составл *-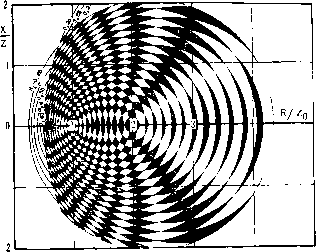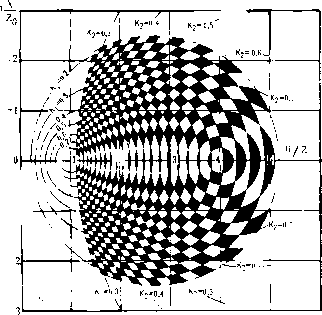

Рис. 6,7