то приходится применять сочетания устройств первой и второй групп.

В ряде случаев улучшение согласо.вания обеспечивают не только подключением к антенне дополнительных устройств, но и подбором излучающих элементов антенн и изменением их конфигурации.

Для пояснения принципа применения последовательных отрезков линий для компенсации Ха обратимся к рис. 1.2. Пусть некая антенна обладает входным сопротивлением, отображаемым точкой 3, и его требуется согласовать с волновым сопротивлением Zq, т. е. требуется переместить точку 3 в точку 5 (Zex = Zo) на вещественной оси.

Подключим к антенне отрезок кабеля такой длины, чтобы точка 3 переместилась в точку 4, у которой Zbx = =Zq-{-[X. Включив теперь последовательную емкость, можно переместиться из 4 .в точку 5 и добиться таким образом требуемого согласования.

Описанная методика согласования является весьма успешной в антеннах, предназначенных в основном для работы на фиксированных частотах. Однако она хорошо иллюстрирует саму идею трансформации сопротивлений.

На практике кривые входных сопротивлений Zbx нередко оказываются смещенными относителыно оси R либо вверх (при больших положительных реактивных составляющих входного сопротивления), либо вниз (при больших отрицательных реактивных составляющих входного сопротивления).

Для компенсации этого смещения достаточно включить последовательно с антенной чисто реактивное сопротивление Апс имеющее противоположный Хх знак. На рис. 1.36,6 показаны при.меры такой ко.\шенсации для Нагрузок с емкостным (рис. 1.36) и с индуктивным (рис. 1.3б) преобладанием.

Частотные зависимости нагрузок до ко.м/пенсации показаны кривыми с точками, рядом с которыми приведены значения относительных частот. Эти нагрузки до компенсации вписываются в окружность кбв для Zo = 76 ом, не превосходящего 0,25.

С целью улучшения согласования в первом случае последовательно с нагруэ :ой нужно включить инЕ-дук-тив1ность, а во втором - емкость. Значения компенсирующих индуктивности и емкости подбираются таким

образом, чтобы результирующая частотная зависимость оказалась расположенной симметрично относительно оси R.

Для этого достаточно определить координату для центра круга ±Л;нкр, ограниченного исходной частотной зависимостью нагрузки, и выбрать величину Хпс таким образОМ, чтобы для средней частоты рабочего диаиазоиа {в нашем примере для f=1.15fo) обеспечивалось равенство

Анкр-Гпс=0. (1.9)

В первом случае A;hi!p = -80 ом, во втором - А;нкр = = +90 ом. Для них соответственно компенсирующие элементы определятся как Xnci = (j:)L, где L = 80/2nX Xl,15fo, гн; со = 2я/ = 6,28/, гц и Хпс2=1/о)С, где С = = l/2jx..l,16fo-90, ф.

Полученные в итоге проведенной компенсации результаты показаны на рис. 1.36, в кривыми с крестиками. Как видно, компенсация существенно улучшила согласования: обе кривые вписываются в окружность фиксированного кбв (/(0,7).

На практике в качестве ко.мпенсирующих элементов не всегда применяют сосредоточенные индуктивности и емкости. Нередко оказывается конструктивно удобно использовать короткозамкнутые или разомкнутые отрезки линии передачи различного волнового сопротивления. При этом результирующая фор1ма кривой входных сопротивлений изменяется тем сильнее, чем меньше волновое сопротивление компенсирующего шлейфа.

Для пояснения более сложных случаев трансформации сопротивлений, а также дальнейших вопросов, связанных с их экспериментальным определением, необходимо предварительно ознакомиться с так называемой круговой номограММой полных сопротивлений.

§ 1.5. Круговая номограмма полных сопхютивлений и правила пользования ею

Полное сопротивление в заданном сечении линии однозначно может быть выражено через параметры коэффициента отражения - его модуль Г и фазу ij: [см. ф-лу (1.1)]. Наиболее наглядно эту связь показывает так называемая круговая номограмма (номограмма

Вольперта), приведенная иа рис. 1.4. На ней нанесены семейства окружностей нормированных значений RIZq и X/Zq. Центры первых окружностей лежат на горизонтальной оси, а центры окружностей фиксированных значений X/Zq лежат на вертикальной оси.

130° f30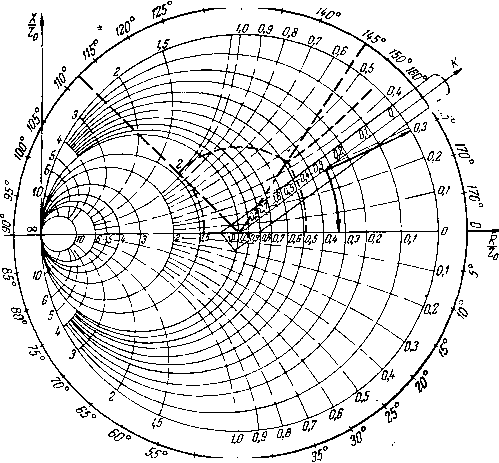

Рис. 1.4

Существует и вторая, связанная с первой, так называемая полярная система координат для коэффициента отражения с центром в точке RIZq=\ (рис. 1.4). В этой системе по азимуту откладывается фаза коэффициента отражения а по рад-иус>-вектору - модуль коэффициента отражения Г. Обе эти координатные системы связаны между собой ф-лой (1.1) и позволяют по за-