x, i = 0x, + 0x, + 0xs+ . . . + lx, + 0u, + 0u,+ . . . +0

где afe=-a +i /ao, =1, n, i=br i/ao, i=l, r.

Введем обозначения: x=[Xi, x2, . . ., XnV -матрица-столбец размера (nXl) переменных состояния, или п-вектор состояния; и=[и Ua, . . ., UrV - матрица-столбец размера (rXl) переменных управления, или г - вектор управления,

- матрица коэффициентов размера (лхл);

- матрица коэффициентов размера (пхг).

-Тогда полученную систему уравнений первого порядка запишем в виде одного векторно-матричного уравнения первого порядка, т. е. в виде уравнения состояния, аналогичного (1.30).

Общее решение уравнения (1.30) представляет собой сумму общего решения соответствующего однородного уравнения х=--Ах и частного решения неоднородного уравнения.

Общее решение однородного уравнения имеет вид x{t) = Q{t) х{0), где Q{t) - матрица размера (пХп), удовлетворяющая уравнению Q=AQ при начальных условиях Q(0) = / (здесь / - единичная матрица).

Матрицу Q{t) называют фундаментальной матрицей уравнения (1.30).

Она имеет вид Q(t)=et, где е = I+At+. . .+-A t+. .

матричная экспонента.

Частное решение неоднородного уравнения (1.30) может быть выражено через фундаментальную матрицу и представлено в виде многомерной (матричной) свертки:

x{t) = Q{t) 5 Q-i(T)Su(T)aT=: {Q{t)Q-{x)Bu{x)dx =

= 5 e-4 c--) Bu (T) dr = 5 /г (t-x) и (т) dx,

тле. h{t)=e*B - матрица весовых функций размера (яХг) автоматической системы, описываемой уравнением (1.30).

На основании теоремы об изображении свертки получаем Х{р) = =Я(р) и(р), где Х{р) к и (р) ~ соответственно матрицы изображений переменных состояния и переменных управления; Н (р) ~ матрица передаточных функций автоматической системы, определяемая как изображение матрицы весовых функций.

Использование частотных передаточных функци.1. Частотные методы исследования автоматических систем основаны на рассмотрении установившейся/реакции системы на гармоническое входное воздействие.

Частотные передаточные функции используются главным образом в задачах анализа автоматических систем. Для решения задач синтеза более удобен и получил широкое распространение метод логарифмических частотных характеристик.

Пусть дано дифференциальное уравнение динамической системы [см. (1.3)]. Рассмотрим установившуюся реакцию этой системы на гармоническое входное воздействие, которое. запишем в комплексной форме:

л:l(0 = l .e< * = л:г.e/ (1.31)

где Xjrn- амплитуда гармонических колебаний; со - круговая частота колебаний; t3i- начальная фаза колебаний; Xim-Xim- комплексная амплитуда колебаний.

Будем искать частное решение неоднородного уравнения (1.3) при нулевых начальных условиях в виде

2 ii) = x2d ( +* =2 е (1.32)

Подставляя (1.31) и (1.32) в (1.3) и учитывая, что

получим где

x, = W{h)x

частотная передаточная функция динамической системы, описываемой дифференциальным уравнением (1.3).

Как следует из (1.33), частотная передаточная функция является дробно-рациональной функцией переменной /ш.

Сравнивая (1.33) и (1.16), видим, что частотная передаточная функция может быть формально получена из передаточной функции путем подстановки /?=/м.

Частотная передаточная функция есть комплексная функция переменной ш и, как всякая комплексная функция, может быть представлена в одной из форм:

Г (/ш) = (/(©) +/У (ш) (1.34)

W (/щ) = I W (/ш) I е/ = А (ш) е* < >, (1.35)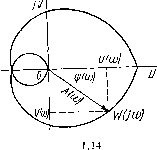

Рис.

где и (а) - вещественная часть функции W{j(xi); V(co) - мнимая часть функции W(j(>)); Л (со) = 1У(/сй) - модуль функции i5(co) = arg W(j(i>) - аргумент функции W(](!)) или фаза.

Модуль частотной передаточной функции динамической системы определяет амплитудно-частотную характеристику (АЧХ) этой системы, а аргумент-фазо-частотную характеристику (ФЧХ).

Частотная передаточная функция является вектор-функцией и графически изображается на комплексной плоскости в виде вектора с прямоугольными координатами t/(cu) и V {&) или с полярными координатами А (со) и г5(сй), как показано на рис. 1.14. При изменении переменной со в пределах (- -f-oo) конец вектора описывает кривую, которую называют амплитудно-фазовой характеристикой системы (АФХ).

Из рис. 1.14 может быть найдена связь между вещественной и мнимой частями функции 1(/со), с одной стороны, и модулем и аргументом - с другой:

А (со) = 1/ (/а (co)-f Ксо), г, (со) = arctg

(1.36)

f/ (со) = Л (со) созг) (со), К (со) = Л (со) sin ф (со).

Вещественная часть функции IF (/со) есть четная функция переменной со, а мнимая часть - нечетная функция. Действительно, запишем (1.33) в виде

W (/со) = Rmih) Dn(-M = f/ (со) 4- ,у (ш).

1> (/со) (-/со) I Otv(/ш) I + i

Знаменатель этого выражения, общий для f/(co) и К(со), представляет собой квадрат модуля функции Djv(/co) и содержит лишь четные степени со. Следовательно, мнимая и вещественная части частотной передаточной функции IF (/со) выделяются в числителе. Но при умножении полиномов RmH) и Djsr{-/со) вещественная часть произведения содержит лишь четные степени со, а мнимая часть - лишь нечетные. Таким образом, числитель и знаменатель функции U(со) содержат лишь четные степени со и тогда U{-со) = [7(со), в то время как числитель функции К (со) содержит лишь нечетные степени со, а знаменатель- четные, и тогда V{-со)=-К(со). Отсюда также следует, что модуль А (со) = VU (со) + (со)- четная функция, т.е. Л (-со)=Л (со), а фаза (со) = arctg-j- - нечггная функция, т.е. г)(-со)=-г)(со).

Поэтому АФХ динамической системы представляет собой кривую, симметричную относительно оси абсцисс, так как каждой точке АФХ с координатами [f/(co), V(a)] или [Л (со), г)(со)] соответствует ее зеркальное отражение в оси абсцисс с координатами [f/(-со), V{-со)] = = [f/(co), -У{а)] или [Л (-со), г)(-со)]=[Л (со), -ф(со)]. Соответственно АЧХ системы си.м,метрична относительно оси ординат, а ФЧ X симметрична относительно начала координат.

2 Зак. 561 33